1. 引言
我国已经成为世界第一大产销大国,随着电商以及快递业务的增长,作为公路货运主要承担者的货车仍然扮演着重要作用 [1] 。车辆行驶过程中,车架不仅要承受各种载荷与力矩,还不停地受到来自汽车动力系统、传动系统以及路面激励而产生的振动,这就对车架本身的刚度和强度以及振动特性提出了较高的要求。车架设计是整车开发过程中十分重要的一环,随着新材料、新工艺、新结构等方法的发展,车架开发方法也在不断的进步,各厂家都相继开发出性能优质量轻的车架 [2] 。结构方面,西方发达国家真正在汽车结构轻量化方面取得重大成果是在上世纪七十年代以后,这主要得益于当时力学、计算机以及数值计算等基础学科的飞速发展,其中数值计算的方法包括有限元法、边界元法以及有限差分法等。在机械以及汽车领域逐渐形成了以数值计算为基础的结构分析与优化技术。有限元分析已经被广泛应用于结构刚强度分析 [3] 、碰撞分析 [4] 、NVH分析 [5] 、优化分析等。
2. 车架有限元模型建立
车架有限元模型的建立是前期处理工作,主要涉及到以下几个方面:一是模型的导入,二是网格划分,三是定义车架各部件材料和属性,四是建立各部件之间的连接关系,五是边界条件的设置等,以下针对有限元建模过程中的一些关键步骤及关键设置进行相关阐述。
首先是模型的导入,车架A和车架B都是边梁式车架,二者横梁及纵梁总数量相同,但是布置位置有所差异,车架A第二横梁分为上下梁,车架B第二横梁为圆管梁。该车架各部件由焊接和螺栓连接两种连接方式装配,在进行车架强度及模态的有限元分析时,主要关注纵梁及横梁等部件上的应力、固有频率及振型,不需要关注焊缝、螺栓等细节部位,故可以采用RB2单元刚性连接车架各钣金件,将两个钣金件的螺栓孔(或者焊点)通过Washer操作将圆孔外扩,再通过RB2单元连接成蜘蛛网结构,建立好的车架A及车架B有限元模型分别如图1和图2所示。车架的主要参数如表1所示。

Table 1. Main parameters of the frame
表1. 车架主要参数
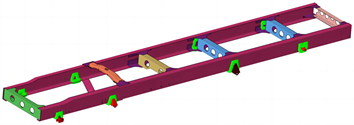
Figure 1. Finite element model of frame A
图1. 车架A有限元模型
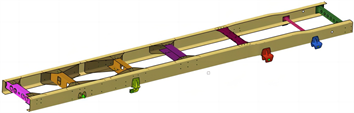
Figure 2. Finite element model of frame B
图2. 车架B有限元模型
材料设置:在划分网格之前先测量各部件厚度,用于后续给各部件网格附上相应厚度,车架所用材料的弹性模量为2.1E5 MPa,密度为7.85E−6 kg/mm3,泊松比为0.3,相关板厚参数如表2所示。

Table 2. Two car plate thickness parameters
表2. 两款车板厚参数
网格划分:车架A的网格数量为259,263,节点数为264,767,最小网格尺寸为1.4 mm,最大尺寸为9.4 mm;车架B的网格数量为326,418,节点数为331,507,最小网格尺寸为1.9 mm,最大尺寸为11 mm。
边界条件设置如下:1) 模态分析为自由模态分析,是结构的自然属性,在此不设置任何边界条件;2) 静强度校核根据车辆实际使用情况(极限工况)来设置,主要包括满载工况、紧急制动工况、最大侧向力工况以及扭转工况,结合整车使用情况,考察车架的应力分布情况,确保车架最大应力在车辆任何极限工况下均能低于材料屈服强度,保证车辆行驶安全;3) 刚度校核主要包括弯曲刚度和扭转刚度,根据实际情况对车架进行约束,考查车架不同工况下抵抗变形的能力。
3. 车架模态分析以及强度分析
3.1. 车架模态分析
模态特性是车架的固有属性 [6] ,任一阶次模态的频率、振型与其受力情况都没关系,因此对车架自由模态分析时,不需要施加任何约束条件或载荷。其中车架的1~6阶模态固有频率都接近0,接近刚体模态,在此忽略不计,认为第7阶弹性模态为车架的一阶模态。
求解车架的前六阶模态,在Hyperview软件中查看求解结果,车架A及车架B各阶模态固有频率及振型描述如表3所示,车架B的一阶模态频率高于车架A,侧面反映车架B的一阶扭转刚度大于车架A。车架B的一、四阶模态频率高于车架A,其余模态频率低于车架A,两车架的前5阶模态振型一致。

Table 3. Natural frequency and vibration mode of the frame mode
表3. 车架模态固有频率及振型
3.2. 车架强度分析
车架在车辆运行过程中,承受路面以及发动机的各种交变载荷,受力是十分复杂的 [7] 。本文主要在下面四种工况进行车架的静力有限元计算。
1) 满载载荷计算
满载工况下,车架的主要外力来源于以上部件及货物的重力,此外还承受车架自身的重力,车架受载质量类别如表4所示。

Table 4. Load capacity of the frame
表4. 车架受载质量
2) 紧急制动工况加速度计算
车辆最大制动力,取决于制动器制动力以及地面制动力,制动力的大小取决于二者之中较小值 [8] 。货车由于质量较大,制动时会出现车轮抱死现象,因此选取车轮制动抱死滑拖时的制动力作为最大制动力分析工况输入,此时车轮最大制动力为:
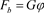 (1)
(1)
为车轮附着系数,通常取
;
故取最大制动加速度为0.8 g。
3) 紧急转弯工况加速度计算
车辆由于转向或者路面不平,车辆会受到侧向力。当所受侧向力超过车辆轮胎所能提供的最大侧向力时,车辆则会产生侧滑。车辆发生侧滑的条件为 [9] :
车辆驱动桥侧滑的条件是,
(2)
为驱动桥受到的侧向力;
轮胎所能提供的最大侧向力。
(3)
为轮胎侧向附着系数,通常取1.0
故取最大侧向加速度为1 g。
4) 扭转工况载荷计算
扭转工况所受的载荷于满载时基本一致,只是由于车轮陷落,而是车架发生扭曲变形,车架受力增大 [10] 。
3.3. 两种工况结果分析
本文分别将车架A和车架B在最大侧向力工况和扭转工况下进行有限元模型求解,其中最大侧向工况约束如下:左前轮心约束三个方向平动自由度,左后轮心约束侧向和垂向平动自由度,右前轮心约束纵向和垂向平动自由度,右后轮心约束垂向平动自由度。扭转工况约束如下:左前轮心约束三个方向平动自由度,左后轮心约束侧向和垂向平动自由度,右前轮心约束纵向和垂向平动自由度,右后轮心释放所以自由度。
1) 最大侧向力工况分析结果:根据计算结果得到两款车架的紧急制动工况位移云图分别如图3和图4所示,应力分布云图分别如图5和图6所示。由图3和图4可得,最大侧向力工况下车架A最大变形量为1.1 mm,车架B最大变形量为7.1 mm,根据文献 [11] 要求,货车车架最大弯曲挠度通常小于10 mm,车架B变形量已经与该标准接近。由图5和图6可得,车架A最大发生在后板簧安装支架与纵梁连接处,最大米塞斯应力为193 MPa,低于材料屈服强度;车架B最大应力为879 MPa,高于材料屈服强度,故该工况下车架A强度设计合理,车架B强度设计不合理。最大侧向力工况下车架B的最大应力部位位于第二横梁与纵梁连接部位,该部位米塞斯应力为879 MPa,超出材料屈服强度。另外,后板簧安装支架(后)的连接板与圆柱相接部位米塞斯应力为810 MPa,也超出材料屈服强度,故车架这两个部位设计安全强度不合理,存在较大风险,需对这两个部位进行优化。
2) 扭转工况分析结果:根据得到两款车架的扭转工况位移云图分别如图7和图8所示,应力分布云图分别如图9和图10所示。
由图7和图8可得,扭转工况下车架A最大变形量为2.0 mm,车架B最大变形量为2.0 mm,根据文献 [11] 要求,货车车架最大弯曲挠度通常小于10 mm,满足设计要求。由图9和图10可得,车架A最大应力发生在第二横梁上梁与纵梁交接处,最大米塞斯应力为366 MPa;车架B最大应力发生在第三横梁与纵梁交接处,最大米塞斯应力为200 MPa,均小于材料屈服强度,该工况下车架强度设计合理。
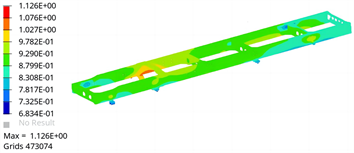
Figure 3. Maximum lateral force working condition displacement of frame A
图3. 车架A最大侧向力工况位移
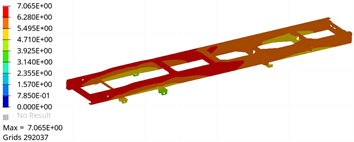
Figure 4. Maximum lateral force working condition displacement of frame B
图4. 车架B最大侧向力工况位移

Figure 5. Stress distribution under maximum lateral force condition of frame A
图5. 车架A最大侧向力工况应力分布

Figure 6. Stress distribution under maximum lateral force condition of frame B
图6. 车架B最大侧向力工况应力分布

Figure 7. Frame A torsion condition displacement
图7. 车架A扭转工况位移
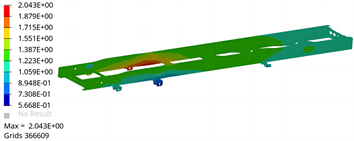
Figure 8. Frame B torsion condition displacement
图8. 车架B扭转工况位移

Figure 9. Stress distribution under torsional working condition of frame A
图9. 车架A扭转工况应力分布

Figure 10. Stress distribution under torsional working condition of frame B
图10. 车架B扭转工况应力分布
4. 车架刚度分析以及改进方案
4.1. 刚度分析
为了保证货车在行驶过程中不会因车架的弯曲变形而导致装配在车架上的零部件发生相对位移从而导致零部件的损坏或者提前失效,车架应具有足够的弯曲及扭转刚度。
1) 弯曲刚度计算
将车架总成简化成一根简支梁结构,约束梁两端的垂向位移,并在梁中心处施加一竖直向下的载荷,使之产生形变 [12] 。
车架弯曲刚度计算公式为:
(4)
式中,
代表集中载荷,单位为N;a代表轴距,单位为m;
代表挠度,单位为m。弯曲刚度另外一种常见的计算公式为:
(5)
式中
,为加载点的垂向位移。
相比较第一种表达式,第二种表达式更加简单直观,工程上通常采用第二种弯曲刚度表达式。
2) 扭转刚度计算
将车架简化为四边形结构,约束四边形的A、B两处垂向位移,在C、D处施加一对竖直方向上方向相反的力,示意图如图11所示。
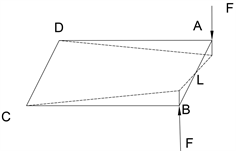
Figure 11. Schematic diagram for calculating the torsional stiffness of the frame
图11. 车架扭转刚度计算示意图
扭转刚度计算公式为:
(6)
式中,Kt为扭转刚度,单位为Nm/˚;T为力矩;
为扭转角。
由于扭转角与扭转力矩间呈线性关系,故对扭转载荷值的选择无关紧要,但通常扭转试验载荷取为3000 N∙m,这样既能保证试验结果的精确性,又可避免因试件超过弹性极限而产生误差 [13] 。
4.2. 刚度改进方案
4.2.1. 车架A改进方案
经计算发现车架A的弯曲刚度与车架B相当,但扭转刚度远小于车架B,如果车辆在行驶过程中车架变形过大,则会导致车架寿命缩短,同时也对其他零部件寿命不利,不利于车辆的安全行驶,故要对车架A的扭转刚度进行改进。
经对比,车架B的第二横梁位置比车架A第二横梁的位置更靠前,该结构对车架扭转刚度有利,但车架各梁位置是固定的,不宜更改,仅能从各零部件厚度角度改进。车架A最大变形位置位于车架前端,故有限对车架A前部横梁或支架进行改进,根据表2分别将车架A的第一横梁、第二横梁上梁、第二横梁下梁、前板簧前安装支架以及第三横梁安装支架分别增加10%厚度(调整一个零部件厚度时,其他零部件厚度调整),并计算结果,获得车架扭转刚度对各个零部件厚度的敏感性,扭转刚度在此以位移变化率来描述。
车架A的第二梁下梁变化对车架A的扭转刚度影响最大,第三横梁其次,其他几个零部件厚度变化对车架A扭转刚度几乎没有影响,故在此对第二横梁和第三横梁进行改进,将第二横梁厚度由8 mm增加到14 mm,第三横梁厚度由8 mm增加到12 mm。
按上述方案修改车架A有限元模型(扭转刚度模型),修改后重新求解该有限元模型,计算获得改进后车架A的最大变形量为57.5 mm,比改进前最大变形量72.4 mm降低了21%,车架扭转刚度由728.4Nm/˚提升为833.3 Nm/˚,扭转刚度提升了14.4%,改进后位移云图如图12所示。

Figure12. Improved frame A torsional stiffness displacement cloud map
图12. 改进后车架A扭转刚度位移云图
此外,由于车架A结构与车架B结构不同,车架B的第二横梁与车架前端更为接近,使车架B的扭转刚度大大提升,由于车架受整车总布置影响,故在此只能对板厚进行优化,但板厚也不能无限制加厚,故在此只能对扭转刚度进行适当改进。
4.2.2. 车架B改进方案
第三章车架静强度计算最大侧向力工况显示车架B在该工况下第二横梁与纵梁连接部位米塞斯应力达到879 MPa,后板簧后安装支架的连接板与圆柱相接部位米塞斯应力达到810 MPa,均超出了材料屈服强度,车架B的这两个部位设计安全裕度不合理,存在较大风险,需对这两个部位进行改进。
第二横梁为平板接头与圆管的焊接件,最大应力发生在连接板的安装孔周围,故初步判断可将连接板厚度加厚,连接板原厚度为6 mm,初步将其加厚至8 mm。
按改进方案修改车架B有限元模型(最大侧向力工况),修改后重新求解该有限元模型,计算获得改进后车架B的最大变形量为5.3 mm,比改进前最大变形量7 mm降低了24%,改进后位移云图如图13所示;最大米塞斯应力为560 MPa,比改进前最大米塞斯应力879 MPa降低了36%,改进后应力分布云图如图14所示。
5. 总结
本文通过有限元方法对两款货车车架分别进行了模态分析、静强度分析以及刚度分析,找出了车架设计的薄弱环节,并通过对结构的改进使得车架设计符合要求。具体内容如下:1) 基于两款已有货车车架,

Figure 13. Displacement diagram of improved frame B
图13. 改进后车架B位移图
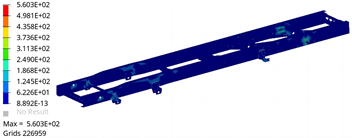
Figure 14. Maximum lateral force working condition stress cloud map of improved frame B
图14.改进后车架B最大侧向力工况应力云图
分别建立了两款车架的有限元模型,其中介绍了常规有限元建模方法;2) 对两款车架进行了模态分析,并分别计算了前六阶模态频率及模态振型;3) 基于四种工况对两款车架进行了强度分析,仿真了两种工况,计算结果表明车架A结构强度满足设计要求,而车架B在最大侧倾工况下最大应力超出材料屈服强度,不满足强度设计要求,计算结果为后续车架优化提供依据;4) 介绍了车架弯曲刚度及扭转刚度的计算方法,并基于此方法对两款车架进行了弯曲刚度及扭转刚度计算。5) 根据静强度分析结果分析了车架B局部应力过高的原因,根据刚度分析结果分析了车架A扭转刚度较低的原因,并分别给出了改进方案,基于最大侧倾力工况及扭转工况有限元模型求解,验证了两款车架的改进效果,经验证改进结果合理。