1. 引言
1.1. 研究背景及现状
自从二十世纪六十年代以来,图论已经成为发展迅速的数学分支之一,图论的很多理论在解决运筹学,化学,生物学,网络理论,博奕论等学科问题中起着非常重要的作用。它作为组合数学的一个分支受到了各个方向的普遍重视。
图的哈密顿问题便是其中一个比较重要的研究主题,哈密尔顿图是以爱尔兰著名数学家William·Hamilton的名字所命名的。他是第一个给出复数的代数(而非几何)描述的人,并且他于19世纪所发明的Icosian的游戏正是哈密尔顿图的前身,哈密尔顿图作为图论的一个重要分支和其它图理论问题有着非常紧密的联系,Hamilton问题是从所谓的“周游世界问题”的游戏中提出来的 [1] 。1856年著名的爱尔兰数学家William·Hamilton (1805~1865)设计了一个游戏:给定世界上20个城市,从某一顶点出发,沿着十二面体的棱,经过每个顶点恰好1次,最后回到出发点 [2] 。
1998年Fisher,McKenna和Boyer [3] 研究了图G的Mycielski图
的哈密尔顿性质,并得出了以下结论:
定理1.1(Fisher [3] )以下是关于图G的相关结论:
(1) 设G是哈密尔顿图,则
也是哈密尔顿图;
(2) 设G不是连通的,则
不是哈密尔顿图;
(3) 设G是至少含有两个悬挂点的图,则
不是哈密尔顿图。
2017年Jarnicki,Myrvold,Saltzman和Wagon [3] 进一步研究了一般图G及其Mycielski图之间的关系,并得到了以下结论:
定理1.2 (Jarnicki, Myrvold, Saltzman, Wagon [3] )图G具有如下结论:
(1) 如果图G是一个奇圈,那么
是哈密尔顿连通的;
(2) 如果图G是阶数为奇数的哈密尔顿连通图,那么
是哈密尔顿连通的;
(3) 如果图G是一个偶圈,那么
不是哈密尔顿连通的。
1.2. 基本概念
本论文只研究有限简单图。一个图称为简单图,如果它既没有自环也没有两条边连接同一对顶点。设
是一个简单图,
是图G的顶点集,顶点数
称为图G的阶数,
是图G的边集,边数
称为图G的大小。一般地,把由顶点u和v组成的边记为
或者
。图G中顶点v的度是指与v相关联的边数,记为
或
,度为0的顶点称为孤立点,度为1的顶点称为悬挂点。我们用
记为G的最小度,即
,用
记为G的最大度,即
。
称图H是图G的子图(记为
),如果
,并且对于每一条边
,u,v都在顶点集
中。也就是说,图H可以通过删除图G中的一些顶点或一些边获得。图G的生成子图是指满足
的子图H。
包含G的每个顶点的路称为G的哈密尔顿路;类似地,G的哈密尔顿圈是指包含G的每个顶点的圈。图G称为哈密尔顿连通当G满足,对任意一对顶点x,y,G中都存在从x出发到y的哈密尔顿路。
图G的顶点集记为
,它的Mycielski图记为
,
的顶点集为
,边集为z所有的
相邻,以及
,当
。令
,构造
的Mycielski图得到
,由此重复选代可以得到
。这样得到的图称为Mycielski图
。
是色数为n的不含三角形且顶点数较少的图。
对于上述概念和术语可以参考 [2] [4] [5] 。
1.3. 本文主要工作
本文研究了一些具有哈密尔顿性质的特殊图类,这些图的Mycielski图均具有哈密尔顿连通性质。
在本文中,我们主要得到一下结果。
定理1.3 设图G是哈密尔顿连通图,如果对任意的
,存在由v开始的Mycielski因子,则
是哈密尔顿连通的。
定理1.4 设图G是阶数
的哈密尔顿连通图,如果
,则
是哈密尔顿连通的。
2. 主要结果
简单回忆哈密尔顿连通的定义:图G中,任意一对顶点
在G中都存在从x出发到y结束的哈密尔顿路。
在证明下述定理之前,首先我们定义Mycielski因子如下:
定义2.1 设图G是阶数为偶数的n阶连通图,
。称图G的连通生成子图为Mycielski因子当且仅当中有一条从
出发的路,该路包含个数为偶数的奇圈
(可能n = 0)和含有一条偶长弦的偶圈
(可能不存在),这些圈由2s条边
连接,
,
使得
,
,偶圈的弦连接
和
上的一点使得该弦的距离为偶长。
定理2.2 设图G是哈密尔顿连通图,如果对任意的
,存在由v开始的Mycielski因子,则
是哈密尔顿连通的。
证明:设图G是哈密尔顿连通的。由定理1.7 (2)可知,图G的顶点数为奇数时
也是哈密尔顿连通。故只需考虑当图G的顶点数为偶数时的情形。令
,
。任取两点
分别讨论
在
中不同位置时的情况,并证明。
(i)
。
当
时,由于图G是哈密尔顿连通的,因此在图G中存在一条路P,其中P的起点为
,终点为
,故在
中存在一条哈密尔顿路
。记作:
,
如图1所示。

Figure 1. Hamilton road from u to v (1)
图1. u到v的哈密尔顿路(1)
(ii)
。
当
时,由于图G是哈密尔顿连通的,因此在图G中存在一条路P,其中P的起点为
,终点为
,故在
中存在一条哈密尔顿路
。记作:
,
如图2所示。
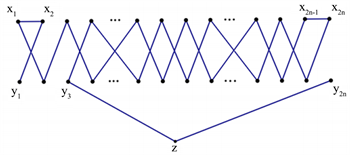
Figure 2. Hamilton road from u to v (2)
图2. u到v的哈密尔顿路(2)
(iii)
。
当
时,由于图G是哈密尔顿连通的,因此在图G中存在一条路P,其中P的起点为
,终点为
,故在
中存在一条哈密尔顿路
。记作:
,
如图3所示。

Figure 3. Hamilton road from u to v (3)
图3. u到v的哈密尔顿路(3)
(iv)
。
当
时,由于图G是哈密尔顿连通的,因此在图G中存在一条路P,其中P的起点为
,终点为
,故在
中存在一条哈密尔顿路
。记作:
,
如图4所示。

Figure 4. Hamilton road from u to v (4)
图4. u到v的哈密尔顿路(4)
(v)
。
令
,图G中有一条从
出发的路,该路包含个数为偶数的奇圈
(可能n = 0)这些圈由2s条边
连接,和含有一条偶长弦的偶圈
(可能不存在),偶长弦连接
和
上的一点,若
,对任意
,给
的顶点顺时针排序为
。因此在
中有如下的哈密尔顿路
:
,其中
。
令含有偶长弦的偶圈
,其中偶长弦为
,因为可以在
中找到如下哈密尔顿路
:
,
.
如此便可得到
中从
出发到z的哈密尔顿路:
如此完成了证明 [3] [6] 。
定理2.3 设图G是阶数
的哈密尔顿连通图,如果
,则
是哈密尔顿连通的。
证明:因为图G是哈密尔顿连通的,故图G有哈密尔顿圈C。u是圈C上的一点,因为
,所以圈C上有距离u为偶数的邻点。由定理2.2可得,
也是哈密尔顿连通的。