机器学习识别六方伊辛晶格中的相位和相变

Phases and Phase Transitions in Hexagonal Ising Lattices Identified by Machine Learning

摘要: 机器学习可以在对系统潜在特性缺乏先验知识的情况下，识别数据中的模式并发现物理系统的性质和物理量。在本文中，我们使用非监督机器学习技术——主成分分析(Principal Component Analysis, PCA)方法识别六方伊辛晶格的相和相变。研究表明，PCA可以成功识别六方伊辛晶格的相变并定位相变临界温度。此外，通过PCA所获得的第一和第二主成分还可用于确定晶格的磁化强度和磁化率。

Abstract: Machine learning can identify patterns in data and discover the properties and physical quantities of physical systems without prior knowledge of the system’s latent characteristics. In this paper, we employ unsupervised machine learning techniques—specifically, Principal Component Analysis (PCA)—to identify the phases and phase transitions of the hexagonal Ising lattice. Our study demonstrates that PCA can successfully identify the phase transitions of the hexagonal Ising lattice and locate the critical temperature of these transitions. Furthermore, the first and second principal components obtained through PCA can also be used to determine the lattice's magnetization and susceptibility.

1. 引言

机器学习，凭借其在缺乏物理先验知识背景下对复杂物理系统进行剖析的能力，已成为探究物理学知识的一项有效工具。借助机器学习，即便在未知物理系统哈密顿量的条件下，也能洞察其行为模式。机器学习赋予计算机从各种经历、事件或数据中学习与推理的能力，以在不明了问题先验知识的情况下寻求解决方案。通过运用多样化的监督与非监督学习策略，机器学习技术在物理科学领域引发了革命性的进展，诸如晶体结构的预测 [1] 、密度函数的近似 [2] 、分子能量的模拟 [3] 等。在监督学习框架中，数据集的正确输出是预先定义的，建立了一种从输入到输出的明确映射，这一过程涉及数据标记。而非监督学习则可以在不预先了解期望输出的情况下对数据进行处理，通过探索数据变量间的内在联系并聚类，实现对未知标签问题的预测。

在凝聚态物理学领域，相的分类和相变识别是重要研究课题 [4] ，随着处理系统的复杂度增加和状态量的膨胀，发现与分类相和相变的任务变得日益艰巨。伊辛模型，作为首个成功预测相变的模型，在长期的研究实践中已被誉为理论物理中最重要的模型之一 [5] 。近年来，蒙特卡罗方法联合机器学习技术 [4] [6] [7] [8] [9] ，共同被应用于相与相变的研究与发现之中。蒙特卡罗方法在此过程中的作用是生成机器学习所需的数据集，通过数值模拟计算热力学性质，从而数值地预测系统的平均行为。此方法的核心思想在于设计一种算法，以生成系统的一系列构型，使得经过一段时间后，每个构型均以合适的概率出现，从而准确描述系统的平衡状态 [10] 。

在本文中，我们将主成分分析(Principal Component Analysis, PCA)方法应用于铁磁性六方伊辛晶格，在没有任何关于自旋构型的微观理论或序参量信息的情况下，识别晶格中自旋结构的相、相变及其物理性质。我们发现PCA能够成功识别这六方伊辛晶格中的相变，并很好地估计相变临界温度T_c。

2. 模型

我们采用具有铁磁相互作用(J > 0)的六方伊辛晶格 [8] [11] 。如图1所示，在该系统的构型中，每个自旋都有三个与之相互作用的近邻。该系统的哈密顿方程如下：

$H=-J{\displaystyle {\sum }_{\langle i,j\rangle }{S}_i{S}_j}$ (1)

其中 $S_i=\pm \text{1}$ ， $\langle \rangle$ 表示最近邻，最近邻的相互作用J = 1。

当温度T降到临界值以下时，六方伊辛晶格会发生相变，自旋进入有序状态 [12] ：

$T_c=2J/K_B\text{ln}\left(2+\sqrt{3}\right)=1.519\left(J/K_B\right)$ (2)

Figure 1. Schematics for the three nearest neighbors (Blue) of one spin (Green) in the hexagonal Ising lattice

图1. 六方伊辛晶格中一个自旋(绿)的三个最近邻(蓝)示意图

3. 方法

我们在温度区间T/J = 3.0至0.3，每隔0.1取一个温度，在此温度下对六方伊辛晶格进行蒙特卡罗模拟，生成了一系列自旋构型。我们在每个温度下都生成300个自旋构型。这些构型构成了我们输入到非监督学习算法中的数据集。我们选用PCA作为非监督机器学习方法，用于探测六方伊辛晶格不同自旋构型相和相变。PCA作为一种有效的数据降维工具，能够在尽可能少损失信息的前提下，将高维数据简化到较低的维度，为我们揭示复杂系统中的相变提供了一种新的视角 [13] 。

我们将蒙特卡洛模拟获取的构型数据存为矩阵S，矩阵S的尺寸为M × N，其中M = 8400 = 28 × 300，N = L²，L是晶格的长宽尺寸。矩阵的每一行都是一个自旋构型。得到矩阵S后，下一步就是进行PCA分析。我们将S进行处理，算出每列的平均值，然后将该列元素减去该值，得到矩阵X。PCA通过对原始数据应用变换向量来找到主成分。

$Y=XW$ (3)

PCA的主要目的是找到一个或几个方向，在这些方向上，您可以在损失少量信息的情况下区分所有数据集。这意味着要寻找数据分布的最大方差。PCA正交变换是基于向量 $W=\left(w_1;w_2;\cdots ;w_N\right)$ ，我们的目标是确定矩阵X^TX最大的几个特征值相对应的特征向量。

$X^{\text{T}}X{w}_n={\lambda }_n{w}_n$ (4)

其中，w₁是差异最大的向量，表示特征值最大。主成分的计算公式为：

$Y_n=X{w}_n$ (5)

4. 结果和讨论

从图2(a)中我们可以发现，无论在哪个晶格尺寸下曲线从第一主成分到第二主成分之间都会发生骤降，之后相对平稳，显示出了任何晶格尺寸下第一个主成分都明显突出，这主要来自于低温下结构的极化特性与PCA方法的可靠性。图2(b)显示了与该主分量相匹配的稳定权重向量。观察 $w_1\simeq {\left(1/L,\cdots ,1/L\right)}^{\text{T}}$ ，利用公式(5)，并从X的某一行中选取一个特定磁构型，我们可以得到：

$Y_1=\frac{1}{L}\left[s_1,s_2,s_3,\cdots \right]\left[\begin{array}{c}1\\ 1\\ 1\\ ⋮\end{array}\right]=\frac{1}{L}{\displaystyle {\sum }_{i=1}^N{s}_i}$ (6)

这意味着第一个主成分确定了序参量，该序参量与系统的磁化强度相对应。

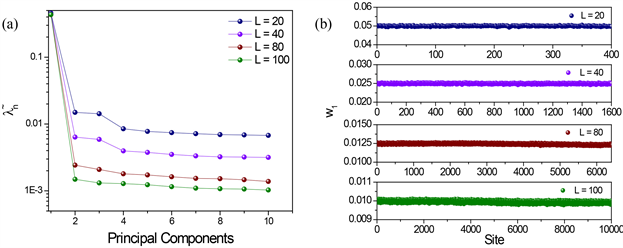
Figure 2. (a) Eigenvalues of different principal components by PCA; (b) Weights of the first principal components of hexagonal lattices with different sizes

图2. (a) 主成分分析获得的不同主方向的特征值；(b)不同尺寸六角晶格第一主成分权重

在图3中，我们可以看到由六方晶格自旋构型在前两个主成分构成的二维平面上的投影。从图中我们可以发现有三个不同的集群。靠近原点的点代表高于临界温度T_c的自旋构型，另外两个独立的区域代表低于临界温度的自旋构型。这一结果表明，PCA可以检测到体系中的相变。

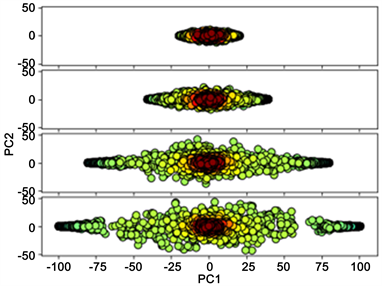
Figure 3. Projection of the spin configurations of the hexagonal lattices onto the plane of the first two principal components

图3. 六方晶格自旋构型在前两个主成分平面上的投影

图4(a)展示归一化第一主成分 $\langle \left|y_{\text{1}}\right|\rangle /L$ 与温度的关系。y₁/L代表晶格磁化强度m，

$m=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{s}_i}=\frac{y_1}{L}$ (7)

随着系统变大，我们可以更清楚地发现相变发生的值越来越接近着红色虚线所示的理论值。图4(b)展示归一化的第二主成分 $\langle \left|y_{\text{2}}\right|\rangle /L$ 随温度变化的关系，y₂/L代表晶格磁化率χ，磁化率的峰值很好地确定了相变临界温度。

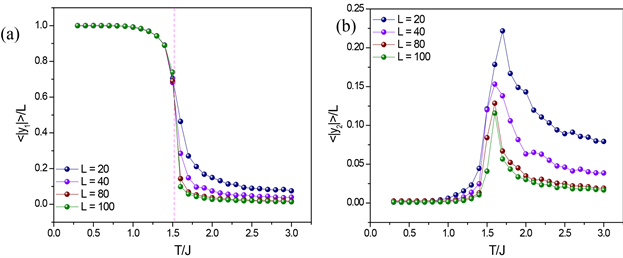
Figure 4. The normalized (a) first principal component and (b) second principal component versus the temperature

图4. 归一化(a)第一主成分和(b)第二主成分与温度的关系曲线

5. 结论

我们使用主成分分析方法(PCA)识别六方晶格的伊辛模型的相和相变，研究表明，PCA可以检测相变并确定相变临界温度。此外，第一和第二主成分还反映了模型的磁化强度和磁化率，表明机器学习可用于识别物理模型系统的特征。