1. 引言
中石化西北油田地处祖国的大西北,油田分布范围广,外部介质及气候环境因素复杂,油田钻井深度不断攀升。其中以顺北油气田为例,顺北油气田井下高温、高压、多种固液气介质共存,腐蚀环境极为复杂,在这些多因素联合作用下,容易引发采油油管管柱严重腐蚀问题,其中高含量的H2S会给井下管柱带来巨大的应力腐蚀开裂风险。此外,内外部的CO2气体侵蚀到管柱的内壁,与管柱所处的环境介质作用产生酸性介质,进一步对金属油管造成侵蚀 [1] [2] [3] 。目前使用的金属油管力学性能不足,耐腐蚀性能差,而常规聚合物油管耐压等级低、耐温性能差,不能满足井下工况越来越苛刻的需求。
目前,解决非金属管的耐高温性能低和抗压能力差的问题已变得十分迫切。鉴于高温聚合物因其高温稳定性好、密度低、化学惰性强,且碳纤维、SiC纤维具有比强度高,比刚度与比模量大等良好的机械性能,将二者进行复合将是一个非常好的材料设计思路 [4] [5] [6] 。利用短纤维增强层内、长纤维增强层间的方式,制备了适用于顺北井下高温环境的非金属轻量化复合油管,这将具有一定的理论意义与工程价值。通过具有一定长度及取向的短纤维与一定编排结构的长纤维协同增强,来实现聚合物基复合材料油管的设计、结构优化与制备。并完成相应的工程化应用研究,解决现场面临的问题。从而有望满足顺北油田非金属油管的高强度、抗腐蚀、轻量化、降成本的现场需求。
为了提高非金属聚合物基复合材料油管的力学性能,一种有效的方法是采用多尺度的协同增强复合材料。这种复合材料通过在不同的尺度上引入不同的增强相,实现了基体和增强相之间的协同作用,从而提高了复合材料的整体性能。例如,通过挤塑成型并作为非金属聚合物基复合材料油管基材,再通过缠绕成型铺设一定角度取向及层数的长纤维制备非金属油管,就是一种多尺度协同增强复合材料的典型代表。这种复合材料不仅利用了长纤维的高强度和高模量,还利用了短纤维的高韧性和高延展性,实现了油管的高强度和高韧性的平衡。
通常考虑到实际工艺,将短纤维(通常为碳纤维或碳化硅纤维)与树脂(环氧树脂或双马树脂)基体混合后,通过挤塑成型并作为非金属聚合物基复合材料油管基材,再通过缠绕成型铺设一定角度取向及层数的长纤维制备非金属油管 [7] [8] 。基于抗内压强度,径向压溃强度及轴向拉伸强度的各项指标来实现非金属油管的优化设计 [9] [10] [11] 。同时基于非金属油管在210℃条件下的本构关系实现在高温下的非金属油管的结构设计,使其在承受一定扭转载荷作用时,强度及变形量均满足设计要求。
对于长度较低的非金属聚合物基复合材料油管,其力学性能可以通过实验手段予以检测 [12] [13] ,然而随着新疆中石化塔里木油田采油井深的不断攀升,迫切需要更长的聚合物基复合材料油管,因此超长的非金属油管的力学性能的检测成为面临的现实难题,有限元数值模拟是一种有效的手段,能够基于虚拟的仿真情景实现相关的计算。
针对10,000米超长非金属聚合物基复合材料油管,采用一维线性单元技术Pipe288,开展油管力学性能的优化计算与预测。首先根据多尺度协同增强复合材料油管的结构特点,建立了一维线性单元的力学模型。然后,利用ANSYS软件,基于Pipe288单元,建立了10,000米超长非金属聚合物基复合材料油管的有限元模型,分析了油管在不同的工况下的应力、应变和变形的分布规律,探讨了油管的力学性能和可靠性的影响因素,优化了油管的设计参数和工作参数,从而验证了本文的模型和方法的准确性和有效性。
本文的研究为10,000米超长非金属聚合物基复合材料油管力学性能的分析和预测提供了一种简便可行的方法,具有较大的创新性和应用价值。通过具有一定长度及取向的短纤维与一定编排结构的长纤维协同增强,来实现聚合物基复合材料油管的设计、结构优化与制备。并完成相应的工程化应用研究,解决现场面临的问题。从而有望满足顺北油田对非金属油管的高强度、抗腐蚀、轻量化、降成本的现场需求。
2. 模拟理论与方法
要计算纤维增强聚合物基复合材料油管的力学性能,必须明确油管本身的本构关系,而要得到油管本身的本构关系,必须从最基本的“基元”开始,即通过短纤维增强的聚合物基复合材料得到单层复合结构的本构关系,然后通过长纤维编织得到多层复合材料结构的本构关系,进而得到聚合物基复合材料油管的本构关系,在求解“基元”的力学本构时,采用拉伸强度进行计算时,是常用的计算力学性能的手段。
2.1. 短纤维增强聚合物复合体系
对于短纤维增强聚合物复合体系,其拉伸强度与纤维的临界长度
息息相关。若界面粘结强度很高,则
可由下式表述 [14] [15] :
(1)
式中
为纤维直径,
为纤维的拉伸强度,
为纤维与基体的剪切强度。如果纤维长度大于其临界长度且完全平行于取向方向,则复合体系的拉伸强度可用式(2)计算:
(2)
式中
是纤维的体积分数,
为基体的拉伸强度。如果纤维轴向并不完全平行于取向方向,则复合体系的拉伸强度可用式(3)计算:
(3)
式中
为纤维取向因子,反应了纤维的取向程度和方向。短纤维增强聚合物复合体系的横向拉伸强度可由下式估算:
(4)
式中,
为复合材料界面粘结强度。类似地,基于短纤维在树脂基体中均匀分散及取向等假设,引人界面强度因子的概念,可导出如下的增强聚合物复合体系相对拉伸强度公式:
(5)
式中,
称为界面强度因子,
和
分别代表纤维的长度和直径。
2.2. 长纤维增强聚合物复合体系
对于长纤维增强聚合物复合材料体系,其拉伸强度在相当程度上取决于纤维的取向及取向度。若纤维轴向完全平行于取向方向,则聚合物复合材料体系的纵向拉伸强度可用混合法则进行估算 [16] [17] [18] :
(6)
式中
为纤维拉伸强度。如果纤维轴向并非完全平行于取向方向,则可用下式进行估算:
(7)
式中,K为纤维的取向度。当载荷作用为任一方向时,复合材料在该方向的拉伸强度(
)可表示为:
(8)
式中
为载荷作用方向与纤维取向之间的夹角。
,
及
分别为复合材料纵向拉伸强度,横向拉伸强度及切向强度。显然,
随着角度
的增加而急剧下降。一般来说,复合体系的横向拉伸强度和剪切强度主要取决于树脂基体的强度 [19] [20] [21] ,此时,
可由下式表示:
(9)
由于深井钻管无法通过试验进行工程预演,因此只能通过计算机仿真技术建立符合实际工况的力学模型进行求解。10,000米深井管道在各类工况作用下每隔1000米处宏观应力及应变分析,仅考虑管道内压、外压、拉力、扭矩等荷载,不考虑管道与土壤等摩擦作用力,考虑材料非线性因素。
2.3. 超长油管力学性能计算的有限元模型
本文根据文献调研以及工程实际工况要求,设计如图1所示的内外双层结构油管。其中内层通过短纤维增强的复合材料结构,在生产制造上可通过挤塑成型制备,在内层成型基础上,外层采用常规长纤维增强复合材料结构直接缠绕在内层结构上,从而形成短纤维和长纤维多尺度协同增强的复合材料油管。尽管纤维的编排具有一定的方向性,但由于实际材料存在不规则随机分布的孔隙,因此各个方向对外力学性能差异不大,因此为简化计算,抓住本文研究的关键问题,将材料本构视为各向同性。

Figure 1. The concept diagram of the internal and external double-layer structure design of the tubing string
图1. 油管管柱内外双层结构设计概念图
在超长油管的力学性能的有限元计算中,本文采用碳纤维增强双马来酰亚胺树脂基复合材料,给定的管道几何及材料参数见表1。

Table 1. Geometry and material parameters
表1. 几何及材料参数
所设定油管的长度从0米(管口的端部),1000米、2000米、3000米、4000米、5000米、6000米、7000米、8000米、9000米、10,000米。有限元模拟计算中所施加的载荷及工况组合见表2。

Table 2. Load and working condition combination
表2. 载荷及工况组合
其中:x为离海平面的距离(米),外压等于静水压强。
。
如果采用Solid70等三维单元,建立长达几千米甚至万米的油管的模型进行计算,将导致网格数量巨大,计算效率极低甚至导致机器死机无法进行计算,即使计算出来,要提取关键部位的应力及应变分布也将是一个巨大的挑战。因此,本文采用Pipe288单元进行管道应力分析,从而取代三维单元的计算,不仅提高了计算效率,而且计算的结果同样精确可靠,即是将一个三维复杂的问题转化为一维线性单元予以计算,并且还能够求解非线性问题。Pipe288单元是一维单元,如图2所示,是ANSYS单元库中专门用于分析管道问题的单元,可以真实的模拟各类内压、外压、拉力和扭矩等荷载。pipe288单元的基本特点如下:Pipe288单元适合模拟细长到中粗的各类管道,依据铁木辛柯理论,考虑一阶剪切效应。每个Pipe288单元含有2个节点,每个节点含有6个自由度(平动自由度x、y、z,转动自由度Rotx、Roty、Rotz),单元可适合做线性、大转动和大应变的非线性分析。虽然节点数只有两个,但是该单元可以定义截面形状,并通过截面栅格及积分点技术,精确捕捉各类荷载(包括内压、外压等)在截面内的应力分布。与Pipe288单元相比,其他类似的结构单元,如Beam188单元、Bar189单元、Link180单元等,都有一定的局限性和不足。例如,Beam188单元只能考虑管道的弯曲和扭转,不能考虑管道的拉伸和压缩;Bar189单元只能考虑管道的拉伸和压缩,不能考虑管道的弯曲和扭转;Link180单元只能考虑管道的轴向力,不能考虑管道的弯矩和扭矩。因此,Pipe288单元是一种更为通用和灵活的结构单元,更适合本文的研究目的和内容。

Figure 2. (a) Schematic illustration of Pipe288 element; (b) Unit cross-section grid
图2. (a) Pipe288单元示意图;(b) 单元截面栅格示意图
有限元模拟中使用的材料本构如表3所示。

Table 3. Material constitutive used in the process of finite element simulation
表3. 有限元模拟中使用的材料本构
通过SpaceClaim及Workbench相结合建立线体并赋予截面属性,得到管道几何模型。如图3所示。

Figure 3. (a) Geometric model of part of the pipeline; (b) Cross-section; (c) Part of the elements
图3. (a) 部分管道几何模型;(b) 截面;(c) 部分单元示意图
通过ANSYS网格划分技术,取1米管长为一个pipe单元,单元长度/直径 = 14,属于合理管单元长径比范围,故共划10,000个pipe单元。1,1000~1001,2000~2001,3000~3001,4000~4001,5000~5001,6000~6001,7000~7001,8000~8001,9000~9001,10,000以上各单元组合可作为0米、1000米、2000米、3000米、4000米、5000米、6000米、7000米、8000米、9000米和10,000米深度下管道部分。总节点数为20,001;总单元数为10,000。
边界条件与载荷设置如下:将管道在井深远端处固定,地面端施加预拉力、扭矩。管道截面积
,因此预拉力
,扭矩 = 3000 Nm,
内压 = 150 MPa,外压通过函数形式加载:外压 = 9800x (Pa),在分析设置中,打开大变形开关。设置两个载荷步,第一个载荷步添加内压、外压、拉力,内设300个载荷子步以精确模拟应力应变关系。第二个载荷步在第一步基础上添加扭矩,设初始子步 = 500,最大子步 = 1,最小子步 = 800,以解决几何非线性及材料非线性综合效应。
3. 结果与讨论
有限元计算得到的各工况应力、应变结果如表4所示。
在油管长度对应0 m (油管端口处),5000 m,10,000 m的工况一、工况二应力应变云图如图4和图5所示。通过有限元模拟,可计算其在复合载荷作用下的非金属油管的应力云图,不难看出,其最大等效拉应力、最大拉应变、最大主应力及最大剪应力均分布在油管的内壁。
且进一步不难看出,随着井深增加,对应的油管长度增加,端口处的最大等效拉应力、最大拉应变、最大主应力及最大剪应力呈现递减趋势。
对比工况一,在相同长度的油管条件下,工况二所对应的最大等效拉应力、最大拉应变、最大主应力及最大剪应力均高于工况一。这是由于工况二在工况一的基础上添加了扭矩。

Table 4. Stress-strain results for each working condition
表4. 各工况应力应变结果
 (a)~(d)为0 m (油管端口)处;(a′)~(d′)为5000 m处;(a″)~(d″)为10,000 m (油管端口)处。
(a)~(d)为0 m (油管端口)处;(a′)~(d′)为5000 m处;(a″)~(d″)为10,000 m (油管端口)处。
Figure 4. Contour plot of equivalent (von-Mises) stress, maximum principal strain contour, maximum principal stress contour and maximum shear stress contour for working condition 1
图4. 工况一等效(von-Mises)应力云图,最大主应变云图,最大主应力云图及最大剪应力云图
工况一条件下应力,应变随着井深的变化曲线及不同油管长度最大主应力–最大主应变关系曲线最大主应力–最大主应变关系曲线如图6所示。由图6(a)不难看出,随着井深的增加,最大主应力及最大主应变均呈现递减的趋势。由图6(b)不难看出,在0 m条件下,即油管的最左端口处,最大主应力与最大主应变呈现双线性特征,开始阶段,随着最大主应变增加,最大主应力线性增加,当最大主应变超过一定
 (a)~(d)为0 m (油管端口)处;(a′)~(d′)为5000 m处;(a″)~(d″)为10,000 m (油管端口)处。
(a)~(d)为0 m (油管端口)处;(a′)~(d′)为5000 m处;(a″)~(d″)为10,000 m (油管端口)处。
Figure 5. Contour plot of equivalent (von-Mises) stress, maximum principal strain contour, maximum principal stress contour and maximum shear stress contour for working condition 2
图5. 工况二等效(von-Mises)应力云图,最大主应变云图,最大主应力云图及最大剪应力云图

Figure 6. (a) Variation curve of stress and strain as the function of the well depth under working condition 1; (b) The maximum principal stress vs. maximum principal strain (0 m); (c) Maximum principal stress-maximum principal strain (5000 m); (d) Maximum principal stress vs. maximum principal strain (10,000 m)
图6. (a) 工况一条件下应力,应变随着井深的变化曲线;(b) 0米最大主应力–最大主应变关系曲线;(c) 5000米最大主应力–最大主应变关系曲线;(d) 10,000米最大主应力–最大主应变关系曲线
值时,出现拐点,此时随着最大主应变增加,最大主应力进一步线性增加,但增加的趋势减小,其对应的斜率降低。由图6(c)不难看出,在5000米长度的油管条件下,应力和应变呈现先减小后增大趋势,在增加的阶段呈现三线性特征,对应的线性斜率逐渐递减,表明其最大主应力随着最大主应变的增加,其增加的趋势变缓。由图6(d)不难看出,在10,000米长度的油管条件下,应力和应变呈现先减小后增大趋势,在增加的阶段呈现单线性特征,其最大主应力随着最大主应变一直保持相同的速率在递增。
工况二条件下应力,应变随着井深的变化曲线及不同油管长度最大主应力–最大主应变关系曲线最大主应力–最大主应变关系曲线如图7所示。与工况一相比,图7(c)在增加的阶段呈现四线性特征,在前3个线性阶段,对应的线性斜率逐渐递减,表明其最大主应力随着最大主应变的增加,其增加的趋势变缓。但到了第4线性阶段,其斜率又进一步提高,表明,随着最大主应变增加,其最大主应力增加的趋势进一步加重,图7(d)在增加的阶段呈现双线性特征,开始阶段,其最大主应力随着最大主应变一直保持相同的速率在递增。在第二个线性阶段,其斜率省略有减小,表明,随着最大主应变增加,最大主应力增加的趋势变缓。
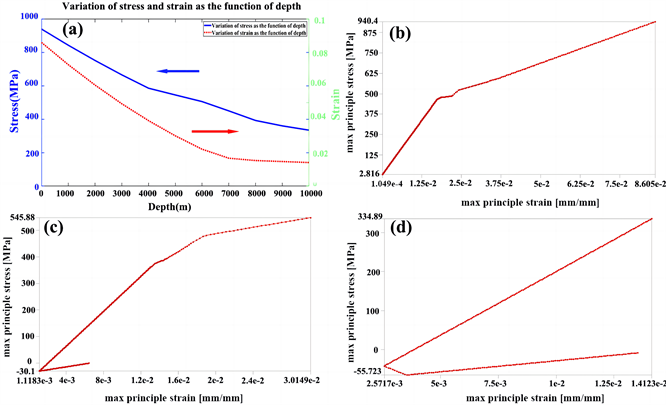
Figure 7. (a) Variation curve of stress and strain as the function of the well depth under working condition 2; (b) The maximum principal stress vs. maximum principal strain (0 m); (c) Maximum principal stress-maximum principal strain (5000 m); (d) Maximum principal stress vs. maximum principal strain (10,000 m)
图7. (a) 工况二条件下应力,应变随着井深的变化曲线;(b) 最大主应力–最大主应变关系曲线(0 m);(c) 5000米最大主应力–最大主应变关系曲线;(d) 10,000米最大主应力–最大主应变关系曲线
各工况应力、应变云图可以得到如下结论:管壁截面各应力应变等值线分布呈环形,这与荷载对中心轴呈中心对称分布相符(即对整体管道不出现弯矩)。从各工况最大主应力–最大主应变关系曲线可以得到如下结论:随着深度的加深,应力和应变愈发呈现先减小后增大趋势。从各工况应力、应变随深度变化曲线可以得到如下结论:随着深度的增加,各应力应变呈现单调递减趋势。最危险截面位于靠近地面附近,原因是此处内外压压差最大,产生的应力最大。
当然,从得到的应力应变数据可知,不论采用第四强度理论(von-Mises准则),第一强度理论(最大主应力准则),第三强度理论(最大剪应力理论)计算,所得到的应力均大于材料屈服强度及抗拉强度,即在当前工况下,材料的强度不足以支撑,从而会导致超长非金属聚合物基复合材料油管发生损伤失效。因此,初步判断,管道强度不足。后续可通过对复合材料进行结构设计,增强管道本体强度解决这一问题。
4. 结论
本文针对超长非金属聚合物基复合材料油管,采用一维线性单元技术取代计算量庞大无法计算的三维单元技术,实现了10,000米超长非金属聚合物基复合材料油管力学性能的计算,获得如下结论:
(1) 通过计算各工况应力、应变云图表明管壁截面各应力应变等值线分布呈环形,这与荷载对中心轴呈中心对称分布相符(即对整体管道不出现弯矩);
(2) 随着井深深度的加深,应力和应变愈发呈现先减小后增大趋势。随着深度的增加,各应力应变呈现单调递减趋势。最危险截面位于靠近地面附近,原因是此处内外压压差最大,产生的应力最大;
(3) 计算所得到的应力大于材料屈服强度及抗拉强度。因此后续可通过对材料结构进行设计,增强管道本体强度来进一步增强聚合物基复合材料油管的力学性能。
NOTES
*通讯作者。