1. 引言
支持向量机(Support Vector Machines, SVMs)是二十世纪九十年代中期在统计学习理论基础上发展起来的一种新型机器学习方法[1] 。传统统计学是样本数目趋于无穷大时的渐近理论,但在实际问题中,样本数往往是有限的,因此一些理论上很优秀的学习方法在实际中的表现却可能不尽人意[2] 。统计学习理论是研究小样本统计估计和预测的理论,Vapnik等人从二十世纪六、七十年代开始致力于此方面研究,统计学习理论的主要内容包括以下四个方面[3] :一是经验风险最小化准则(Empirieal Risk Minimization, ERM)下统计学习一致性条件;二是统计学习方法推广性的界;三是在推广性的界的基础上建立的结构风险最小化原则;四是实现这些准则的支持向量机方法。
支持向量机采用结构风险最小化准则(Structural Risk Minimization, SRM)训练学习机器,其主要优点有[4] :将学习问题归结为一个凸二次规划问题,从理论上说,得到的将是全局最优解,解决了在神经网络方法中无法避免的局部极值问题;通过非线性变换将数据映射到高维特征空间,使数据在高维空间中可以用线性判别函数分类;巧妙地解决了维数问题,算法复杂度与样本维数无关;具有简洁的数学形式和直观的几何解释,人为设定的参数少,便于理解和使用。支持向量机建立在严格的理论基础之上,较好地解决了非线性、高维数、局部极小点等问题,成为继神经网络研究之后机器学习领域新的研究热点。
针对SVM这种算法选取参数不完善的地方,选取参数的算法需具备较强的普遍性,收敛速度快,计算量小和全局搜索能力强的要求,本文利用张英男[5] 等人提出的活跃目标点粒子群算法对SVM参数进行选取。通过仿真实验可以看出改进的粒子群算法能够选出较为有效的算法。
2. SVM基本原理
支持向量机最初是用来处理两类数据的分类问题,它试图寻找一个能够分离两类点的一个超平面,并让这些点和超平面的距离最大化。如图1所示,三角形和圆圈分别表示两类训练样本,把它们投射到高维特征空间,寻找一个超平面H,能够把这两类正确的分离开,并使两类距离超平面最近的点与超平面的距离最大,即H1和H2与H的距离最大化,H1与H2之间的距离即为分类间隔。H所表示的就是最优超平面。
SVM的主要思想可以概括为两点:1) 它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能;2) 它基于结构风险最小化的原则,构造了一个目标函数,使得两类模式尽量正确的区分开。设训练样本为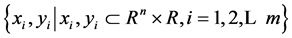 ,将这个输入向量映射到高维特征空间,并在该特征空间构造最优分类面,将SVM回归表示为:
,将这个输入向量映射到高维特征空间,并在该特征空间构造最优分类面,将SVM回归表示为:
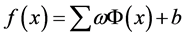 (1)
(1)
其中: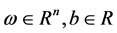 。
。
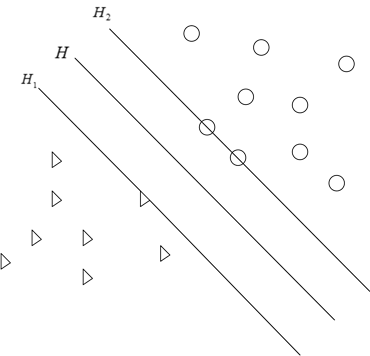
Figure 1. The optimal hyperplane
图1. 最优超平面示意图
将其转化为解凸二次优化问题,即:
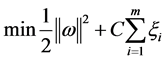 (2)
(2)
满足约束条件:
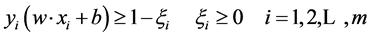 (3)
(3)
为解决最优化问题,其对偶问题为:
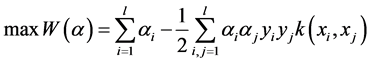 (4)
(4)
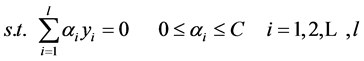 (5)
(5)
决策函数为:
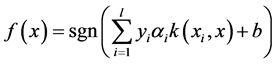 (6)
(6)
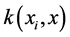 为满足Mercer条件的核函数。
为满足Mercer条件的核函数。
本文采用RBF核函数,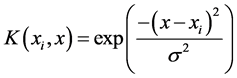 ,
,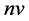 为支持向量个数。
为支持向量个数。
3. 活跃目标点粒子群算法
Kennedy和Eberhart于1995年基于生物界中鸟群和鱼群等生物群体的捕食行为,提出的粒子群优化(PSO)算法。在自然界中,鸟搜索食物是通过群体合作实现的,即搜索离食物最近的鸟的周围的区域。我们称这些鸟为“粒子”,粒子具有各自的速度和位置,算法中还有一个适应度函数,在每一次迭代中寻找这一代的最优解和历史最优解以获得下一次迭代所需要的速度,从而来对“粒子”的状态进行改变,直到达到全局最优解或者满足终止条件。
3.1. 标准POS算法
Kelmedy和Eberhart的标准全局版PSO算法可概述如下[6] :假设在一个d维的目标搜索空间中,由M个粒子组成一个种群,其中第i个粒子位置表示为一个d维的向量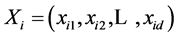 ,速度表示为d维向量
,速度表示为d维向量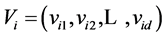 。
。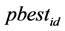 为第i个粒子的历史最优位置,
为第i个粒子的历史最优位置,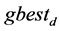 为这一代粒子的全局最优位置,则第i个粒子速度和位置的更新公式为:
为这一代粒子的全局最优位置,则第i个粒子速度和位置的更新公式为:
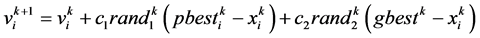 (7)
(7)
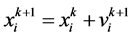 (8)
(8)
其中,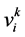 是粒子i在第k次迭代中的速度向量,
是粒子i在第k次迭代中的速度向量,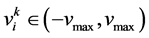 ,
,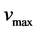 用于限制粒子速度,使之在一定的范围内飞行,不会应为速度过小导致陷入局部最优或者速度过大飞离最优解区域;c1,c2是学习因子,c1为个体历史最优粒子对第i个粒子飞行速度的影响,c2为全局最优粒子对第i个粒子飞行速度的影响,rand1,rand2是[0,1]之间的随机数。
用于限制粒子速度,使之在一定的范围内飞行,不会应为速度过小导致陷入局部最优或者速度过大飞离最优解区域;c1,c2是学习因子,c1为个体历史最优粒子对第i个粒子飞行速度的影响,c2为全局最优粒子对第i个粒子飞行速度的影响,rand1,rand2是[0,1]之间的随机数。
SVM参数取值对于最终能否进行正确的分类有着重要的关系。其参数包括惩罚因子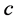 和核参数
和核参数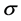 。因此我选用了改进的PSO算法,即APSO,来对
。因此我选用了改进的PSO算法,即APSO,来对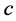 和
和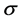 进行选取。
进行选取。
3.2. APSO算法
为避免标准PSO早熟收敛陷入局部最优解,活跃目标点粒子群算法(APSO)在标准PSO的速度更新中引入了第三个目标点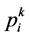 ,区别于种群当代最优和粒子历史最优的位置,使粒子能够跳出局部最优解,所引入的第三个点
,区别于种群当代最优和粒子历史最优的位置,使粒子能够跳出局部最优解,所引入的第三个点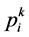 即为活跃目标点[7] 。该点是利用当前粒子i的邻域中按一定规则随机搜索一点
即为活跃目标点[7] 。该点是利用当前粒子i的邻域中按一定规则随机搜索一点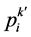 ,与pbest和gbest构成复合型,进而求得一个该点
,与pbest和gbest构成复合型,进而求得一个该点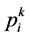 。APSO可以较好地保持种群多样性,跳出局部最优能力较强,并且进入搜索后期也可以保持较快的收敛速度,但缺点是每次迭代增加了一次随机点的计算。
。APSO可以较好地保持种群多样性,跳出局部最优能力较强,并且进入搜索后期也可以保持较快的收敛速度,但缺点是每次迭代增加了一次随机点的计算。
APSO的速度更新公式为:
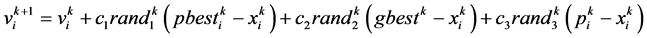 (9)
(9)
其中,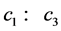 为学习因子;
为学习因子;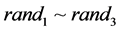 为[0,1]之间的随机数;
为[0,1]之间的随机数;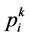 为活跃目标点。下面给出求解活跃目标点
为活跃目标点。下面给出求解活跃目标点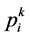 的步骤:
的步骤:
1) 在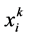 邻域范围内搜索一点作为试用活跃目标点
邻域范围内搜索一点作为试用活跃目标点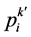 :
:
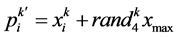 (10)
(10)
其中,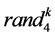 是
是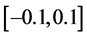 之间的随机数;
之间的随机数;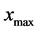 为最大可行域范围。
为最大可行域范围。
2) 在粒子历史最优点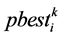 ,种群历史最优点
,种群历史最优点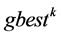 和试用目标点
和试用目标点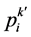 三点中找出最坏点
三点中找出最坏点
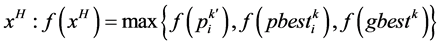 (11)
(11)
设最坏点为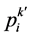 ,进行最坏点映射:
,进行最坏点映射:
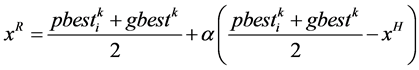 (12)
(12)
其中,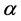 为映射系数,
为映射系数,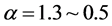 ,呈递减趋势。
,呈递减趋势。
最后,将该映射点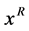 作为活跃目标点
作为活跃目标点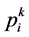 的位置。即
的位置。即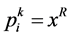 。
。
4. 仿真实验——SVM参数选取
由文献[8] 给出的某柴油机燃油喷射系统的柱塞在正常和磨损状态下经过多次采用并经AR时序建模而得到的压力波形特征参数,表1为柱塞不同磨损状况时的9个标准样本。
首先随机生成粒子的初始位置和初始速度,并以SVM计算的准确率为其适应度,然后寻找其个体历

Table 1. Parameters of pressure wave of plungers that have abrasion and not have abrasion
表1. 柱塞磨损与不磨损时的压力波特征参数
史最优值和群体最优值,之后进行迭代,更新个体历史最优值和群体最优值,直到满足终止条件。最优位置即为所需要的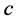 ,
,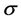 ,经由SVM计算出其准确率。
,经由SVM计算出其准确率。
在采用APSO来优化SVM时,其分类的准确度要远远高于GA和PSO优化SVM后分类的准确度,表2为不同寻优方式下SVM分类的准确率和对应的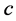 和
和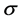 。
。
结果表明,基于APSO的SVM参数选取在分类准确率上要优于其他两种优化方法,在非线性可分情况下有较高的准确性。
5. 总结
SVM被广泛的用来进行非线性分类,模式识别与故障诊断。有神经网络不具有的优越性。而对于SVM需要设定一定的参数才能进行准确的分类,其参数是根据不同的分类情况进行选定的。本文利用APSO来优化SVM参数的选取,通过仿真实验表明,经过APSO优化的SVM拥有更好的分类效果。该方法的优点是分类准确率高,缺点是计算量高,可以通过RS理论对条件进行化简,使得计算量减少,这是以后下一步准备做的。