1. 引言
在多径衰落环境中，多输入多输出(MIMO)技术使用多个发送天线和接收天线可以显著提高系统的容量和改善无线传输链路的质量而不增加系统的带宽[1] 。MIMO技术已经成为无线通信领域的研究热点，尤其在信道相关的测量、建模和信道编码方面有了广泛的学术成果[2] -[4] ，受到越来越多的关注。空时编码(STBC)就是利用MIMO技术有效地实现了空间分集，尤其正交空时分组码(OSTBC)以较低的译码复杂度获得了完全的分集增益。然而，典型的MIMO系统中发射机和接收机同时使用所有的天线发射和接收，这就要求使用与天线一样多的射频链路，大大增加了系统的硬件成本，而且空时编码、检测译码等信号处理的复杂度也会大幅度提高。发射天线选择(TAS)技术由于用相对较少的收发射频链路支持较多的天线，大幅削减了硬件成本，并且降低了信号处理的复杂度，因此引起人们极大的关注。文献[5] 利用TAS和STBC的优点，提出了TAS/STBC方案，选择两根发射天线的系统称为TAS/Alamouti。文献[6] -[8] 利用矩生成函数(MGF)的方法，研究了相互独立的瑞利衰落信道上采用TAS/Alamouti方案和相干检测的BFSK、M进制相移键控(MPSK)和方形M进制正交幅度调制(MQAM)的平均符号误码率(ASEP)的精确闭合表达式及其性能上限。文献[9] 进一步分析了在相互独立的Nakagami-m信道下发射端选择两根和三根天线时TAS/STBC系统的ASEP性能。
但是上述文献的工作主要是研究独立信道下的TAS/STBC系统的ASEP性能。在实际的物理信道中，往往没有丰富的散射环境。同时，由于天线分布、天线间距、波达方向和角度扩展等因素的影响，衰落信道之间往往是相关的，信道的相关性会影响TAS/STBC系统的ASEP性能。本文正是针对这个问题，研究了TAS/STBC系统在相关Rayleigh信道下的性能。首先，我们采用了非常适合室内信道的Laplacian模型，得到了两个天线之间的相关系数，它是天线间隔，功率方位角谱(PAS)的标准差和平均到达角(AOA)三者的函数。然后我们从独立的Rayleigh信道开始，引入了相关矩阵，建立了相关Rayleigh信道模型；最后，我们利用建立的相关信道模型，利用文献[10] 中的方法，将TAS/STBC系统的相关矩阵信道等效成一个标量加性高斯白噪声(AWGN)信道，推导出了系统在接收端信噪比的表达式，并对不同条件下的ASEP性能做了数值仿真，验证了分析结果的正确性，为TAS/STBC系统设计提供有效的理论分析工具。
2. 系统模型
下面我们对TAS/STBC系统进行说明，图1是TAS/STBC系统的发射机框图，图2是TAS/STBC系统的接收机框图。
假设TAS/STBC系统有K根发射天线，M根接收天线。我们假设接收端可以获得理想信道状态信息(CSI)，发射端未知信道信息，接收端根据CSI从K个发射天线中选择使接收信噪比(SNR)最大的N根发射天线进行STBC编码，每次信道使用的总发射功率Es在选定的N个天线上平均分配。输入的信息序列经过调制后，生成S个符号，经STBC编码后在T个时隙内由选择出的N个天线发射出去。每对天线之间的无线信道是相互独立的，独立Rayleigh信道的矩阵H可以表示为
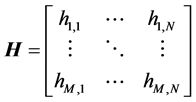(1)
其中元素hij表示发射天线j到接收天线i的复路径增益，服从Rayleigh分布。
接收端的信号可以表示为
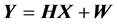(2)
其中Y是M × T维的接收信号矩阵，X是N × T维的发射信号矩阵，W是M × T维的复高斯白噪声矩阵，其方差是N0/2IM，IM是M × M维的单位矩阵，N0是功率谱密度。
在实际环境中，发射端和接收端的天线之间是相关的，用Rt表示发射端的相关矩阵，Rr表示接收端的相关矩阵。根据文献[11] ，相关Rayleigh信道的矩阵可以表示为：
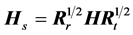(3)
为了计算Rt和Rr，需要先计算两根相邻天线间的空间相关系数。我们考虑一种通用的线性天线阵列，线性天线阵列使用全向天线。图3描述了这种线性天线阵列模型。
如图3所示，我们用a和b来代表两根相邻的天线，它们之间的间隔是d。对于到达a和b的接收信号，其平均到达角(AOA)为θ0，那么它们之间的距离差是dsin(θ0)，相应的延迟是ω0 = (d/c)sin(θ0)，c表示光速。我们分别用ha(θ)和hb(θ)代表二者的冲击响应，θ是接收信号的到达角。所以，a和b之间的空间相关系数可以表示为[12] ：
Figure 1. The transmitter block diagram of TAS/STBC system
图1. TAS/STBC系统的发射机框图
Figure 2. The receiver block diagram of TAS/STBC system
图2. TAS/STBC系统的接收机框图
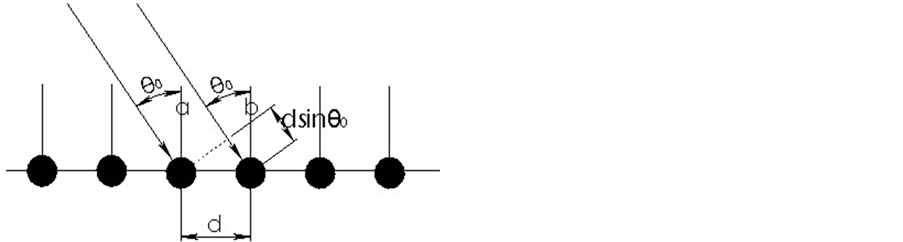
Figure 3. The linear antenna array model
图3. 线性天线阵列模型
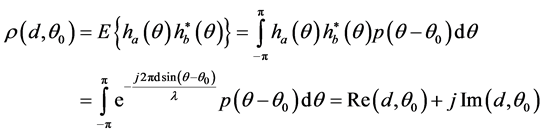(4)
在这里，E{}表示求均值，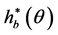
表示hb(θ)的共轭，p(θ)是功率方位角谱，λ是信号的波长。
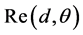和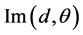
分别表示空间相关系数的实部和虚部。
我们使用一种Laplacian模型表示功率方位角谱。设定PAS的标准差为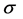
，定义Laplacian模型的功率方位角谱为[12] ：
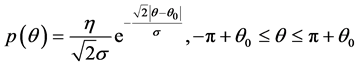(5)
使用下面的公式来求η
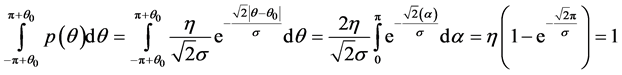(6)
因此η可以表示为
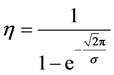(7)
我们已经知道Laplacian模型的功率方位角谱，只要把式(5)和式(7)带入式(4)，就可以求出空间相关系数，如下面所示：
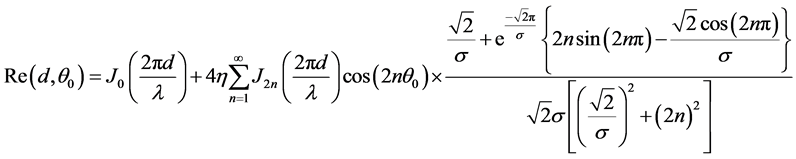(8)
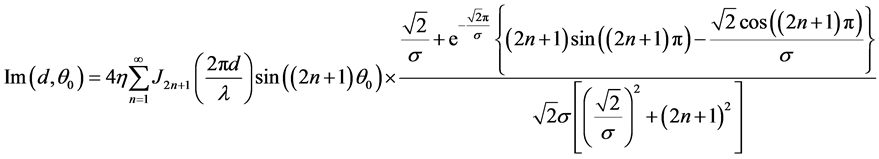(9)
其中Jm()表示第一类m阶贝塞尔函数。我们从式子(8)和(9)可以看出：天线间隔d，中心入射角θ0和功率方位角谱的标准差σ是影响空间相关系数的决定因素。
已知两根相邻天线间的空间相关系数，进而就可以求出发射端和接收端的相关矩阵，建立相关Rayleigh信道的模型。相关Rayleigh信道矩阵用Hs表示。我们利用等效的标量AWGN信道的方法，此时系统的接收信号可以表示为
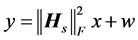(10)
考虑STBC的编码速率，用R表示，接收信号可以表示为
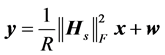(11)
y是经过STBC译码后的S × 1维的接收信号矩阵，x是S × 1维的发射信号矩阵，w是S × 1维的高斯白噪声矩阵，其每一维的期望是0，方差是1/R ×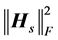
× N0/2。
因此接收端的比特信噪比可以用r0表示为
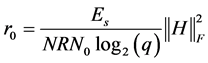(12)
我们用h0进行一下替换，即
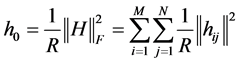(13)
则(11)，(12)式可以表示为
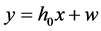(14)
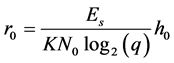(15)
发射天线选择的准则是使接收端的接收信噪比(SNR)最大，这样可以减小误码率。我们由(15)式可以得到，接收信噪比r0最大，则h0最大，所以当从K根发射天线中选出N根时，共有K!/(N!)/(K − N)!种选择，z表示其中的一种选择，那么最佳的发射天线选择可以表示
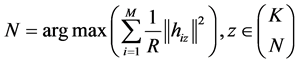(16)
3. 数值仿真
我们将此TAS/STBC系统简记为(K, M; N × M)。在这里，发射天线数目K取3根，接收天线数目M取2根，从K中选择N根发射天线，其中N取2根发射天线，记为(3, 2; 4)。下面分析信道的相关性对TAS/STBC系统性能的影响。
图4给出了TAS/STBC系统分别在独立Rayleigh信道和相关Rayleigh信道下，使用QPSK调制方式，ASEP性能随总发射信噪比变化的曲线。天线间隔d = λ，中心入射角θ0 = 20˚，功率方位角谱(PAS)的标准差σ = 5˚。由图4可知，TAS/STBC系统在独立Rayleigh信道下的ASEP性能要比相关Rayleigh信道下的ASEP性能好。当信噪比比较低时，二者的差距还是比较小，随着发射信噪比的增加，二者的差距是不断增大的。例如，当信噪比为2 dB时，TAS/STBC系统在独立Rayleigh信道下的误码率为4 × 10−3，在相关Rayleigh信道下的误码率为6 × 10−3；当信噪比为8 dB时，TAS/STBC系统在独立Rayleigh信道下的误码率为3 × 10−5，在相关Rayleigh信道下的误码率为2 × 10−3。
图5给出了TAS/STBC系统在不同天线间隔下，使用QPSK调制方式，ASEP性能随总发射信噪比变化的曲线。天线间隔d分别取λ、2λ、3λ。中心入射角θ0 = 20˚，功率方位角谱(PAS)的标准差σ = 5˚。由图5可知，当信噪比比较低时，三者的差距还是比较小，随着发射信噪比的增加，三者的差距是不断增大的。随着天线间隔d的不断增大，TAS/STBC系统在相关Rayleigh信道下的ASEP性能也是越来越好，例如，当信噪比为10 dB时，d = λ，TAS/STBC系统的误码率为1 × 10−3，d = 2λ，TAS/STBC系统的误码率为3 × 10−4，d = 3λ，TAS/STBC系统的误码率为2 × 10−4。这说明，随着天线间隔d的不断增大，信道相关性是逐渐变弱的，TAS/STBC系统的ASEP性能也是越来越好。
图6给出了TAS/STBC系统在不同的功率方位角谱的标准差下，使用QPSK调制方式，ASEP性能随总发射信噪比变化的曲线。功率方位角谱(PAS)的标准差σ分别取5˚、10˚、15˚。天线间隔d = λ，中心入射角θ0 = 20˚。由图6可知，当信噪比比较低时，三者的差距还是比较小，随着发射信噪比的增加，三者的差距是不断增大的。随着σ的不断增大，TAS/STBC系统在相关Rayleigh信道下的ASEP性能也是越来越好，例如，当信噪比为10 dB时，σ = 5˚，TAS/STBC系统的误码率为1 × 10−3，σ = 10˚，TAS/STBC
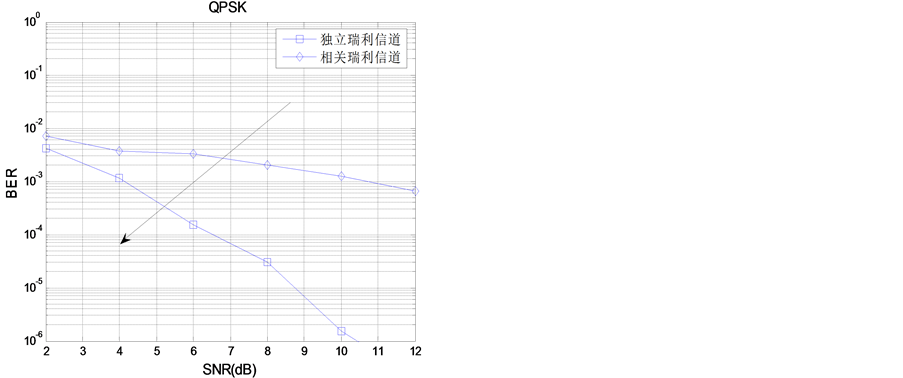
Figure 4. The ASEP performance of TAS/STBC system
图4. TAS/STBC系统的ASEP性能
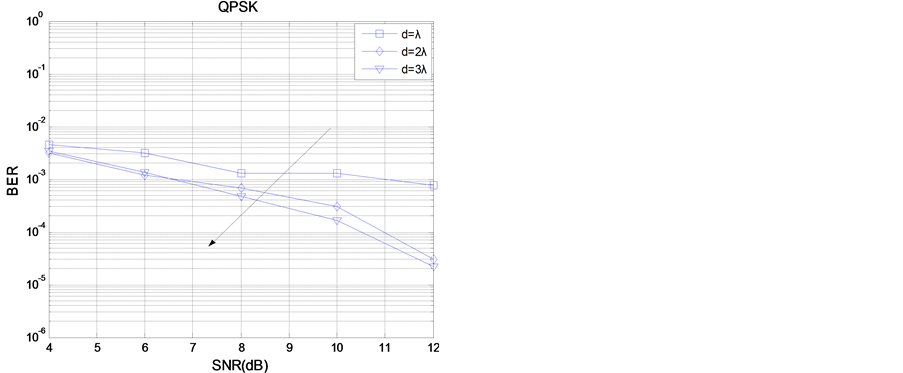
Figure 5. The effect of the antenna spacing on the ASEP performance of TAS/STBC system
图5. 天线间隔对TAS/STBC系统的ASEP性能的影响
系统的误码率为6 × 10−3，σ = 15˚，TAS/STBC系统的误码率为2 × 10−4。这说明，随着功率方位角谱(PAS)的标准差σ的不断增大，信道相关性是逐渐变弱的，TAS/STBC系统的ASEP性能也是越来越好。
图7给出了TAS/STBC系统在不同的中心入射角下，使用QPSK调制方式，ASEP性能随总发射信噪比变化的曲线。中心入射角θ0分别取20˚、40˚、60˚。天线间隔d = λ，功率方位角谱(PAS)的标准差σ = 5˚。由图7可知，当信噪比比较低时，三者的ASEP性能差距还是比较小；随着信噪比的增加，三者的ASEP性能差距是不断增大的，当θ0 = 40˚时，TAS/STBC系统的ASEP性能是最好的，当θ0 = 20˚时，TAS/STBC系统的ASEP性能要比其他二者差，例如，当信噪比为10 dB时，θ0 = 20˚，TAS/STBC系统的误码率为8 × 10−4，θ0 = 60˚，TAS/STBC系统的误码率为3 × 10−4，θ0 = 40˚，TAS/STBC系统的误码率为1.5 × 10−4；当信噪比为12 dB时，三者的ASEP性能差距又变得很小。
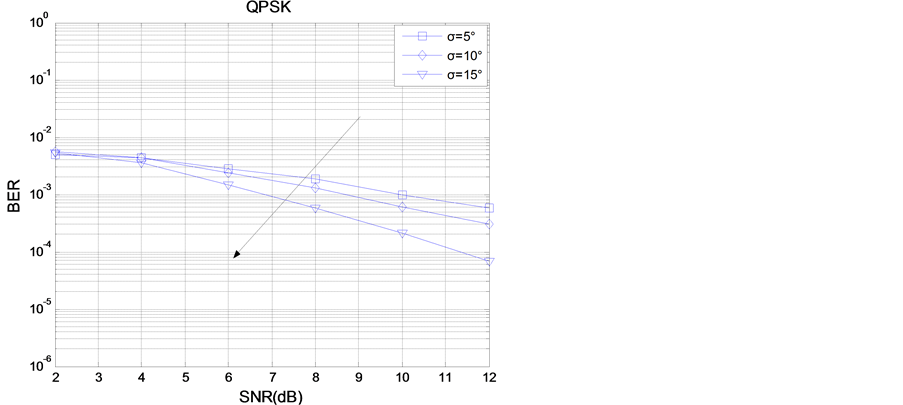
Figure 6. The effect of the PAS standard deviation on the ASEP performance of TAS/STBC system
图6. 功率方位角谱的标准差对TAS/STBC系统的ASEP性能的影响
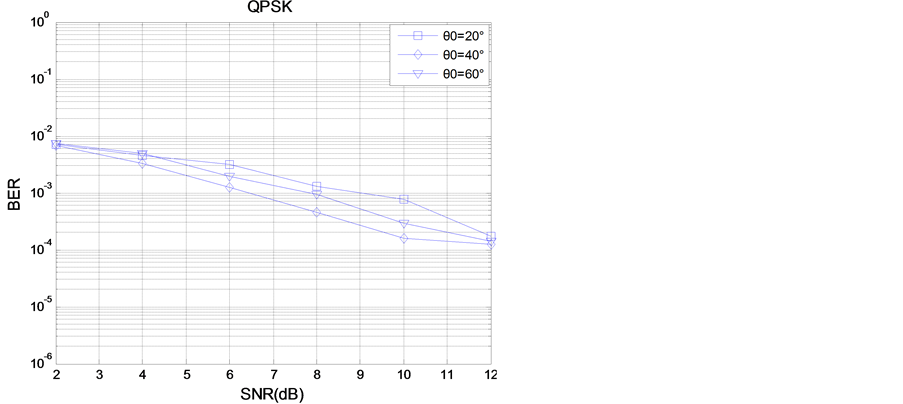
Figure 7. The effect of the mean AOA on the ASEP performance of TAS/STBC system
图7. 中心入射角对TAS/STBC系统的ASEP性能的影响
4. 结束语
本文首先采用了非常适合室内信道的Laplacian模型，得到了两个天线之间的相关系数，它是天线间隔，功率方位角谱(PAS)的标准差和平均到达角(AOA)三者的函数。然后引入了相关矩阵，建立了TAS/STBC系统的相关信道模型，基于等效的标量加性高斯白噪声(AWGN)信道的方法，得到了系统在接收端信噪比的表达式。最后研究了天线间隔，功率方位角谱(PAS)的标准差和平均到达角(AOA)三者对系统的ASEP性能的影响，并且做了仿真分析，仿真结果表明：随着天线间隔与功率方位角谱(PAS)的标准差的增大，以及选择合适的中心入射角，可以减小空间相关性，提高TAS/STBC系统的ASEP性能。
项目基金
青岛市国际科技合作项目(No. 12-1-4-137-hz)。