1. 引言
从20世纪30年代以来,生产自动化技术取得巨大成就,工业自动化涉及范围很广,过程控制是其中最重要的一个分支,工业生产对过程控制的要求是稳定性、安全性和经济性。过程控制的任务是在了解、掌握工艺流程和生产过程的静态和动态特性的基础上,根据上述三项要求,应用理论对控制系统进行分析和综合,最后采用合适的技术手段加以实现。在很多情况下,只需采用商品化的常规调节器进行PID控制就可以实现其控制任务。尽管在控制领域,不断涌现出各种新型控制器,但PID控制器还是以其结构简单、易实现、鲁棒性强等优点,在控制领域中处于主导地位,是工业过程控制的基础。根据日本有关调查资料显示,现今使用的各种控制技术中,PID技术站84.5%,优化PID控制技术占6.8%,现代控制技术占1.6%,人工智能技术占0.6%。如果把优化PID控制技术和PID控制技术加起来,那么PID技术占到整个控制技术的90%以上,有资料也指出,工业过程控制中,95%以上的回路具有PID结构[1] 。所以,可以毫不夸张地说,随着现代工业化和其他各种先进控制技术的发展,PID控制技术仍然不过时,而且还站着主导地位。
本文介绍了基于Microsoft Visual Studio 2010平台的VC的PID控制模块设计。可用于控制系统的仿真,控制器代码可以直接移植于目标系统。
2. 使用须知
纸型
PID控制器由比例单元(P)、积分单元(I)和微分单元(D)组成,是具有比例–积分–微分控制规律的控制器[2] 。当系统是连续控制时,其输入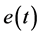 与输出
与输出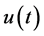 的关系为
的关系为
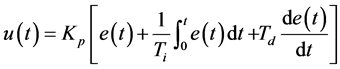 (1)
(1)
相应的传递函数为
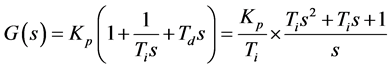 (2)
(2)
其中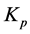 为比例系数;
为比例系数;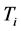 为积分时间常数;
为积分时间常数;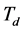 为微分时间常数。
为微分时间常数。
使用中只需设定三个参数(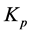 ,
,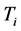 和
和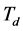 )即可。在很多情况下,并不一定需要全部三个单元,可以取其中的一到两个单元,但比例控制单元是必不可少的。各种控制作用(即比例作用、微分作用和积分作用)的实现在表达式(1)、(2)中表达得很清楚,相应的控制器参数包括比例系数
)即可。在很多情况下,并不一定需要全部三个单元,可以取其中的一到两个单元,但比例控制单元是必不可少的。各种控制作用(即比例作用、微分作用和积分作用)的实现在表达式(1)、(2)中表达得很清楚,相应的控制器参数包括比例系数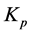 ,积分时间常数
,积分时间常数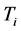 ,微分时间常数
,微分时间常数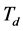 。
。
1) 比例控制
比例控制是一种最简单的控制方式,可以及时地反应控制系统的偏差信号,一旦系统出现了偏差,比例调节作用即产生调节作用,减小系统偏差的变化。具有比例控制规律的控制器,称为P控制器[3] 。P控制器实质上是一个具有可调增益的放大器,在信号变换过程中,P控制器只改变信号增益而不影响其相位。在串联校正中,加大控制器增益,可以提高系统的开环增益,减小系统稳态误差,从而提高系统的控制精度,但会降低系统的相对稳定性,甚至可能造成闭环系统不稳定。因此,在系统校正设计中,很少单独使用比例控制规律[4] 。
2) 积分控制
具有积分控制规律的控制器,称为I控制。I控制器的输出信号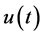 与其输入信号
与其输入信号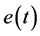 的积分成正比,即
的积分成正比,即
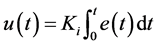 (3)
(3)
其中,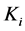 为可调系数。由于I控制器的积分作用,当其输入
为可调系数。由于I控制器的积分作用,当其输入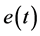 消失后,输出信号
消失后,输出信号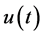 有可能是一个不为零的常量。
有可能是一个不为零的常量。
在串联校正时,采用I控制器可以提高系统的型别,有利于系统稳定性的提高,但积分控制使系统增加了一个位于原点的开环极点,使信号产生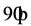 的相角滞后,不利于系统的稳定性[5] 。如果I控制器和之前提到的P控制器结合起来,便构成了具有比例–积分控制规律的控制器,称PI控制器,其输出信号
的相角滞后,不利于系统的稳定性[5] 。如果I控制器和之前提到的P控制器结合起来,便构成了具有比例–积分控制规律的控制器,称PI控制器,其输出信号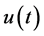 同时成比例的反应输入信号
同时成比例的反应输入信号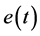 及其积分:
及其积分:
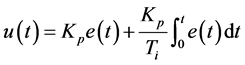 (4)
(4)
其中,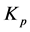 为可调比例系数;
为可调比例系数;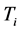 为可调积分时间常数。在串联校正时,PI控制器相当于在系统中增加了一个位于原点的开环极点,同时也增加了一个位于s左半平面的开环零点。位于原点的极点可以提高系统的型别,以消除或减小系统的稳态误差,改善系统的稳态性能;而增加的负实零点则用来减小系统的阻尼程度,缓和PI控制器极点对系统稳定性及动态过程产生的不利影响[6] 。只要积分时间常数
为可调积分时间常数。在串联校正时,PI控制器相当于在系统中增加了一个位于原点的开环极点,同时也增加了一个位于s左半平面的开环零点。位于原点的极点可以提高系统的型别,以消除或减小系统的稳态误差,改善系统的稳态性能;而增加的负实零点则用来减小系统的阻尼程度,缓和PI控制器极点对系统稳定性及动态过程产生的不利影响[6] 。只要积分时间常数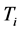 足够大,PI控制器对系统稳定性的不利影响可大为减弱。在控制工程实践中,PI控制器主要用来改善控制系统的稳态性能。
足够大,PI控制器对系统稳定性的不利影响可大为减弱。在控制工程实践中,PI控制器主要用来改善控制系统的稳态性能。
3) 微分控制
微分控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系,可以改善控制系统的响应速度和稳定性,微分作用能预见偏差变化的趋势,并能在偏差信号变得太大之前,在系统中引入一个有效的早期修正信号,反应系统偏差变化的规律,能产生超前的控制作用,从而加快系统的动作速度,减少调节时间。简单来说,微分作用能在偏差还没有形成之前,就可以消除误差,改善系统的动态性能[7] 。
微分作用取决于微分时间常数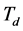 ,
,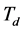 越大,控制器的微分作用表现得就越强,
越大,控制器的微分作用表现得就越强,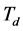 偏大时,超调量会较大,调节时间也会较长;
偏大时,超调量会较大,调节时间也会较长;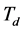 越小,控制器的微分作用越弱,
越小,控制器的微分作用越弱,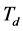 偏小时,超调量也较大,相应调节时间也会较长;
偏小时,超调量也较大,相应调节时间也会较长;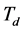 调节合适时,系统的超调量和调节时间可以有效的减小。微分作用反映的是输入信号的变化率,当偏差没有变化时,微分作用的输出为零。此外,从滤波器角度来说,微分控制器相当于一个高通滤波器,对噪声干扰有放大作用,这对系统是非常不利的,因此我们就不能过多的增加微分调节[8] [9] 。
调节合适时,系统的超调量和调节时间可以有效的减小。微分作用反映的是输入信号的变化率,当偏差没有变化时,微分作用的输出为零。此外,从滤波器角度来说,微分控制器相当于一个高通滤波器,对噪声干扰有放大作用,这对系统是非常不利的,因此我们就不能过多的增加微分调节[8] [9] 。
3. 数字PID控制器
PID控制器是控制系统中应用最为广泛的一种控制器,广泛应用于工业过程控制中。随着微型计算机,特别是现代嵌入式位处理器的普及应用,原先由硬件实现的PID控制器的功能都可以用软件来代替实现,形成数值PID算法,实现由模拟PID控制器到数字PID控制器的转变。
在实际应用中,数字PID控制器分为两种:位置式PID控制器和增量式PID控制器。
3.1. 位置式PID控制器
计算机实际上是采样控制,它根据采样时刻的偏差值计算控制量。所以式(1)中的积分项和微分项不能直接使用,需要进行离散化处理。具体实现方法是:以K作为采样信号,T作为采样周期,则连续时间对应离散化的采样时间KT,用求和的形式代替积分,用增量的形式代替微分,则可作如下的近似变换:
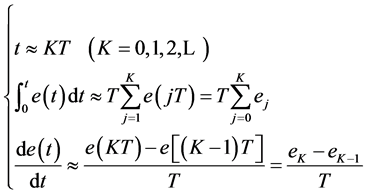 (5)
(5)
将式(5)代入式(2)中,则得到离散的PID控制器表达式为:
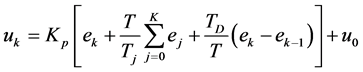 (6)
(6)
或:
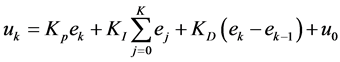 (7)
(7)
式中:
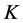 ——采样序列号,
——采样序列号,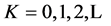 ;
;
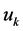 ——第
——第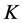 次采样时刻计算机输出值;
次采样时刻计算机输出值;
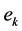 ——第
——第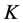 次采样时刻的输入偏差值;
次采样时刻的输入偏差值;
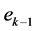 ——第
——第 次采样时刻的输入偏差值;
次采样时刻的输入偏差值;
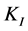 ——积分系数,
——积分系数,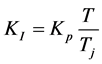 ;
;
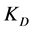 ——微分系数,
——微分系数,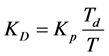 ;
;
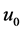 ——开始进行PID控制时的计算机的输出值。
——开始进行PID控制时的计算机的输出值。
因此,如果采样周期足够小的话,那么由式(6)和(7)得到的近似结果可获得足够的精确度,此时连续的和离散的PID控制过程会十分接近。由于式(6)和(7)的控制算法是直接按式(1)给出的PID控制规律进行计算的,所以给出了全部控制量的大小,被称为全量式或位置式PID控制算法[10] 。
由于位置式PID控制器每次输出全部控制量,因此它可以直接作用于执行机构。另一方面,由于这种算法全量输出,每次输出均与过去的状态有关,计算时要对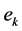 进行累加,容易造成积分饱和,计算机运算工作量很大;此外,因为计算机输出的
进行累加,容易造成积分饱和,计算机运算工作量很大;此外,因为计算机输出的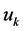 对应的是实际的执行机构的位置,如果计算机出现故障,
对应的是实际的执行机构的位置,如果计算机出现故障,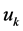 大幅度变化,这将会引起执行机构位置的大幅度变化,可能造成重大生产安全事故。这就导致这种算法不适用于生产实践中,催生了增量式PID控制器算法。
大幅度变化,这将会引起执行机构位置的大幅度变化,可能造成重大生产安全事故。这就导致这种算法不适用于生产实践中,催生了增量式PID控制器算法。
3.2. 增量式PID控制器
增量式PID控制器是指PID控制器每次输出的只是控制量的增量,当例如步进电机等执行机构,需要的是增量而不是位置量的绝对数值时,就可以使用增量式PID控制器进行控制。
由式(7),根据递推原理可得:
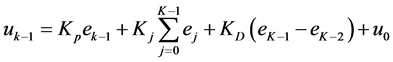 (8)
(8)
用式(8)减去式(7)可得:
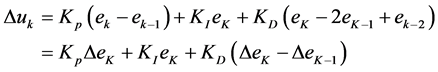 (9)
(9)
式中,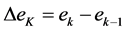 。
。
式(9)称为增量式PID控制算法。将该式整理合并得到:
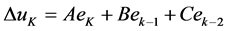 (10)
(10)
式中,
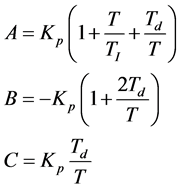
它们都是与采样周期、比例增益、积分时间常数和微分时间常数有关的常系数。
根据增量式PID算法可以推导出位置式PID算法的递推形式,其表达式为:
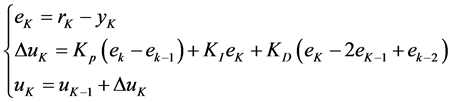 (11)
(11)
其中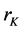 为系统的输入,
为系统的输入,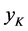 为控制对象的测量量。
为控制对象的测量量。
位置式PID控制器实质上与增量式PID控制器是一样的,但是增量式PID控制器比位置式PID控制器有许多优越之处[11] :
a)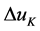 只与
只与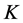 ,
, ,
,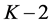 时刻的偏差有关,节省运算时间和内存。
时刻的偏差有关,节省运算时间和内存。
b) 每次只做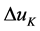 计算,则计算误差影响很小。
计算,则计算误差影响很小。
c) 由于每次只输出增量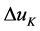 ,因此误动作产生的误差很小,并便于实现无扰动切换。
,因此误动作产生的误差很小,并便于实现无扰动切换。
鉴于增量式PID控制的种种优点,本论文采用增量式PID控制来进行仿真。
3.3. 增量式PID控制的算法实现
应用中,增量式PID控制器的算法实现如图1所示。
4. Stehfest算法
对于函数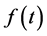 定义其拉普拉斯变换为:
定义其拉普拉斯变换为:
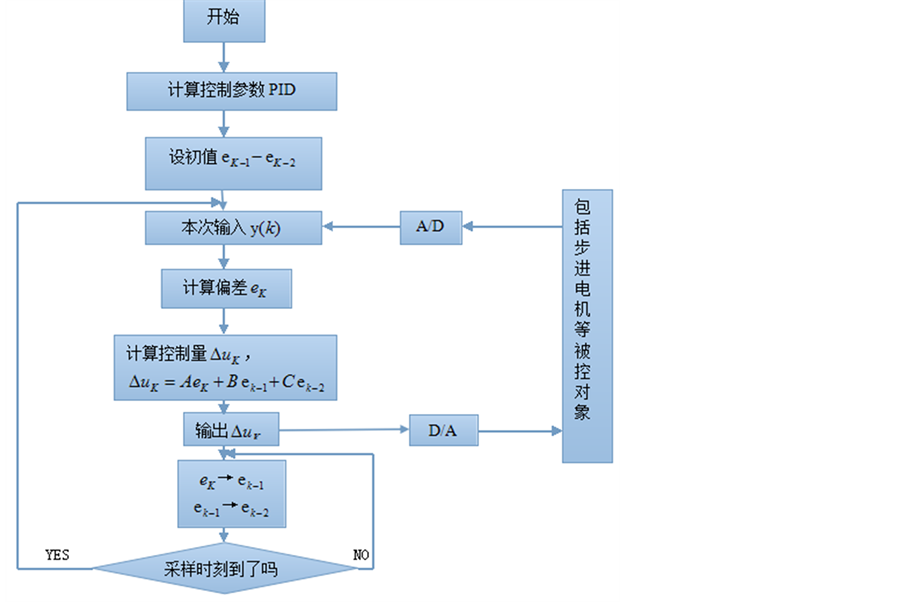
Figure 1. Block diagram of incremental PID
图1. 增量式PID实现框图
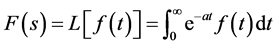 (12)
(12)
称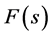 为函数
为函数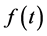 的拉普拉斯变换像函数。在VC中要实现对控制系统的输出值的计算,需要将S 域的拉普拉斯表达式
的拉普拉斯变换像函数。在VC中要实现对控制系统的输出值的计算,需要将S 域的拉普拉斯表达式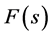 转换为时域的函数表达式
转换为时域的函数表达式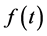 ,则需要拉普拉斯反变换。
,则需要拉普拉斯反变换。
目前经常使用的反变换法有部分分式展开法和围线积分法。当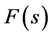 表达式比较复杂时,这两种方法都很难实现反变换。这时就需要采用一种新的算法来实现拉普拉斯反变换。Stehfest算法就是这样的一种拉普拉斯反变换的近似算法。
表达式比较复杂时,这两种方法都很难实现反变换。这时就需要采用一种新的算法来实现拉普拉斯反变换。Stehfest算法就是这样的一种拉普拉斯反变换的近似算法。
采用围线积分法实现反变换时,需要计算被积表达式在各极点上的留数。但当表达式比较复杂或存在多重极点时,微分运算用手工实现比较困难;借助计算机运算时,由于数值微分算法具有天生的数值不稳定性,又使运算误差不易控制。Stehfest算法用一个全新的表达式代替围线积分法中的积分式,可在计算机辅助下近似实现拉普拉斯反变换,其形式如下:
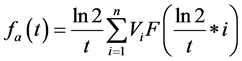 (13)
(13)
其中
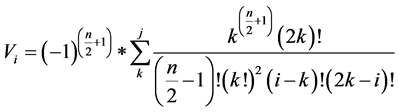 (14)
(14)
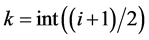 (15)
(15)
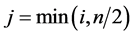 (16)
(16)