1. 引言
平面径向流是渗流力学[1] 中的基本问题，也是水气藏和油气藏等相关问题的重要基础。经典渗流力学采用连续介质理论，对微分方程在定解条件下进行求解，实际工程问题则是通过建立神经网络[2] 、半球向心流[3] 等模型来解决问题。
本文利用拓扑网络模型[4] ，对有界平面径向流问题进行数值模拟，最终得到流动图像和压力分布图像。这样，我们既能得到流动的具体过程，又能直观的看到流动方式和参数变化，而这是其它方法所不具备的。同时，进一步说明拓扑网络模型能较好的描述细观渗流问题。
2. 拓扑网络模型
2.1. 模型简介
多孔介质分为骨架和孔隙。我们将孔隙部分简化为管道和节点，忽略孔隙的具体空间形状，孔隙部分按一定规律分布于骨架中，以此构成拓扑网络模型，其中骨架部分不参与流动，直接简化为网络以外的部分。
拓扑网络模型由管道和节点组成，管道内的流动均为管流。
2.2. 模型设定
我们把管道分为大管和小管，二者随机分布于模型中。大管管径为10，小管管径为5，且所有管道的管长均为100。本文用大小为100 × 100的网络模型进行模拟。t = 0时，模型中充满气体且气体压强为10，在节点(51, 51)处施加大小为20的压力，这样液体就在压力的作用下从节点(51, 51)处开始渗透。在这样的压力设定下，所有的流动均为层流。
液体的流动速度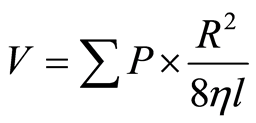
[5] ，其中η = 0.8937 × 10−3，R为管径，
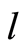为管长，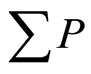
为水头两侧压差。随着液体的流动，压力会渐渐减小，压降
。
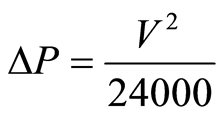3. 数值模拟思想
我们建立100 × 100的拓扑网络模型，模型包括横向管道、竖向管道和节点，三者均用数值矩阵表示。管道和节点的各种状态和性质分别用数值表示在矩阵中，比如大管为1，小管为0。各节点的压力大小也用数值矩阵表示。液体流动产生的压降和气体压缩都会导致水头压力下降，所以液体每走一步就重新计算压力矩阵。
液体在流动过程中，由于流动路径和水头压差的不同，流动的快慢也不同，这样会有气体被液体封堵在管道中，形成死气区。对节点数值矩阵进行二值化填充处理，就可对死气区进行提取。
4. 数值模拟结果
4.1. 流动图像和压力分布变化过程
我们设定大管比例为55%，小管比例为45%。
图1和图2分别为液体流动图和压力分布变化图。图1表示液体从注入点渗入多孔介质后的情形，图2表示液体在流动过程中的压力响应，可以看出在注入点附近压力梯度较大，而离注入点越远的区域，压力梯度越小。我们还可以看到液体渗透的过程中，气体逐渐被压缩，压力逐渐增大，当气体压力与水头压力相等时，渗透过程达到稳态。
图3为压差变化曲线。在节点(51, 51)点左右进行压差计算，得到图中蓝色曲线，通过拟合得到红色曲线。图中曲线与经典渗流力学中的压降漏斗相吻合。
4.2. 压力大小对渗透的影响
液体在多孔介质中渗透的过程，就是水头在压力作用下在管道中流动的过程，改变水头的压力会影响整个流动过程。本文在层流的范围内讨论压力大小。
图4中的三幅图分别是大管比例为55%，注入点压力为15、20、25的压力分布图。
我们可以看出，当注入点压力增大时，液体渗透范围增大，压力梯度增大。死气区的数目分别为50、63、67，逐渐增多。
4.3. 死气区
在液体渗透的过程中，多孔介质的非均匀性和液体粘性都可能导致指进现象。指进的液体在特定的
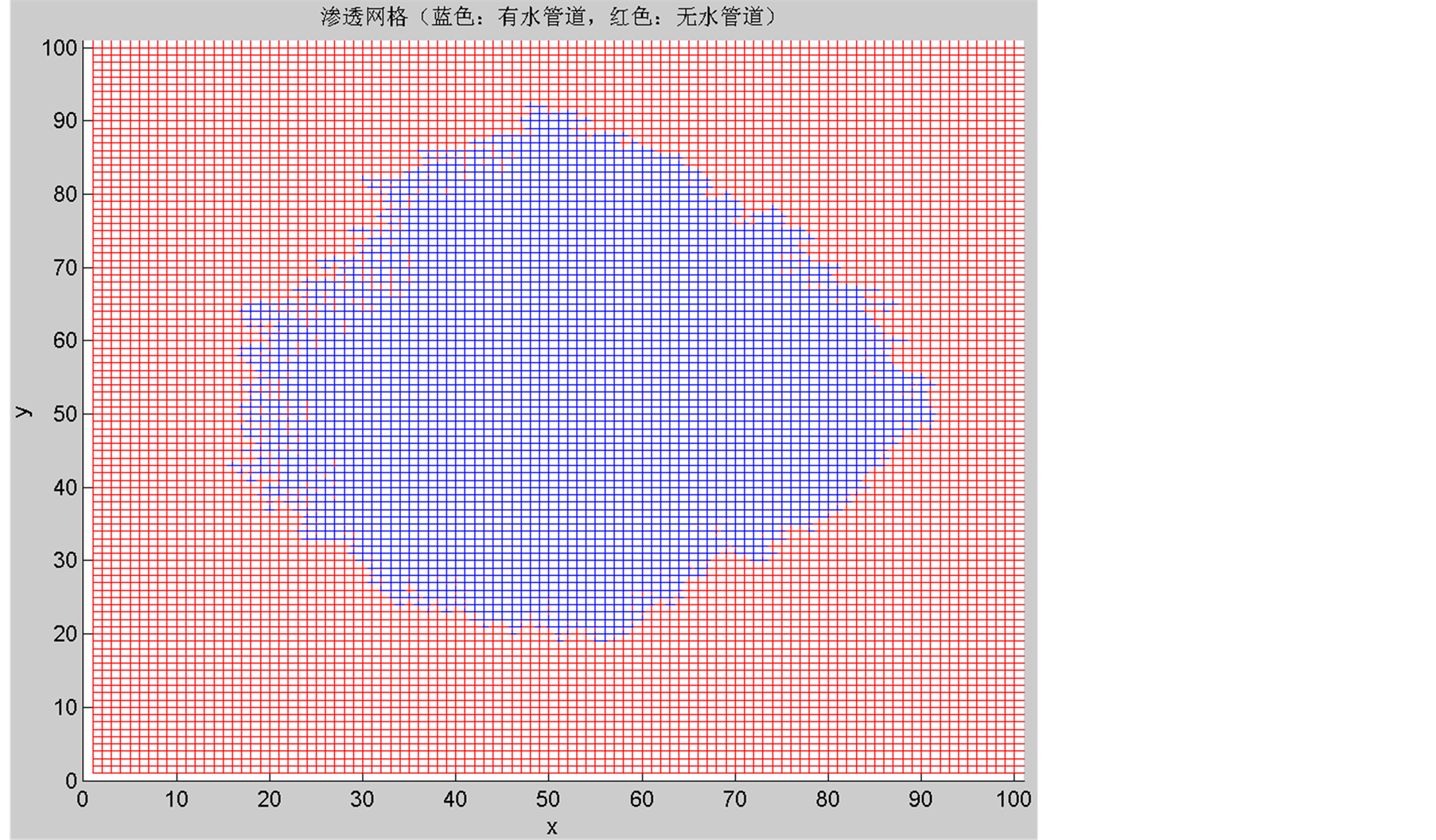
Figure 1. Flow image
图1. 流动图像
情况下可能把气体封堵于局部区域，这样就形成了死气区。
图5中的三幅图分别为大管比例55%、65%、75%条件下的压力分布图，可以看出死气区无规律的分布于有水区域。在注入点附近，由于压力较大，气体很容易被液体挤压出去，不容易存留，所以死气
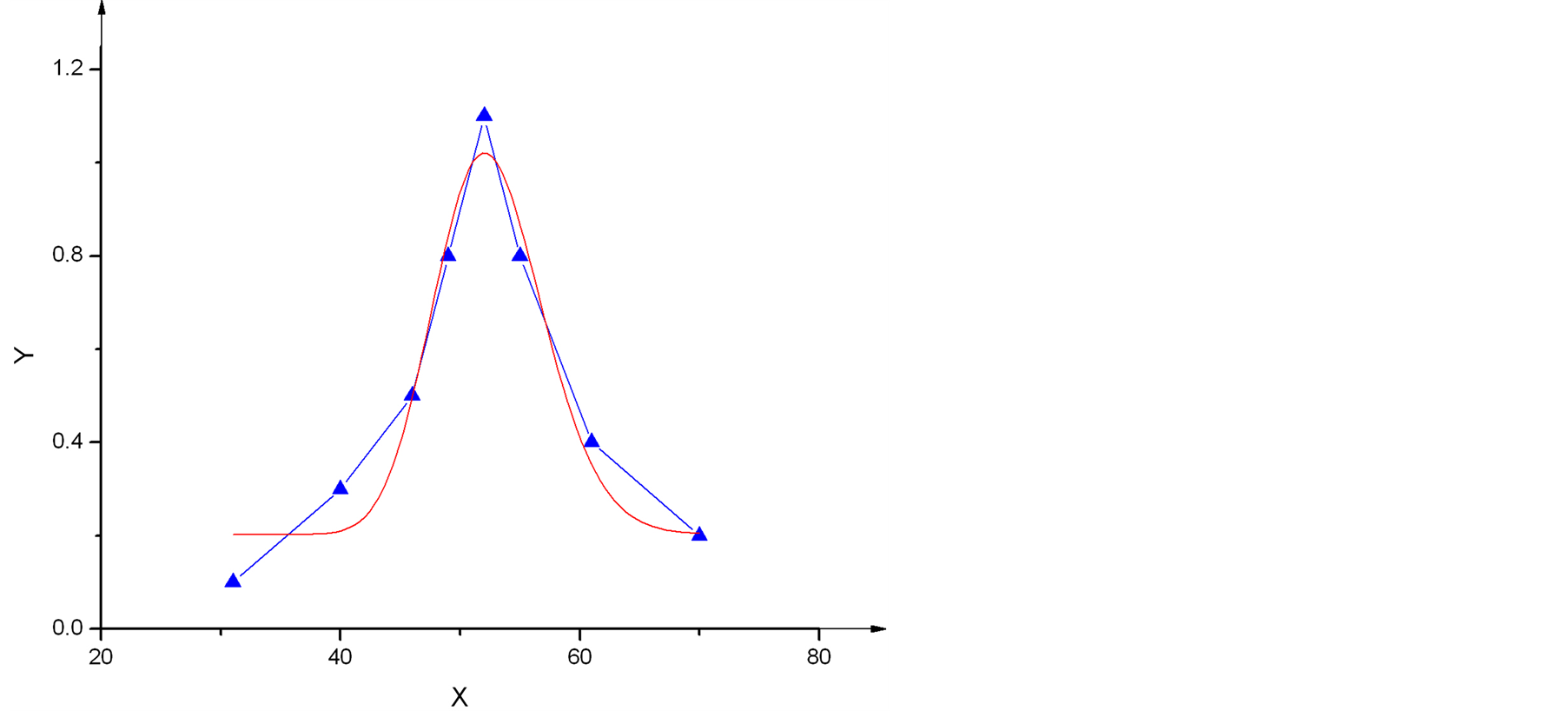
Figure 3. The radial pressure distribution curve
图3. 压力径向分布曲线
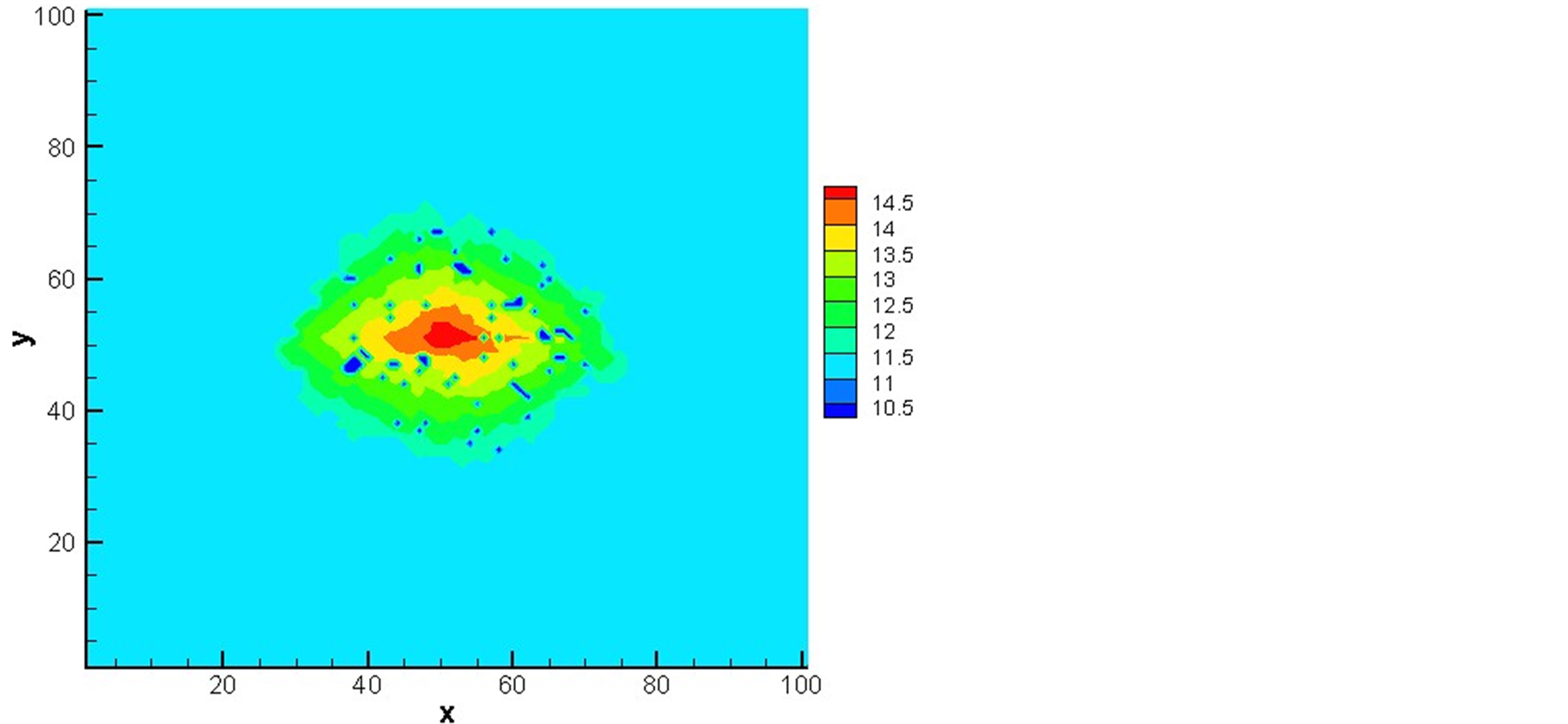
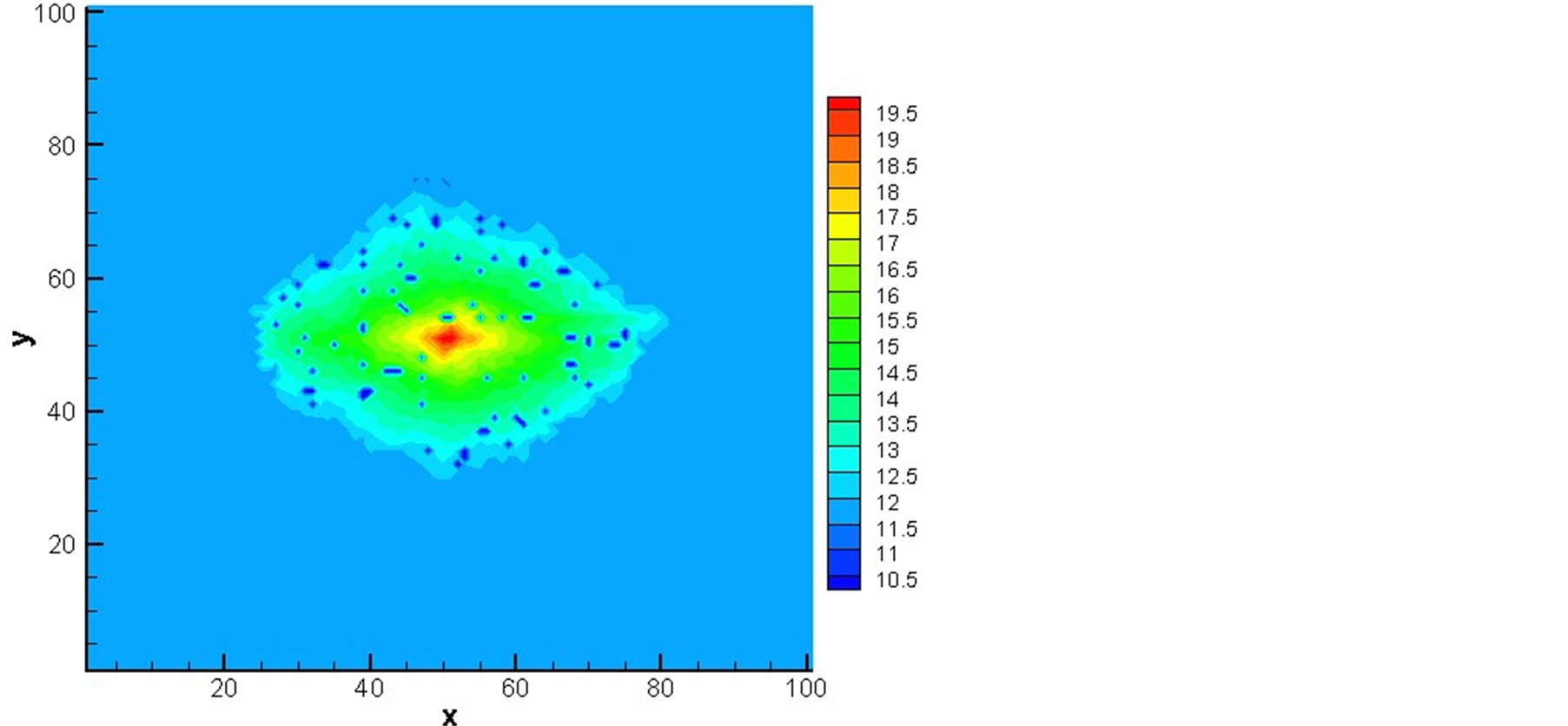
Figure 4. Pressure profile image
图4. 压力分布图
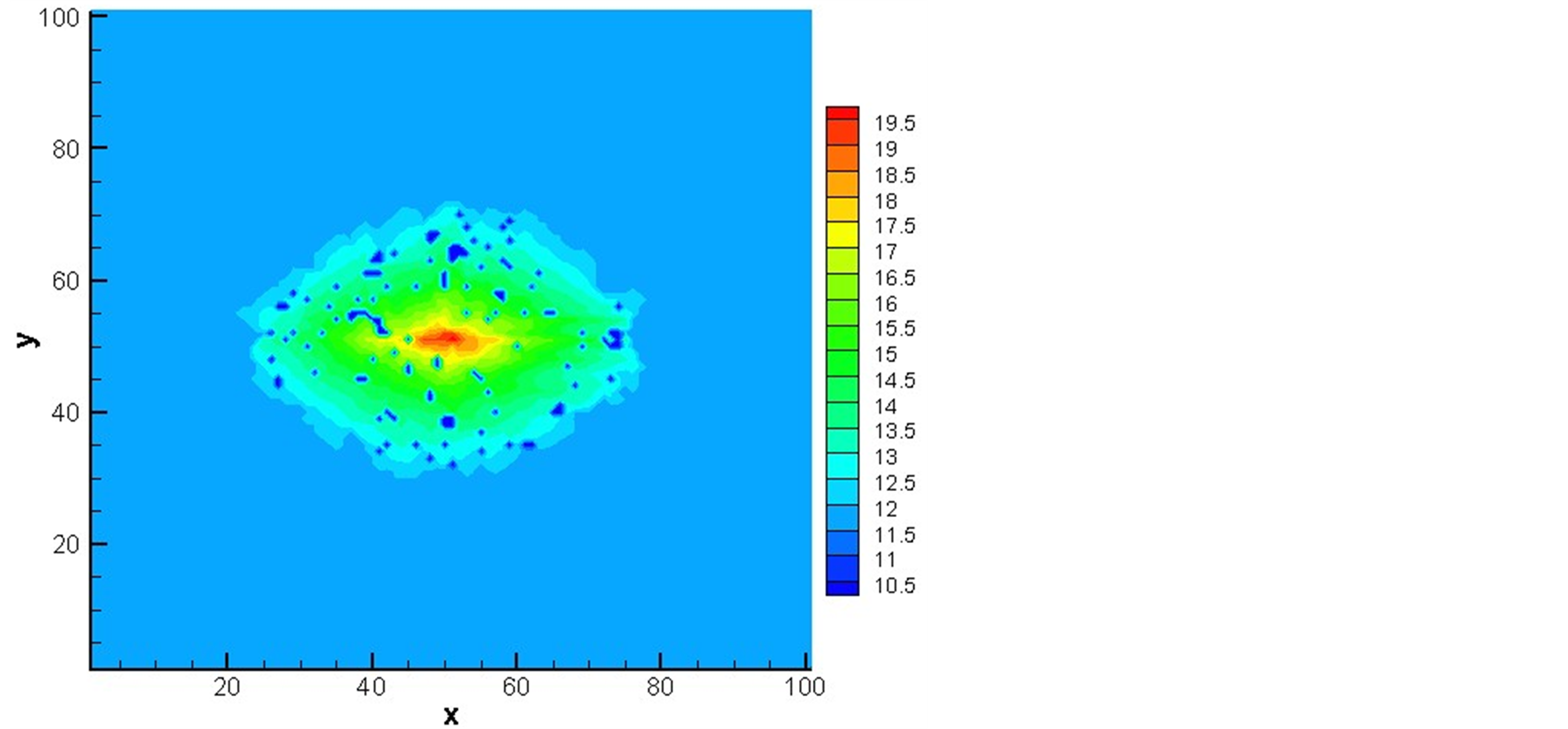
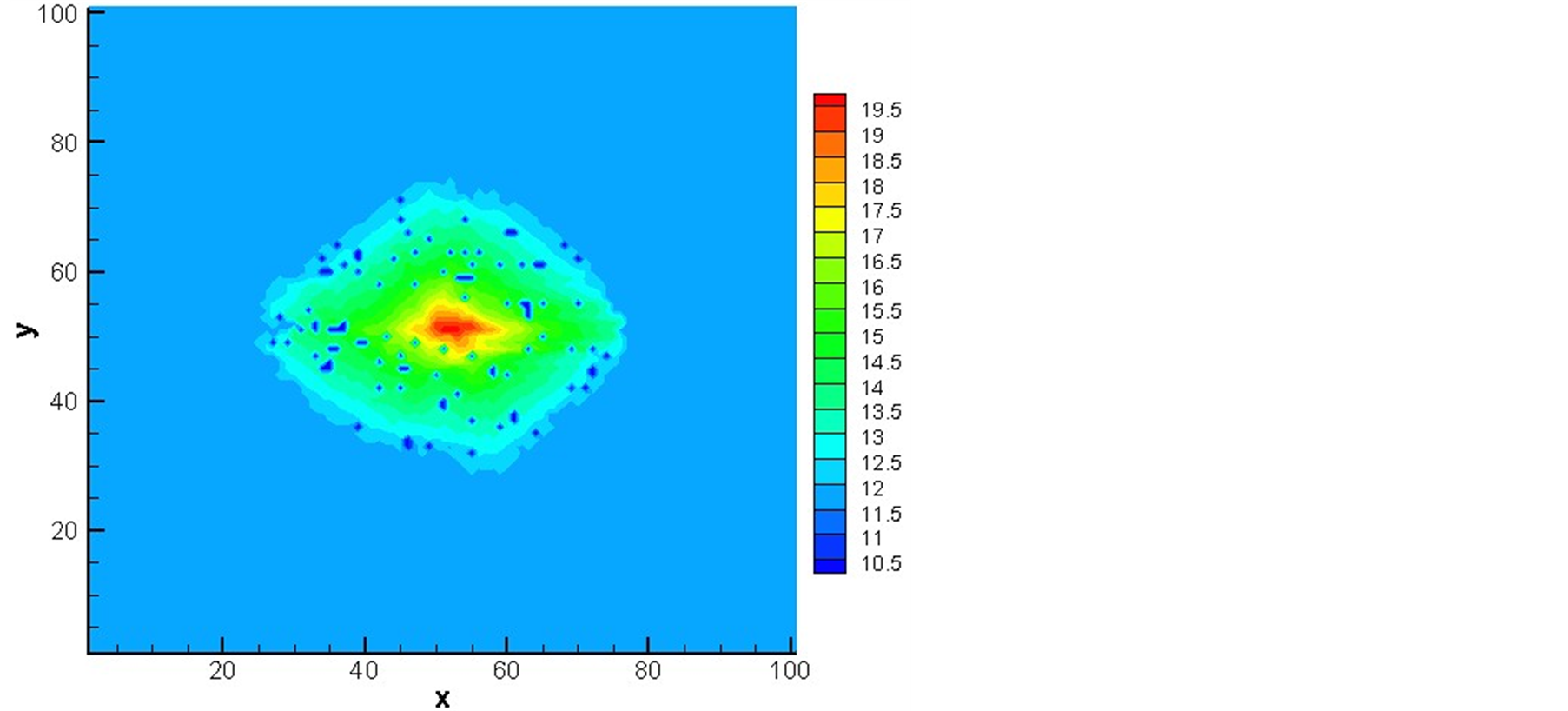
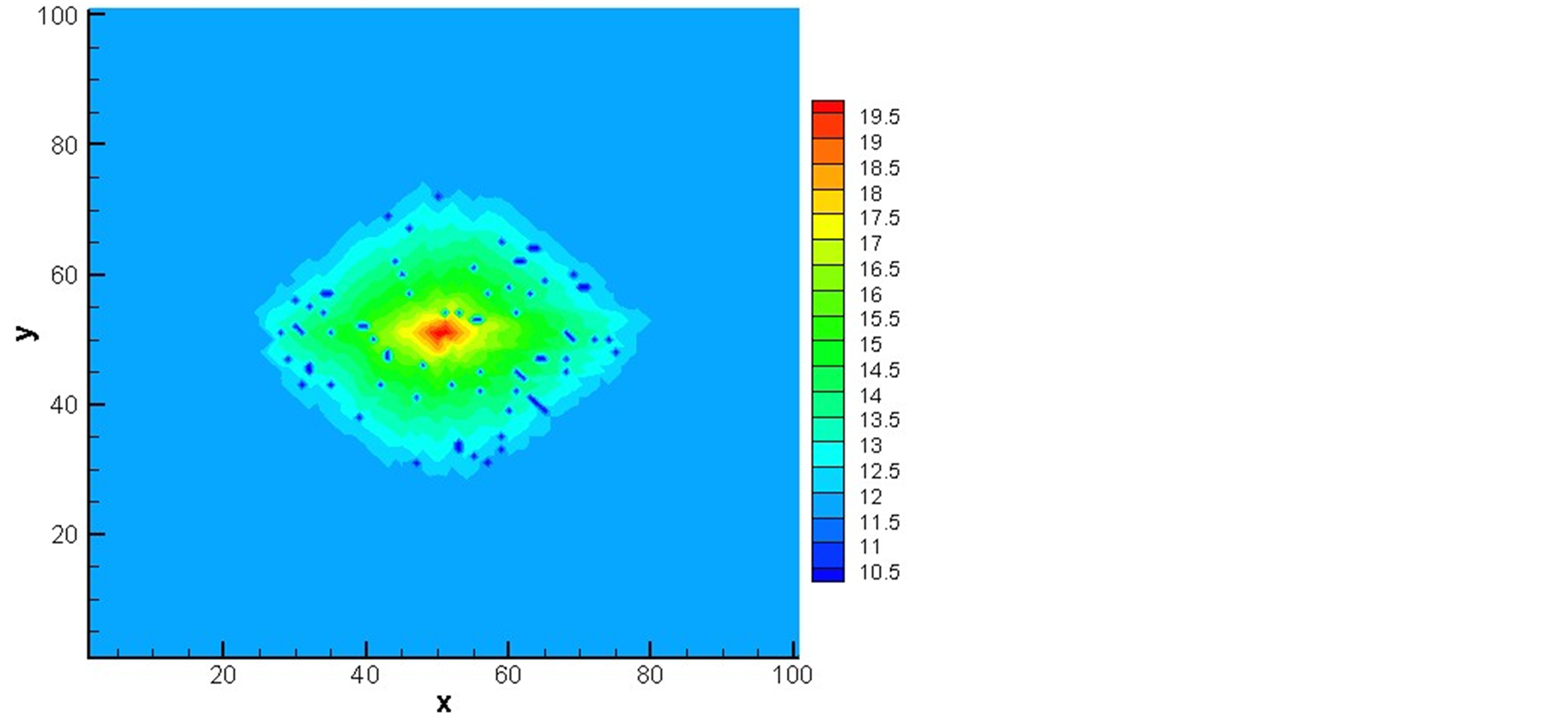
Figure 5. Pressure profile image
图5. 压力分布图
区数量较少。通过多次计算得到随着大管比例的增加，死气区数目有逐渐减小的趋势，这是因为大管比例较大时，多孔介质结构更为简单，气体更容易挤压出去；当大管和小管比例接近时，多孔介质结构复杂，而大管流速比小管快，更容易出现指进现象，即更容易形成死气区。
一般情况下，粘性指进是粘度小的流体驱替粘度较大的流体时产生的一种不稳定界面现象。而本文发现，在有压的条件下，粘度大的液体驱替粘度小的气体时，也可能出现指进现象。
5. 结论
本文通过数值模拟得出两相有界平面径向流的流场和压力分布，与经典结果相符，表明拓扑网络模型的合理性。本文还得到压力分布图像和变化过程，这可以具体、直观的展示和分析结果，是拓扑网络模型独特的优势。
通过对数值模拟结果进行分析，本文得出多孔介质非均匀性可以导致指进，拓展了粘性指进的范畴。
本文研究和探讨了可能影响死气区的各种因素。我们发现，压力越大死气区越多；大管和小管比例越均衡，死气区越多。
拓扑网络模型还可以用来研究许多渗流问题。例如，如果能够把油水两相在管道中的复杂作用进行合理的简化和转换，该模型也可拓展应用于水驱油等更复杂的情形。