1. 引言
时间延迟估计[1] 是表征一个信号的基本参量，自1976年起，Knapp和Carter发表了有关互相关的时延估计的论文[2] ，从此对时间延迟及其有关的参量的估计成为了信号处理领域中活跃的研究方向。
广义二次互相关算法[3] 提高了时延估计的精度。广义二次互相关时延估计已经在无线定位中实现应用[4] ，无线电定位技术通常使用的到达时间(Time of Arrival, TOA)、到达时间差(Time of Difference Arrived, TDOA)已经被应用在IS-95 CDMA和GSM[5] 中。
在时延估计中，使用传统的权值进行时延估计会出现峰值偏移、多峰值和大噪声下信号淹没，本文提出了一种新的权值估计，主要是针对信号的偏移、多峰值和大噪声情况进行改进。考虑到小功率信号在传统的权值算法恢复出来的精度大大降低，通过改进的权值来提高小功率信号在低信噪比条件下的估计精度。
2. 二次相关延迟估计方式
2.1. 一次互相关
假设信号模型为
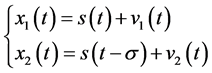(1)
其中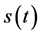
是信号源发送的信号；
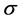是延迟的时间；
、
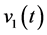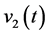为互不相关加性噪声。
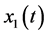为基站发送信号，
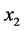为接收点接收到的信号，
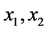的互相关函数为：
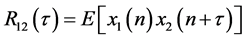(2)
把公式(1)代入公式(2)有
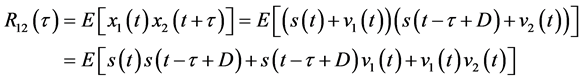(3)
(3)式可写为：
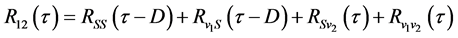(4)
式中
为发送信号和接受信号的互相关函数，
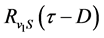为发送信号和噪声的互相关函数，
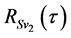为接收信号中噪声的互相关函数，
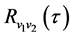为噪声的互相关函数，若加性噪声是理想的非相关高斯白噪声，信号和噪声、噪声和噪声之间的互相关，则：
由相关函数的特点，当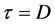
时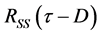
取得最大值，即相关函数
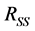的峰值点对应的时间点就是时间延迟点。但是因为加性噪声不一定是理想的高斯白噪声，时间观察信号的时间也不可能无限长，所以式(5)、(6)、(7)并不严格为零。当信噪比较大时，或满足不相关时，上述三式的影响不能忽略。所以在文献[6] 中提出了二次互相关算法。
2.2. 二次互相关
在基本互相关时延估计算法的基础上，文献中提出了一种基于二次互相关时延估计算法。该算法先对信号进行自相关和互相关运算，然后利用得到的自相关和互相关函数，在进行相关运算，提高信号信噪比与分辨率。
二次互相关算法的基本流程图，如图1所示。
二次互相关计算过程首先发送信号做自相关计算得到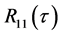
，接收信号和发送信号通过互相关得到
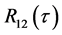，在对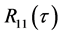
、
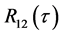进行二次互相关，得到的结果为
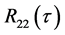，对二次互相关加权得到功率函数谱密度，通过傅里叶反变换估计出时延。
二次互相关算法首先求两个信号之间的互功率谱，然后在频域内给予加权，以此来对信号和噪声进行白化处理，从而增强信号中信噪比较高的频率成分，抑制噪声的影响，最后通过反变换得到时域值，两个信号之间的广义互相关函数为：
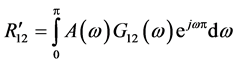(8)
式(8)中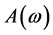
为权值函数，广义互相关加权函数的选择主要是基于噪声和反射情况。根据不同的情况选择不同的权函数，目的是为了使
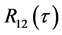具有比较尖锐的峰值。
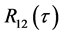的峰值即为两个基站之间的时延。
3. 不同窗函数
来自同一个信号源的经过环境中的反射、绕射的多路信号存在一定的相关性，通过计算不同的节点
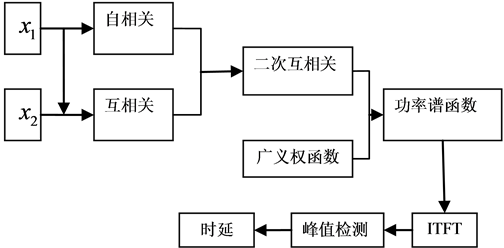
Figure 1. Second correlation of TDE process
图1. 二次互相关流程图
接收到的信号之间的互相关函数就可以估计出TDOA值或者通过计算发出的信号返回来的信号可以计算TOA值。在实际的环境中，由于噪声和混响的影响，相关函数的最大峰会被弱化，有时还会出现多个峰值，这些都会影响实际峰值的检测。GCC法就是在功率谱域对相关信号进行加权，突出相关信号部分并且抑制受噪声干扰的部分，以便使相关函数在时延处更为突出便于得到更好的时延估计。但是，由于混响的存在使得信号中包含了多个回波分量，此时计算出的互相关函数就会包含直达波和反射波，这些都会对互相关计算带来很到的影响使检测比较困难。为了使时延估计不受信号本身特性的影响，并且尽可能的抑制混响和噪声，需要对信号的频谱做特殊的处理即加权处理。
一个较好的权值会对整个的互相关时延估计有很大的影响。在时延估计中不仅仅是体现在波峰的突出上面，还要考虑到时延估计的精确度。
传统的时延估计在加权时大部分使用的是平滑相干变换窗[7] 、CC、最大似然窗、ROTH、SCOT、PHAT窗[3] ，这些窗函数基本特性如下：
基本窗函数(CC)权值为1，基本权值对外围噪声、反射比较敏感，在使用时误差较大[8] [9] ，在时延
估计中几乎不会使用基本权值；ROTH加权，表达式为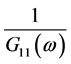
，等价于维纳滤波，可以有效抑制噪声大的频带，但会展宽相关函数的峰，ROTH加权会出现多个峰值不容易辨识真正的峰值；SCOT表达式为
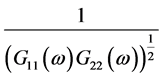，主要特点可以有效的抑制大噪声的频带，与ROTH权值相比较SCOT加权考虑到两个通道的影响，缺点是会展宽互相关函数的峰，信噪比较大时会出现峰值偏移；改进的SCOT权值，表达式为
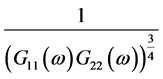，主要功能和SCOT一样，但是可以避免环境中的回响而导致虚假的峰值，缺点和SCOT加权相同；PHAT权值表达式为
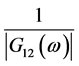，在信号功率较大的情况下能够很好的得到时延估
计，与上述权值相比在相同的环境下能够更好的得到峰值，缺点是在信号能量较小时分母会趋于零，从而会加大误差，常见的一些改进方法考虑到分母中加入一个固定的常数，但是这个固定的常数不能够随信号能量的变化来进行改变，这样对信号的敏感度比较低。
上述权函数中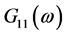
为发送信号的自相关功率谱密度，
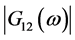为发送信号和接收信号的互相关功率谱密度。上述的权函数得到的互相关时间估计的最大特点是简单，并且默认的信号和噪声以及噪声和噪声之间是互不相关的，在实际中这点是不能满足的。另外这样定义的互相关函数是严格意义上的统计或者是在平稳遍历的以无穷时间平均代替的数学平均。在实际中，这种严格的数学平均和无穷时间的平均是不可能做到的。
在上述的窗函数中PHAT较好但是在小功率信号中会有很大的偏移，CC、ROTH、SCOT会出现多个峰值。无线信号往往会使用小功率信号发送信息。为克服以上缺点，本文中提出新的窗函数的表达式为：
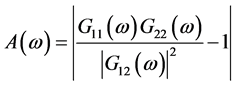(9)
这里的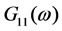
为发送端的信号自相关功率谱，
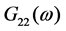为接收信号的自相关功率谱，通过改进的权函数可以更好的抑制大噪声，运用小功率信号的广义互相关求时延。
本文中的提出的加权函数代入式8重新加权计算得到
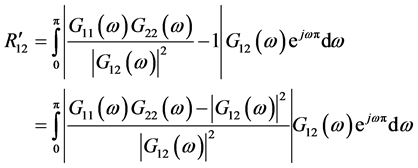(10)
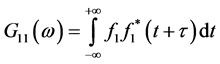(11)
式(10)为本文提出权值函数重新加权推导计算，式(11)为发送信号自相关计算，同样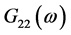
、
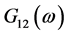也是通过(11)式计算得到，通过
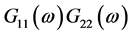兼容了SCOT加权函数的特性用来回避环境中的回响和虚
假峰值，通过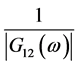
加权函数用来抑制大噪声频带。本文提出的加权函数用于能量较小的信号，在信
号能量较小时SCOT加权函数、ROTH加权函数以及PHAT加权函数由于信号能量较小峰值波动较小在加上外在噪声的影响很难检测到时延，特别是SCOT加权函数和ROTH加权函数，在信号能量较小外在噪声大时仅仅通过一个信道检测将会有很大的偏移，在SCOT加权函数时虽然考虑到双信道，功率谱加权的为互相关函数那么在这里将会将会出现误差产生虚假峰值和频带展宽现象。若使用PHAT加权函数加权如果信号能量较小时分母会趋于零，会加大误差。本文提出的权值是在此基础上提出，增加时延估计的精度。
ROTH权值是仅仅使用了一个自相关进行加权没有考虑到接收信号或者发送信号的影响，相比较ROTH信号本文提出的权值兼顾发送信号和接收信号同时会影响时延估计，所以在权值中既有发送信号的功率谱密度也有接收信号的功率谱密度。相对于SCOT互相关函数的峰值通过分母中的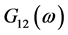
进行抑制。在大信号情况下PHAT权值函数能够较好的得到较高的精确估计，但是能量较小的信号分母会趋于零，所以通过改进的权函数能够有效的改进PHAT在能量较小的情况下得到更高精确度的时延估计。
本文对权值的计算考虑到分母会随着信号能量的减小而减小，在分子中加入发送信号和接收信号的自相关是为了抑制分母减小时会出现较大的误差，分子中的数值随着信号能量的减小也逐渐减小，这样可以减小加权的误差以便提高信号时延估计精度。
本文提出的窗函数完善PHAT函数，在PHAT权函数中分子始终是定常数，PHAT在大功率信号时PHAT权值估计精度比较高，但是在小功率信号时信号能量小将会导致分母趋于零，使得误差变大，所以对PHAT进行改进时通常需要在分母上加一个常数，这个常数项在某一个小功率信号区间会有一定的改进，而无线通信中信号是未知的并且接收到的信号能量大小和距离基站的位置有很大的关系，所以信号能量不是一个固定的范围，在分母中加入一个常数项是远远不能使PHAT权值适用整个的系统的时延估计，在这时需要通过自适应性来对信号强度进行匹配，但是使用自适应性对信号匹配导致算法比较复杂并且硬件实现是比较困难。改进的权函数为了更好的适应信号的强度，在分子中加入了信号的自相关函数，在小功率信号的情况下，信号的自相关系数也会随之变小，使得在小功率信号下分母在逐渐变小的同时分子也在逐渐减小，通过分子分母的比例得到的权函数加入到峰值估计中可以提高对信号估计的精度，这样会使权函数能够更好的适应环境，同时提高对信号的估计精度。
4. 仿真分析
通过Matlab进行仿真计算令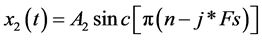
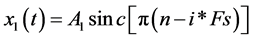这里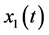
、
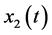表示两个传感器接收到的信号，再分别加高斯白噪声，假设噪声信号与信源信号之间，噪声与噪声之间相互独立。为了便于仿真假设两个信号之间的噪声相同。本文中所指的大功率信号是指的信号的幅值大于1时，小功率信号是指信号幅值在0.000001以下的信号。
4.1. 大功率信号仿真
当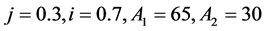
，Fs为一个定常数，在仿真中我们选择为200。信噪比为0 dB时仿真如图2所示。
如图2中所示，在信噪比为0 dB时，不同权值仿真都能够较为精确的得到时延，ROTH、基本权值、PHAT权值和改进的权值互相关函数的峰值比较突出，尖锐程度较好。
在信噪比为−5 dB时仿真如图3所示。
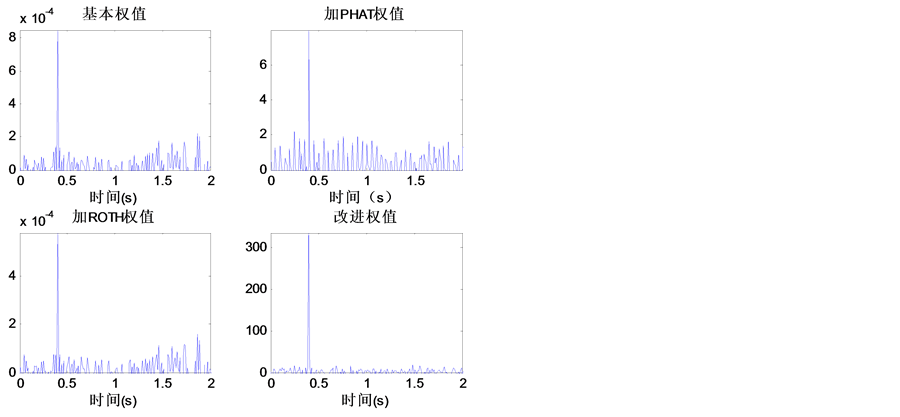
Figure 2. SNR 0 dB different weights
图2. 信噪比为0 dB各种加权
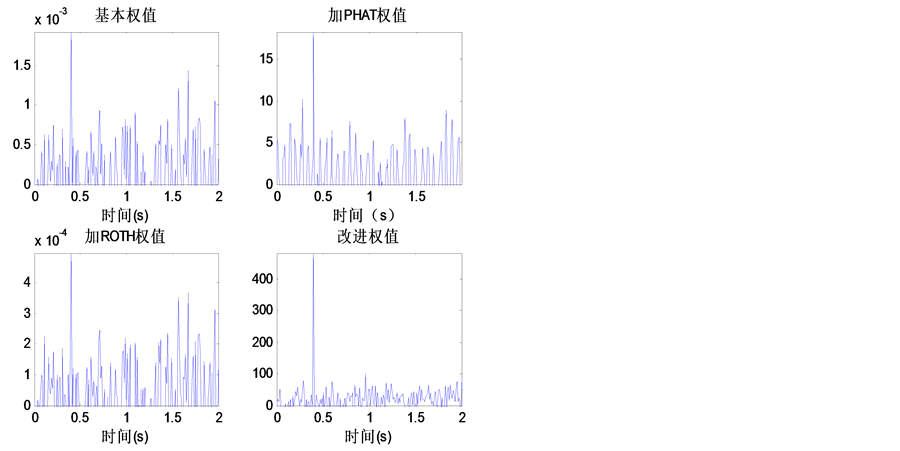
Figure 3. SNR −5 dB different weights
图3. 信噪比为−5 dB时各种加权
如图3中所示，在−5 dB时，各个权值都会出现噪声影响，但是互相关产生的波峰还尚未被淹没，基本权值和ROTH权值已经出现了次高峰，PHAT权值和改进的权值还能够出现较好的峰值。
在信噪比为−10 dB时仿真如图4所示。
如图4中所示，在信噪比为−10 dB时，基本权值和ROTH产生了严重的偏移，PHAT加权恢复出的信号已经被完全淹没，只有改进后的互相关函数的峰值仍比较尖锐。
4.2. 小功率信号仿真
小功率信号中采用
，选择的Fs的大小为200。
当信噪比为0 dB时如图5所示。
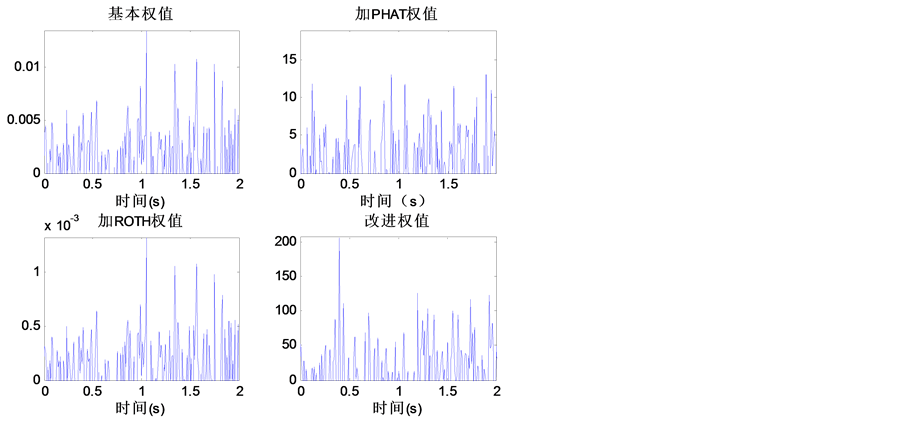
Figure 4. SNR −10 dB different weights
图4. 信噪比为−10 dB时各种加权
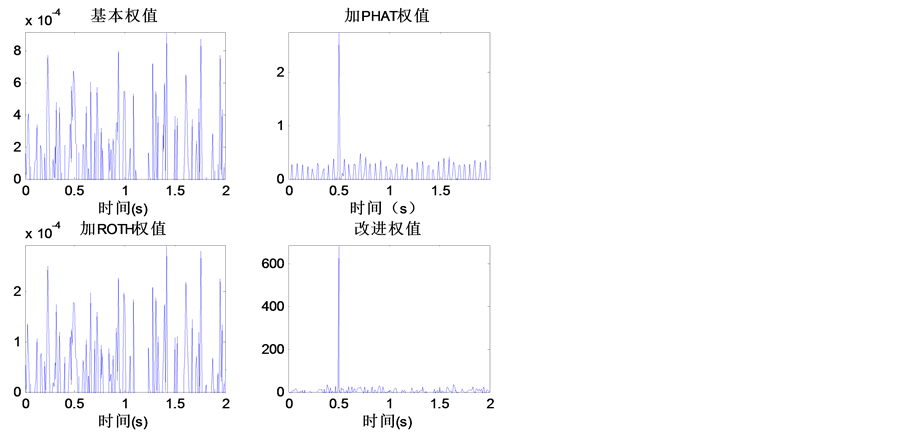
Figure 5. Small power signal SNR 0 dB different weights
图5. 小功率信号信噪比为0 dB各种加权
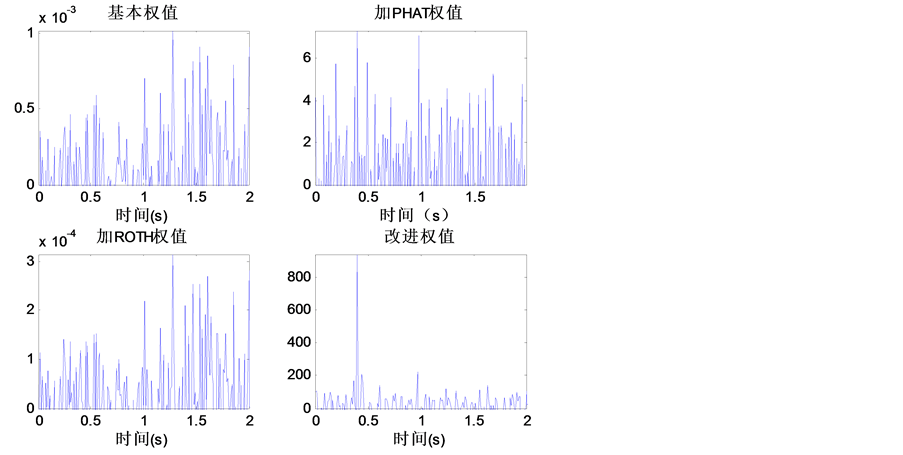
Figure 6. Small power signal SNR −5 dB different weights
图6. 小功率信号信噪比为−5 dB时各种加权
如图5中所示，信号功率较小时在信噪比为0 dB时，基本权值和ROTH权值已经被淹没，PHAT加权和改进的权值加权的互相关函数的峰值仍然能够比较尖锐，由于信号功率较小信号的波动较小，导致峰值检测比较困难，所以通过基本权值和ROTH权值检测峰值出现了峰值淹没。
当信噪比为−5 dB时如图6所示。
小功率信号时信噪比为−5 dB时基本权值和ROTH加权出现了严重的偏移，PHAT加权已经被淹没出现了多个峰值。而改进的权值峰值还是可以凸显出来，能够更好的估计出时延。
实际的小功率信号有较小的信噪比，用传统的加权方式很难得较好的峰值，导致时延估计得到的数据有误差，特别是在无线定位中，电磁波信号传播速度太快，很小的时延误差将会在实际定位距离中产生较大偏差，本文提出的新的加权估计能够较好的使用在无线定位中。
5. 总结
本文通过改进的权值在不同的环境中重新加权仿真，对比不同的权值计算，在信噪比为0 dB的环境中，常规的加权方法和改进的加权方法都能够精确估计，随着信噪比的变化，常规使用的权值将会出现峰值的偏移和多个峰值的现象，而改进的权值仍然能够精确估计。在实际环境中存在各种噪声并且信噪比要远远小于0 dB，本文通过理论推导和大量的试验仿真得到的新的权值能够在实际应用中简单方便的使用。