摘要:
考虑到直接用定义计算多维超几何分布高阶混合矩的复杂性,利用多维超几何分布的边际分布与联合分布的关系,给出了多维超几何分布高阶混合矩的简单算法及递推公式。
Abstract: Considering the complexity of computing the multidimensional hyper geometric distribution of high order mixed moments with definition directly, we use the relationship between marginal distribution and joint distribution in multidimensional marginal distribution, to give the simple algorithm and recursive formulas for multi-dimensional hypergeometric distribution of high order mixed moment.
1. 引言
在抽样调查中,我们经常遇到定性资料问题,为此有人曾探讨过“多维超几何分布协方差阵的简单求法[2] ”,下面我们就以抽样调查为背景来研究如何计算多维超几何分布高阶混合矩。假设总体含有 个个体,其中一等品有
个个体,其中一等品有 个,二等品有
个,二等品有 个,……,
个,……, 等品有
等品有 个。从总体中不放回地抽取容量为
个。从总体中不放回地抽取容量为 的样本,其中获得一等品
的样本,其中获得一等品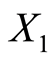 个,二等品
个,二等品 个,……,
个,……, 等品
等品 个。那么,
个。那么, 服从多维超几何分布,记为
服从多维超几何分布,记为
 ,即有,
,即有,

其中 ,
, 。
。
2. 预备知识
引理1[3] 设 服从超几何分布,记为
服从超几何分布,记为 ,则
,则
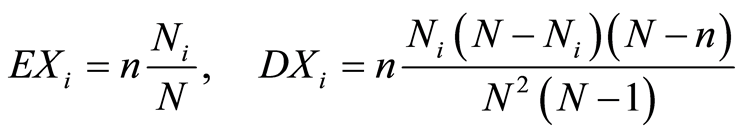
引理2[4] 设离散型随机变量 服从超几何分布,记为
服从超几何分布,记为 ,则
,则 的
的 阶原点矩可由公式
阶原点矩可由公式
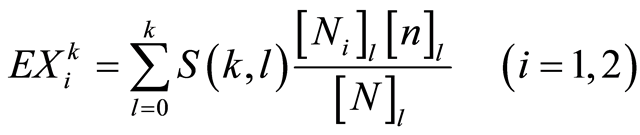
计算得出。
其中 为组合数学中的第二类Stirling数[5] ,其初始值为:
为组合数学中的第二类Stirling数[5] ,其初始值为:
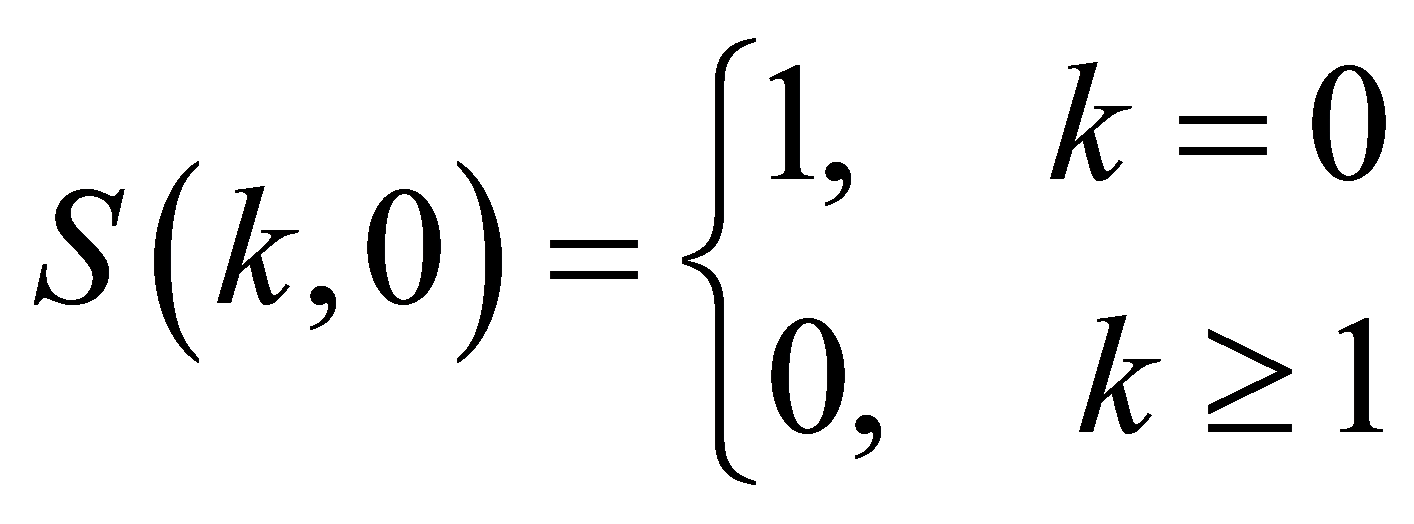
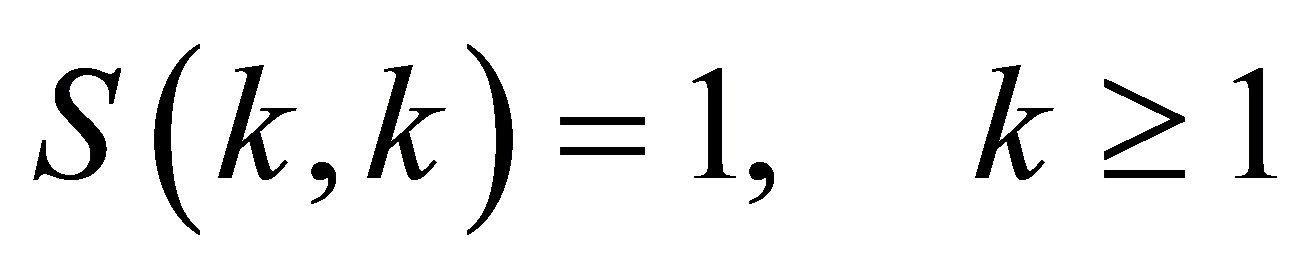
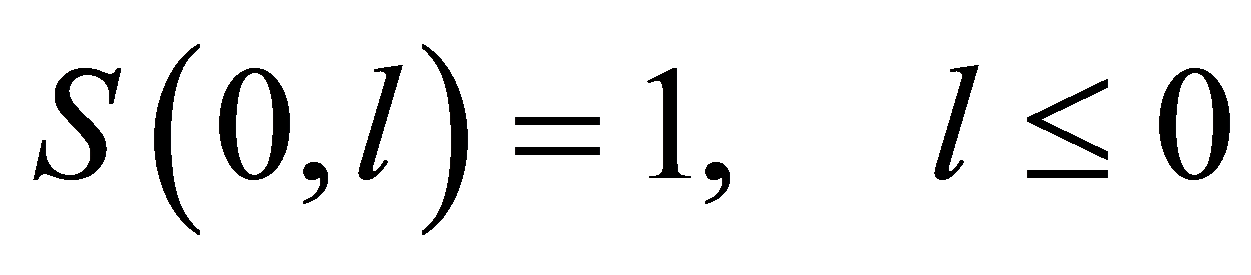
 为
为 的下阶层,并且
的下阶层,并且
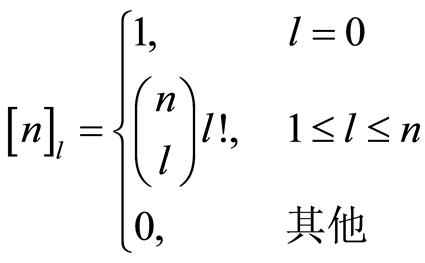
引理3 设离散型随机变量 服从多维超几何分布,记为
服从多维超几何分布,记为 ,为求
,为求 的
的 阶原点矩,可将其视为两类
阶原点矩,可将其视为两类 与
与
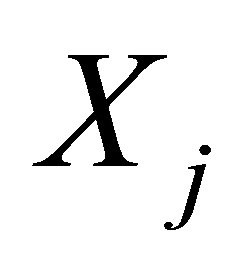 ,则根据引理2所述,
,则根据引理2所述, 的
的 阶原点矩仍可由公式
阶原点矩仍可由公式
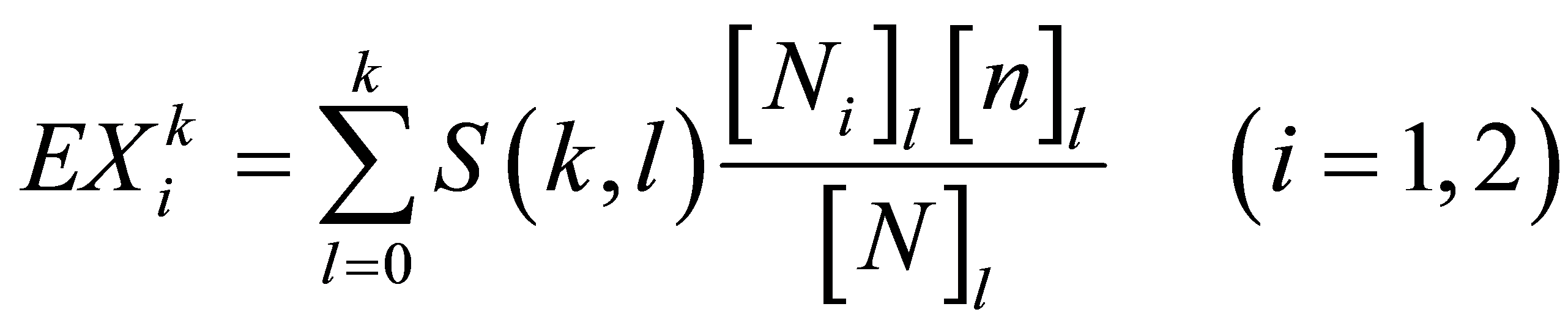
计算得出。
引理4[6] 设 服从多维超几何分布,
服从多维超几何分布, 是其中任意
是其中任意
 个分量,则
个分量,则 仍然服从超几何分布。
仍然服从超几何分布。
3. 高阶混合矩的算法
 时,
时, ,即等价为一维超几何分布,由引理2知
,即等价为一维超几何分布,由引理2知
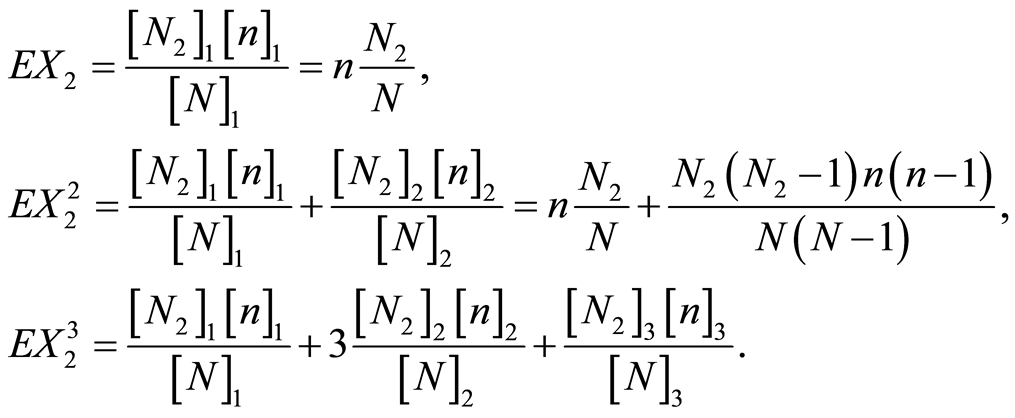
从而
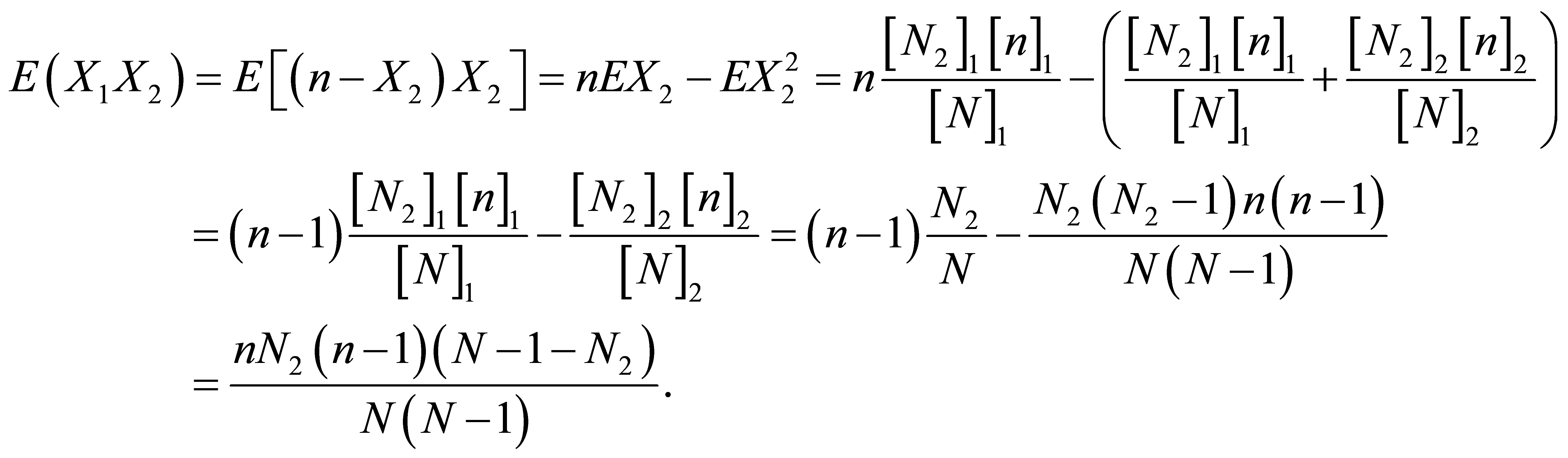
记为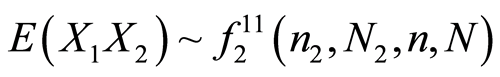
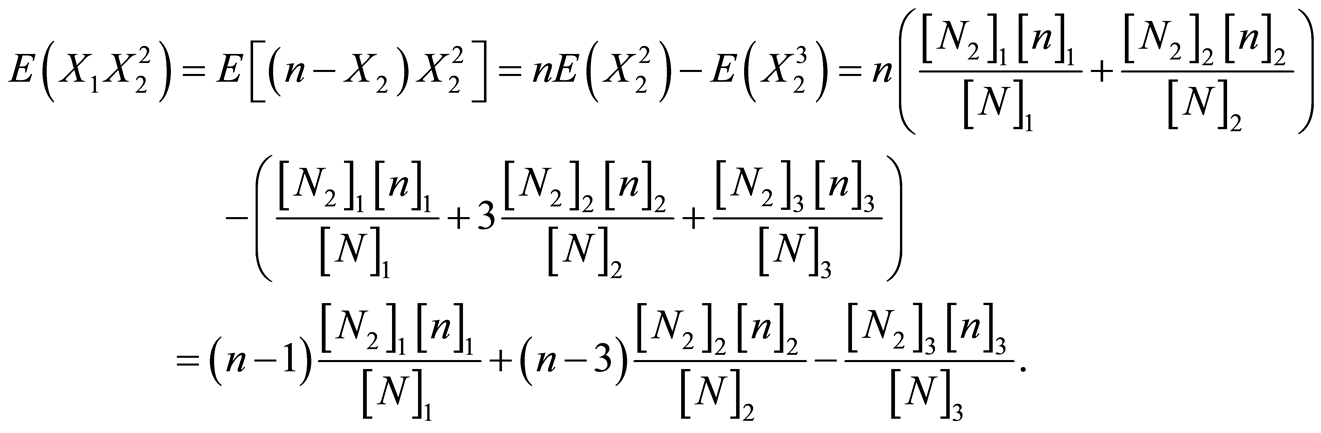
记为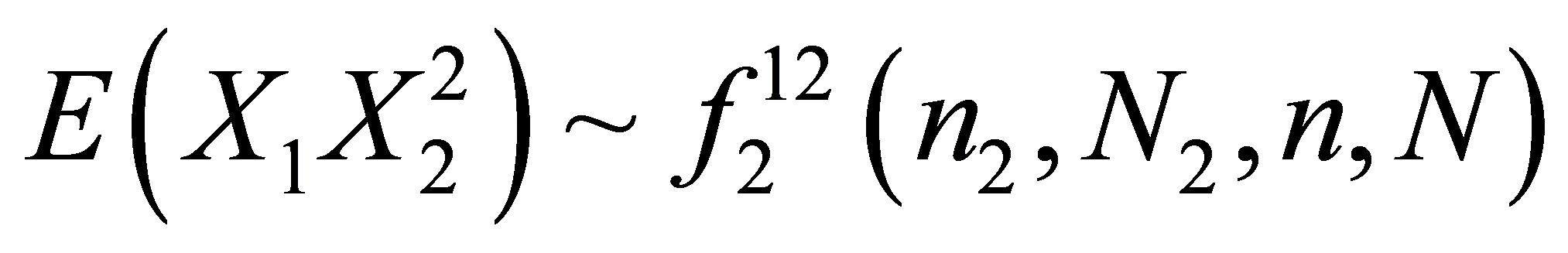
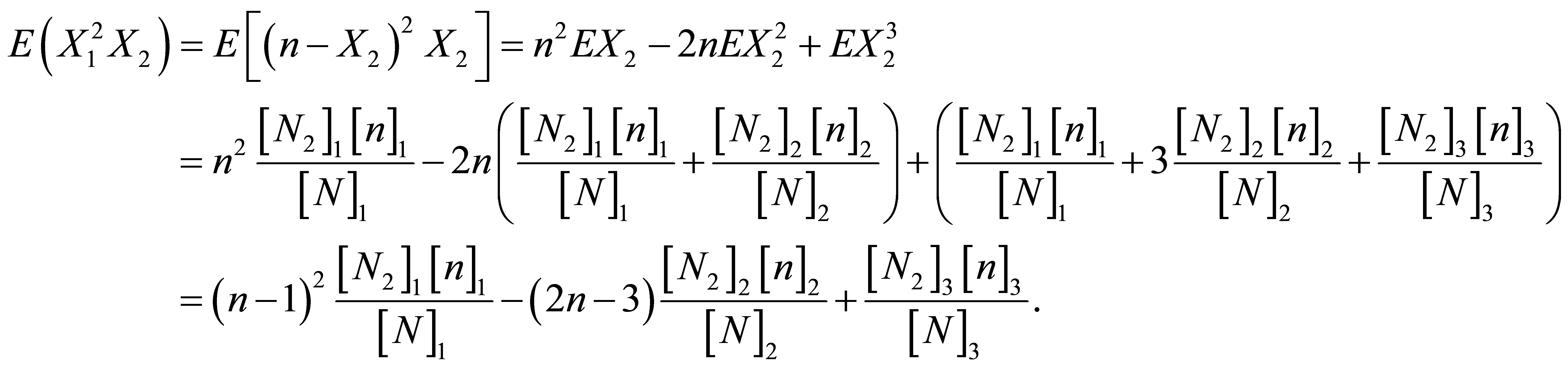
记为 。
。
推广到 时超几何分布任意高阶混合矩:
时超几何分布任意高阶混合矩:

记为 。
。
 时,
时, ,同样地我们有,
,同样地我们有,
 (*)
(*)
由引理3我们知道,
 ①
①
 ②
②
 ③
③
从而将①②③式代入到(*)式中得:
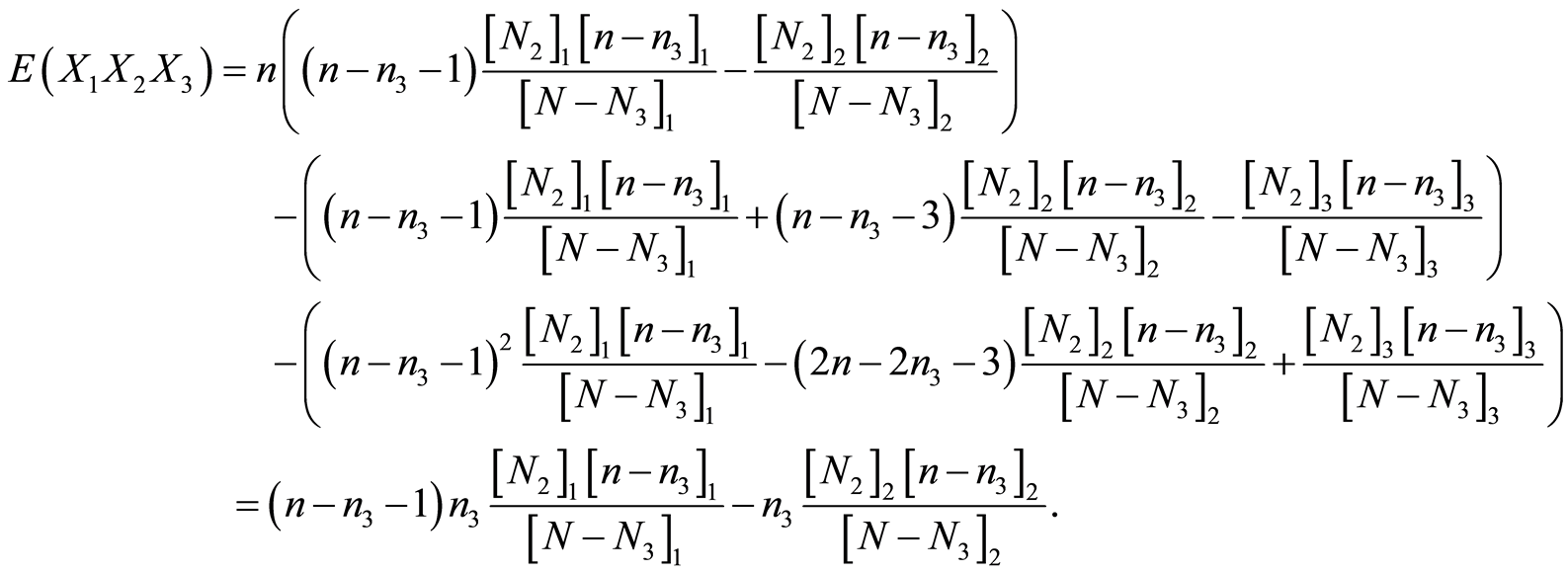
记为 。
。
同理,我们将之推广到 时超几何分布任意高阶混合矩:
时超几何分布任意高阶混合矩:
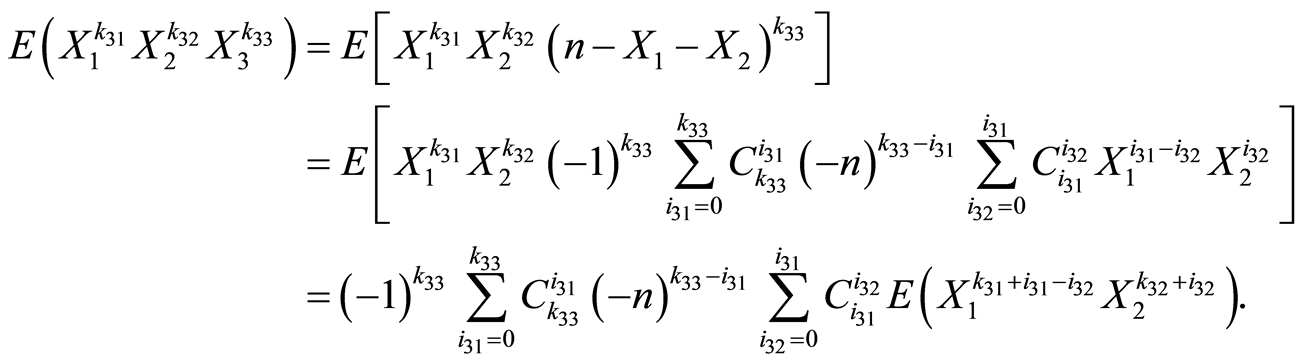
同样,由引理3我们知道
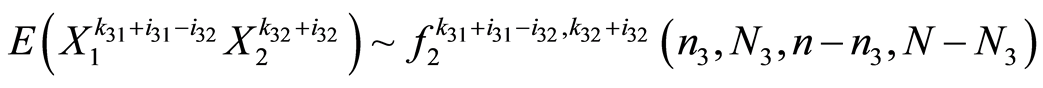
 时,任意高阶混合矩为:
时,任意高阶混合矩为:
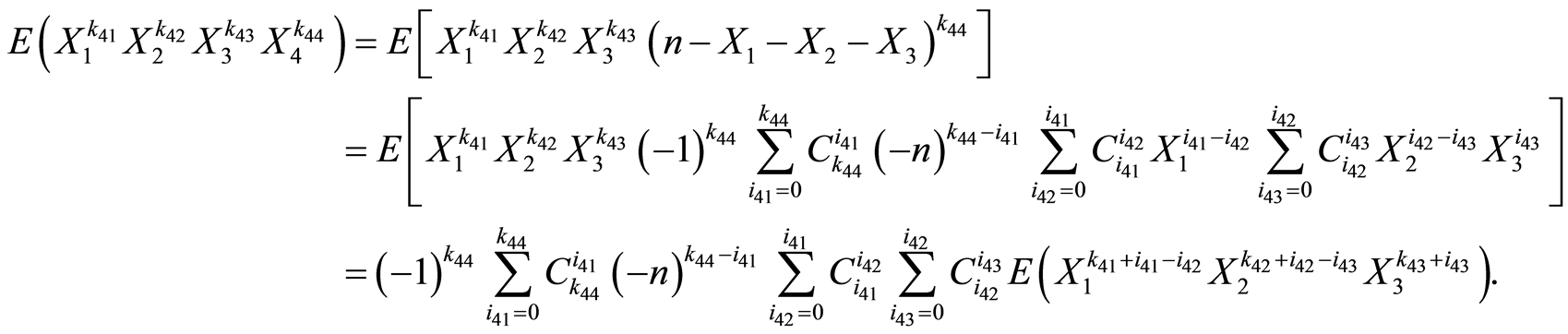
其中
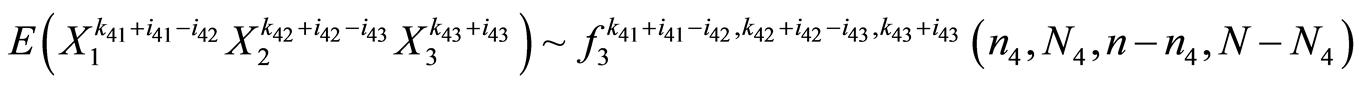
以此类推,可以得到:当求 维超几何分布任意高阶混合矩时,需要化成求
维超几何分布任意高阶混合矩时,需要化成求 维任意高阶混合矩来计算,即有如下形式的递推公式:
维任意高阶混合矩来计算,即有如下形式的递推公式:
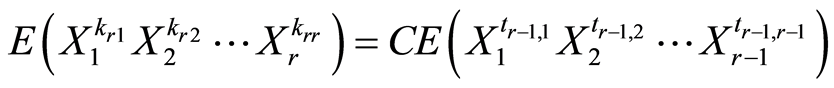
其中 为常数系数。
为常数系数。
从上面的计算中我们可以得知,变化后随机变量 的幂指数有如下规律,如表1:
的幂指数有如下规律,如表1:
系数 据有如下规律,如表2:
据有如下规律,如表2:

Table 1. Variation rule of order of each random variable in the mixed moment
表1. 混合矩 中各随机变量的阶数
中各随机变量的阶数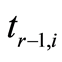 的变化规律
的变化规律

Table 2. Variation coefficient of C
表2. 系数 的变化规律
的变化规律
对于公式中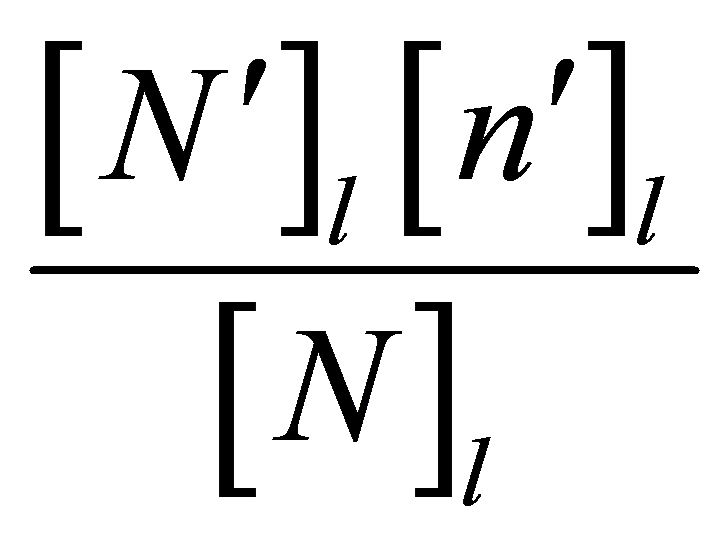 部分有如下规律:
部分有如下规律:
 时,
时, ,
,
其中 。
。
综上所述,我们得到计算多维超几何分布高阶混合矩的递推公式如下:
 ,
,
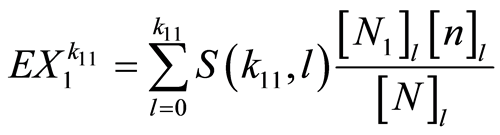
 ,
,
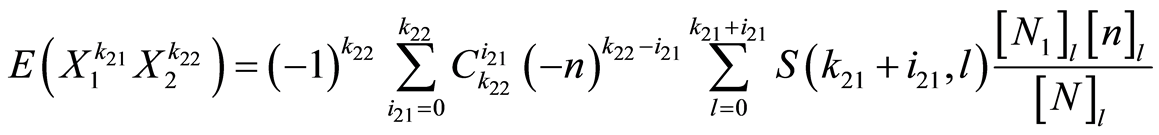
 ,
,
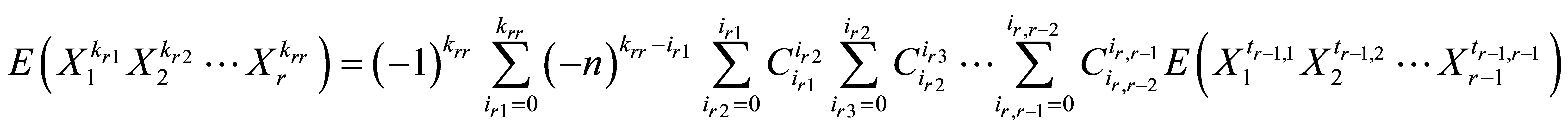
将其记为 式。其中
式。其中
 。
。
下面用数学归纳法证明上式成立:
 时,假设
时,假设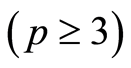
 时
时 式成立,即有:
式成立,即有:
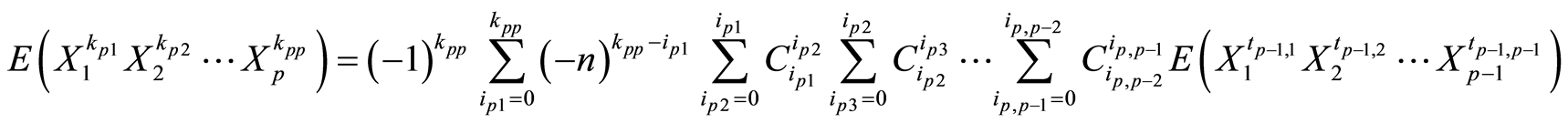
其中 。
。
则 时,
时,

这样一直把括号中的项拆分下去,并且根据假设,我们可以知道:
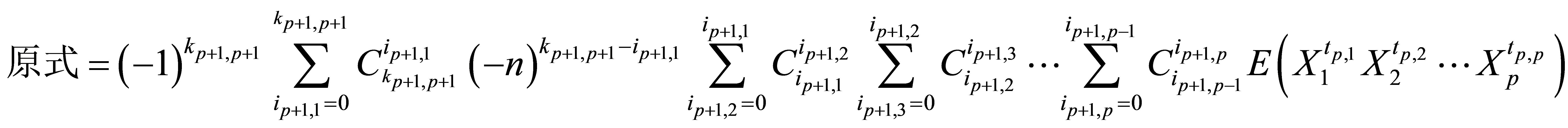
其中
 。
。
从而 式得证。
式得证。
基金项目
本文得到国家大学生创新训练项目(No. 201311413053)资助以及中央高校基本科研业务费(2009QS02)的资助。