1. 引言
推荐系统通过提供用户感兴趣的信息内容，在很多的网络应用 (比如亚马逊，淘宝网，Linked， Facebook等)中，已经成为了一个很有前途的处理信息过载的工具。目前，大多数推荐系统采用协同过滤技术(CF)，它通过挖掘相似用户或项目的历史行为数据来预测用户对某一项目的偏好。尽管协同过滤推荐算法已经成为推荐系统领域最成功的算法之一，但传统的协同过滤技术只利用了“用户–项目”二元关系而未考虑其它信息。当信息规模越来越大时，它的性能就遇到了很大挑战，比如数据的稀疏性(即缺乏足够数量的相似用户或项目)，由数据稀疏性及信息源的同质化则造成了推荐质量下降。
为了解决传统推荐算法遇到的问题，近期，有两种趋势在推荐系统研究领域吸引了大量关注：1) 上下文信息(比如时间，地点，用户情绪和天气等)已经成为影响推荐准确性的重要因素。比如用户可能会跟哥哥去看动作电影，但如果是跟女朋友一起的话可能更倾向于浪漫的爱情电影。在这种情况下，同伴对于电影推荐是关键的上下文信息。一些上下文感知推荐算法[1] 已经提出把上下文信息引入现有的推荐模型中，比如矩阵分解模型[2] 。2) 在线社交网络的发展带来了另一个所谓社交推荐的趋势。它依据用户社交网络中好友的兴趣来预测用户的偏好[3] 。理论上，社交推荐有助于缓解数据稀疏性(比如用户对于未评分项目的偏好可以根据他的好友的评分来预测)进而提高推荐质量(即用户跟好友通常有着相似的偏好)。
然而，现有的上下文感知推荐系统要么不能有效的联系不同种类的上下文信息，要么有着很高的计算复杂度(比如在超大数据集上应用矩阵分解模型)。现有的基于社交网络的推荐系统还不能系统的整合丰富多样的上下文信息进而做出准确的推荐。因此，本文考虑将社交网络信息和多维度的上下文信息整合进推荐系统中以进一步提高推荐质量。
本文提出一种整合社交网络信息的上下文感知推荐算法。主要内容包括：1) 首先提取多种可能会影响用户偏好的上下文信息。然后依据上下文信息利用随机决策树算法分割已有的用户项目评分矩阵(见图1(a))。经过分割所形成的子矩阵因为包含类似的上下文信息，因而彼此之间的联系更为密切，从子矩阵中预测评分比直接从初始矩阵中预测准确率更高。2) 在经过随机决策树分割产生的子矩阵上应用矩阵分解，以此预测潜在用户对项目的偏好。在矩阵分解模型的基础上，考虑到社交网络中好友对用户偏好的影响，通过用户对项目的已有评分来挑选那些和用户有着类似偏好的好友，利用基于上下文的皮尔森相关系数(PCC)来度量用户间的相似度，并引入了一个社交正则化项来提高推荐质量。3) 通过真实数据集上的实验结果表明，从均方根误差(RMSE)的角度来看，本文算法的性能要优于基本的社交推荐模型和上下文感知推荐系统。
(a) 
(b) 
(c)
Figure 1. Context-aware recommendation; (a) User-item-rating matrix; (b) Context-aware user-item-rating matrix; (c) Social network
图1. 上下文感知社交推荐；(a) 用户项目评分矩阵；(b) 引入上下文信息的用户项目评分矩阵；(c) 社交网络
2. 相关工作
2.1. 矩阵分解
利用矩阵分解方法(如SVD方法)可以将一个矩阵分解为两个(或多个)低维矩阵实现矩阵降维。同时，通过将分解得到的子矩阵相乘可以获得近似初始矩阵，并得到初始稀疏矩阵的某些近似值。具体到推荐问题中，一个矩阵分解模型能将一个用户项目评分矩阵
(m是用户数量，n是项目数量)分解为一个用户特征矩阵
和一个项目特征矩阵
：
(1)
其中
是能体现用户特征或项目特征的隐语义向量的维度，U的每一行为用户u的特征向量，V的每一列为项目v的特征向量。因此，
表示用户u对项目v的偏好，即考虑所有隐语义的兴趣度。
为了最大程度的近似初始矩阵R，即最小化预测评分和真实评分间的误差，同时考虑到用户项目评分矩阵的稀疏性，相应的目标函数定义为：
(2)
若用户i对项目j进行过评分则
为1，否则为0。为了避免模型过度拟合训练数据集，在(2)中加入了一个正则化项变为：
(3)
为Frobenius范数(A为一个X × Y的矩阵)，通过
来计算，参数
起着平衡训练误差和正则化项的作用，
越大，则模型预防过度拟合的能力越强，即泛化能力(预测新样本的能力)越强。
(3) 式可应用随机梯度下降法(SGD)来求解，通过迭代更新用户特征矩阵和项目特征矩阵[4] 。
2.2. 上下文感知推荐系统
上下文信息已被证明对于包括推荐系统在内的诸多应用领域中能提高预测的准确度[5] [6] 。它可以通过多个途径获取，比如直接从相关用户或项目处获取相关上下文信息，从数据或环境中间接取得，或者通过统计分析，数据挖掘，机器学习等技术来推测[7] 。近期的研究关注于建立一个能整合上下文信息和传统的用户项目评分信息的模型。例如，Karatzoglou等人通过对用户、项目、上下文的3维张量数据建模构建了一个多维推荐模型。但是，这个模型只适用于单一种类的上下文信息。尽管已经有了一些改进的方法使该模型适用于多种类型的上下文，然而，当初始用户项目评分矩阵很庞大时，这个模型仍然有着很高的计算复杂度。一种解决的方法是在应用任何分解模型之前分割初始矩阵。
2.3. 社交推荐
然而，现有的社交推荐模型在度量用户相似度时大都忽略了上下文信息。比如，即使用户和他的朋友有着相似的偏好，他对于一部电影的评分也可能在很大程度上被其它因素所影响，比如，用户的心情或者谁和他一起看的电影。近期的研究在处理社交网络信息时已经开始关注上下文。例如，有学者提出对有着相似偏好的用户以及他们选择的项目进行聚类。然后应用协同过滤技术通过子类信息(一种上下文信息)来提高top-N推荐质量。然而，这些研究都只考虑了非常基本的上下文信息(即聚类或分组信息)。也有学者[8] 提出将社交上下文(个人偏好和人际关系的影响)引入矩阵分解模型。然而，这些上下文信息仅仅和社交关系相关，没有考虑非社交上下文。相比之下，通过应用机器学习技术和矩阵分解，本文提出的SCRA可以不受信息类型限制，从两方面整合了一系列的上下文信息：1) 上下文直接用来分割初始评分矩阵；2) 应用基于上下文的皮尔森相关系数来提高用户相似性度量的准确性。
3. 基于社交网络的上下文感知推荐算法
3.1. 基本概念
在很多现实应用中都有着丰富的上下文信息，可以为推荐提供一个新的信息维度(见图1(b))。我们将上下文信息归为两类：1) 静态上下文，它描述了用户的特性，比如年龄，性别，人际关系，职业等，或者对于项目来说有种类，价格，物理特性等；2) 动态上下文，它反映了和评分有关的瞬时信息(比如，用户对项目评分时的心情或所处的位置信息)。另一方面，在线社交网络带来了另一种信息资源，通过这些信息我们可以从和用户具有相似偏好的朋友中推断用户对项目的偏好(见图1(c))。因此，在本文中，将上下文信息和社交网络信息引入矩阵分解模型中以进一步提高推荐质量。
用
来表示用户集，用
来表示项目集。任一用户可以根据自己的偏好对任一项目评分。假设评分值是一个在
中取值的离散值。很多推荐系统，比如MovieLens，采用五等李克特量表(Likert scale)(比如，[1,2,3,4,5])。用户
对项目
的评分用
来表示，所有的评分
组成了用户项目评分矩阵(见图1(a))。如前文所述，同样假设和每个评分相关联的上下文信息集合表示为
。这里每个评分都有相应的上下文信息向量并且对于各个种类的上下文信息的值域没有限制，即离散值和连续值都能接受。考虑到社交网络信息，定义了一个有向图
，边集E代表用户(U)间的关系。我们定义用户
的好友集为
。
3.2. 上下文感知推荐
为了有效结合不同类型的上下文信息，应用随机决策树算法，它是随机构造决策树的最精确的学习算法之一[9] 。算法能够依据不同类别的上下文信息依次分割初始评分集合R(即，用户项目评分矩阵)，这样一来就能将有着相似上下文的评分归为一簇。由于同一簇中的评分有着相似的上下文信息，从上下文角度来说，这些评分比初始矩阵中的评分有着更高的相关性，彼此之间有着更强的语义关联，因此，通过这些评分生成的预测评分也更为准确。
3.2.1. 随机决策树的构造
在一个特定应用场景中，有很多可利用的上下文信息，其中一些是和用户项目评分矩阵密切相关的，而其它的却不是这样。因此，在分割评分矩阵之前选择最相关的上下文信息是很重要的。机器学习，数据挖掘和各种统计方法[10] 可应用于预处理各种上下文信息。
经过预处理的上下文信息构成了上下文信息集合C。当构建决策树时，在树的每一层，我们从集合C中随机选择一种上下文信息
，根据
的值来分割评分矩阵(见图2)。举例来说，若上下文信息
为时间上下文，则可以根据时间段来分割评分矩阵(即，从星期日到星期六的每一天)。一旦在树的一层上评分分割完成，则随机选择的
就会从上下文信息集中被删除：
，这样一种上下文信息在一棵树中只处理一次。
分割的过程一直持续到满足下列要求之一：1) 处理完所有的上下文信息；2) 树的层次已经达到限定值；3) 在当前结点处没有足够数量的评分去分割。分割完成后，评分R基于不同的上下文信息被分类。
3.2.2. 用户评分预测
鉴于上下文信息是在树的每一层随机选择的，因此在不同的决策树中，训练评分的分类也是不同的。假设预测评分为
，设有T棵决策树，在每棵决策树中，根据
的上下文信息将它分类到评分子集(即用户项目评分子矩阵)
中。将各个
(如图2中的
)进行矩阵分解，并依据下面的目标函数得到用户特征矩阵
和项目特征矩阵
：
(4)
将上式求得的用户特征矩阵
和项目特征矩阵
相乘得到预测评分：
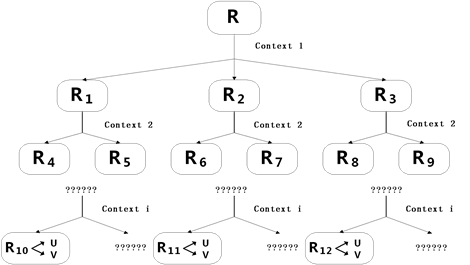
Figure 2. Random decision trees (one tree)
图2. 随机决策树(单个树)
(5)
最后，结合T棵决策树的预测生成最终的预测评分：
(6)
通过结合不同决策树的多个预测，考虑所有的上下文信息，生成个性化和比较精确的上下文感知推荐。此外，通过去除不相关(从上下文角度)的评分，产生的子矩阵明显小于庞大的初始评分矩阵，从而大大的降低了计算复杂度。
3.3. 基于社交网络的改进算法
3.3.1. 用户相似度计算
虽然朋友的意见有利于给用户提供高质量的推荐，但大多数现有的研究要么没有细粒度的信息过滤而利用所有可得的社交网络信息，要么没有深入探讨如何精确度量两个用户之间的偏好相似度。为了解决这些问题，引入了一个社交正则化项。在现实世界中，用户可能有成百上千个朋友，有的朋友可能和用户有着非常相似的偏好，有的却有着完全不同的偏好。因此，在计算偏好相似度时对所有朋友同等看待是没有意义的。为了解决社交偏好的多样性，考虑到用户和他每个朋友之间偏好的相似度引入正则化项：
(7)
其中
是控制社交正则化项大小的常量，
表示用户
和他的好友
基于历史评分的偏好相似度。高的相似度得分意味着基于过去已评分的项目，
和
有着很相似的偏好，低得分则表示
和
的偏好很不一样。
从公式7中我们可以看到，一种整合社交网络信息的方法是计算用户和每个好友之间的相似度，这可以根据他们的历史评分信息来度量(即用户和好友都进行过评分的项目信息)。在现有的相似度计算方法中，皮尔森相关系数(PCC) [11] 已被证明在很多情况下比其它方法(比如向量空间相似度)更加准确。因此，在本文中，应用PCC计算用户
和他的好友
之间的相似度：
(8)
其中，
表示用户
和
都评分过的项目集，
和
分别表示用户
和
的平均评分。
3.3.2. 基于上下文的用户相似度计算
PCC的一个优点是它考虑到有些用户会对大部分项目给予很高的评分(例如，在五等Likert scale中的4或5)，而另一些挑剔的用户通常会给予低评分(例如，在五等Likert scale中的2或3)。然而，这个经典的相似性度量方法只利用了评分的值，未考虑任何上下文信息，而上下文是另一类对相似度计算很有价值的信息。为了进一步提高用户相似度计算的精度，提出了一种融入上下文信息的皮尔森相关系数：
(9)
c代表上下文信息，项目
的权重
通过下式计算：
(10)
其中归一化函数
限定给定的值范围在[0,1]内，
表示用户
对项目
的评分
和用户
对项目
的评分
之间的皮尔森相关系数。注意这里的PCC通过和每个评分有关的上下文信息向量来度量:
(11)
这里，
表示用户
对项目
的评分
所对应的上下文向量实例，
表示用户
对项目
的评分
对应的上下文向量实例。
,
分别表示
,
的平均取值。
,
均取自3.1节中定义的上下文信息向量。显然，高权重
意味着用户和他的好友在相似的上下文中做出了同样的评分，因而对整体的相似度有着更大的影响。
3.3.3. 目标函数的生成
我们将基于上下文的相似度
的范围限定在[0,1]。之后再将它应用到推荐模型。利用公式8和10，公式4转化为：
(12)
上式可以应用梯度下降法来解，通过迭代更新求得
和
。
(13)
(14)
其中
为学习率，迭代次数对于算法性能的影响将会在实验结果评价部分加以讨论。
4. 实验结果及评价
4.1. 实验方法
4.1.1. 实验数据集
豆瓣是中国最大的书籍，电影和音乐的推荐和评论分享社交平台。每个用户都可以对书籍，电影和音乐做出评分(从一星到五星)，以表明他对该项目的偏好程度。每个评分都有一个对应的时间戳。若用户还未消费过对应项目，仍可以通过添加类似“wish”的标签表达他的兴趣。这里存在的社交网络使得用户可以追随那些发布有趣或有用评论的用户。表1展示了该数据集的统计资料。注意这里我们只选用显性的评分，即“wish”不做为评分。
我们选择豆瓣数据集是因为它不仅包含相关的时间信息等上下文信息，并且含有社交信息，因此它很适合用来测试本文提出的基于社交网络的上下文感知推荐算法。随机选取80%的评分来训练推荐模型并利用余下的20%评分来测试算法的性能。
4.1.2. 实验对比
据我们所知，现有的推荐系统还不能系统结合上下文信息和社交网络信息来给出高质量的推荐。在本节中，将对SCRA和现有的上下文感知推荐算法，社交推荐算法，基于用户或项目的协同过滤算法进行比较。
RPMF是随机分割矩阵分解的简称，是一种利用随机分割技术基于树结构构造的上下文协同过滤模型。具体来说，它将具有相似上下文的评分分配到决策树的同一结点上。然后，在每个结点上应用矩阵分解来预测评分。多个结点和决策树上的预测结合起来生成最终的推荐。尽管该模型所提出的算法也用到了基于树的方法，但和本文提出的算法相比，它们仍有着明显的不同：1) RPMF通过处理和上下文信息相关的隐语义的值间接处理上下文信息，而本文提出的SCRA直接处理上下文信息；2) RPMF在树的每个结点都应用矩阵分解，而本文提出的SCRA仅在树的叶子结点应用矩阵分解。另一个重要的不同之处在于RPMF未考虑任何的社交网络信息。
SoReg是一种基于社交网络信息的推荐模型。在基础的矩阵分解模型的基础上加入了一个社交正则化项。它有两种变式：1) 基于平均值的正则化，它限制用户的偏好值和用户好友偏好平均值之间的差异；2) 基于个体的正则化则限制用户偏好和他每位好友的偏好之间的差异。实验中，我们只比较本文的算法和更为精确的基于个体的变式。
基于项目的协同过滤算法首先找到潜在用户评分过的并且和待预测项目最为相似的项目集，然后通过求这些近似项目评分的加权平均值来预测评分值。
基于用户的协同过滤算法结合了一组和潜在用户有着相似评分模式的最近邻用户的评分来预测评分。
基于数据集中可以取得的信息，对于包含有上下文信息的推荐算法，提取出5类上下文信息：1) 一天中的每小时，即用户在几点做出的评分；2) 一周中的每一天，即用户在星期几做出的评分；3) 用户评分时目标项目中“wish”的数量(仅对豆瓣数据有效)；4) 潜在用户的平均评分值；5) 目标项目的分类。
4.1.3. 评价指标
我们使用均方根误差(RMSE)来度量和比较多种推荐算法的性能，它由下式定义：
Table 1. Statistics of the Douban dataset
表1. 豆瓣数据集统计资料
(15)
其中N为预测总数，
是对项目的真实评分，
是相应的预测评分。每个实验重复十次。由于所有实验中的方差都很低(即95%置信区间)，为了避免混乱，没有设定误差标准线。测试采用双尾检验配合t检验(p值<0.001)，所有相关测试结果都有着明显的统计意义。
4.2. 结果评价
首先用豆瓣数据集来讨论SCRA中多个参数对算法性能的影响。经过交叉验证，我们设定正则化常量
。图3显示当应用数据集的不同子集(即，书集，电影集和音乐集)时，参数
的变化对算法性能的影响，其中
控制着有多少社交网络信息被整合进算法中。本实验中，设定隐语义向量维度和求解一个矩阵分解模型的迭代次数分别为10和20。随后将介绍这两个参数是如何影响不同基于矩阵分解的推荐模型性能的。注意到当
增大，RMSE首先变小，当
到达某一个临界值时(约0.01)，RMSE便保持相对平稳(有微量增大)。由此得出结论，社交网络信息可以有效的改善推荐质量，并且
是个合适的临界值，这个临界值可以很好的平衡用户项目评分矩阵和社交网络信息。
另一个影响算法性能的是评分预测时所用的决策树的数量。图4表明少量的决策树(即2或3)就可以实现高质量的推荐。这个结果同样证明了算法的计算复杂度在应用中处在一个合理的范围内。在接下来的实验中，我们设定本算法的决策树数量为3。
接下来讨论上下文信息量的影响。首先控制决策树的高度为一确定值。如果设定树的高度为1，那么在每棵树中都只有一类的上下文信息被利用。如果设树高为4，则所有的上下文信息都被用于推荐。由图5可以看出，越多的上下文信息被利用，算法性能就越好(即更低的RMSE)。同样证明了，一方面，上下文信息可以极大的提高推荐质量，另一反面，所选择的上下文信息(见4.1.2节)是很有效的。
最后，利用豆瓣数据集对SCRA和其它的推荐算法进行对比。在这之前，需要首先确定两个重要的参数。即隐语义向量维度和基于矩阵分解模型的迭代次数。先把迭代次数定为10，然后观察RMSE在不同维度的隐语义向量下的变化(见图6)。发现RMSE随着隐语义向量维度的增加而减少，这就意味着，更大的维度会带来更高的准确度。然而，当维度增加到10(一些情况下甚至为8)左右，推荐质量的提高就变得微不足道。由此得出结论，对于基于矩阵分解的模型(在豆瓣数据集上)只要有少量的隐语义就足够了。
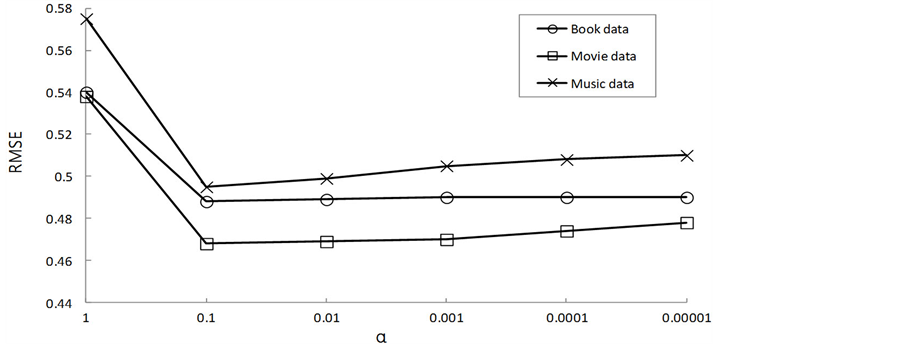
Figure 3. Impact of parameter α; Experimental parameters (λ = 0.1, α = 0.01, latent factor dimensionality = 10, iterations = 20)
图3. 参数α的影响；实验参数(λ = 0.1，α = 0.01，隐语义向量维度为10，迭代次数为20)
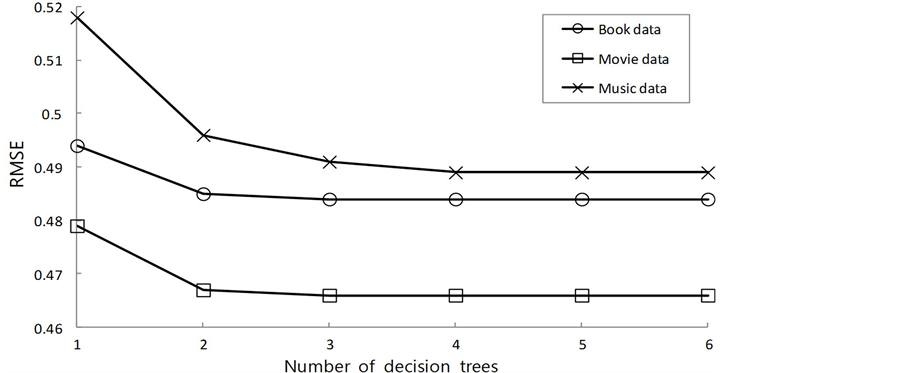
Figure 4. Impact of number of decision trees (λ = 0.1, α = 0.01, latent factor dimensionality = 10, iterations = 20)
图4. 决策树数量的影响(λ = 0.1，α = 0.01，隐语义向量维度为10，迭代次数为20)
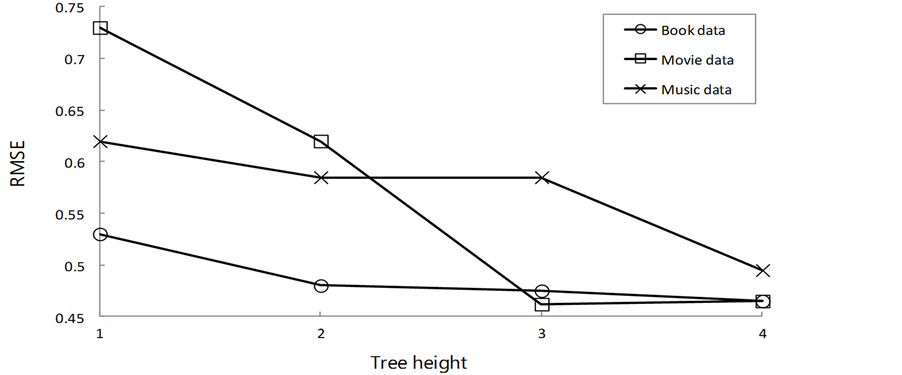
Figure 5. Impact of quantity of contextual information (λ = 0.1, α = 0.01, latent factor dimensionality = 10, iterations = 20)
图5. 上下文信息量的影响(λ = 0.1，α = 0.01，隐语义向量维度为10，迭代次数为20)
在下面的实验中，分别设定SCRA，SoReg和RPMF隐语义向量的维度为可以使RMSE趋于稳定且较低的临界值(即[8, 10])。类似的，如图7所示设定所有基于矩阵分解的模型迭代次数为一临界值(即[20, 30])，因为越高的迭代次数会带来更高的计算量，但却不能明显降低RMSE。
一旦参数确定下来，就可以分别用书籍数据，电影数据，音乐数据和完整豆瓣数据去测试不同推荐模型的性能(表2)。
总结了测试结果。注意到，在所有的实验场景中，SCRA都要比其它的推荐算法更精确。所有基于矩阵分解的模型都要明显胜过传统的基于项目和基于用户的协同过滤算法，这也证明了矩阵分解技术在推荐系统领域里的优势。实验结果同样说明，同时包含上下文信息和社交网络信息的推荐算法比那些只含有其中一种信息的推荐算法(即，SoReg和RPMF)具有更高的推荐质量。SoReg比RPMF性能稍好说明了处理过的社交网络信息对提高推荐系统的质量更有效(至少在豆瓣数据集上是这样)。总体来看，在完整的豆瓣数据集上，从RMSE角度，相应地提高了13%~25%。
Table 2. Performance comparison on the Douban dataset
表2. 豆瓣数据集上的性能对比
(a) SCRA 
(b) SoReg
(c) RPMF
Figure 6. Impact of latent factor dimensionality (iterations = 10)
图6. 隐语义向量维度的影响(迭代次数为10)
(a) SCRA 
(b) SoReg
(c) RPMF
Figure 7. Impact of iterations
图7. 迭代次数的影响
5. 结论
本文提出了一种基于社交网络的上下文感知推荐算法，它系统的结合了上下文信息和社交网络信息来提高推荐质量。该算法首先应用随机决策树算法基于各种上下文因素分割初始评分矩阵。所产生的子矩阵中的评分处于相似的上下文中，因而彼此之间相关度更高。再对子矩阵应用矩阵分解来预测评分。为了有效地整合社交网络信息，算法引入了一个社交正则化项，通过学习用户好友的偏好来预测用户的偏好。为了识别有着相似偏好的好友，提出一种融入上下文信息的皮尔森相关系数来度量用户相似度。在真实数据集上进行的实验表明，SCRA性能明显优于传统的上下文感知和社交推荐模型。
该领域有待进一步研究的问题是：针对不同的应用场景如何提取和聚类Web用户的上下文信息及相关的社交网络信息，使得SCRA算法为用户提供更加精准的Web内容推荐。
基金项目
本文受辽宁省自然科学基金(2014020068)资助。