1. 引言
雷达目标跟踪的过程是利用已获得的雷达观测数据，对目标当前空间位置进行估计或未来空间位置进行预测的过程。这一处理过程不可避免的需要对离散观测数据进行统计处理，良好的处理效果与目标运动模式的正确选择是密不可分的。关于目标运动模式通常是未知的，具有信息不对称性 [1] 。现有文献的处理方式主要有两种，一是基于目标的连续运动模式，这是忽略目标运动的状态噪声，或将状态噪声视为融入目标运动的状态改变因素中，直接基于观测数据进行估计与预测；二是在目标运动的状态中引入状态噪声，而量测噪声与状态噪声无关，基于状态方程与量测方程联合估计与预测目标的运动状态。无论采用何种处理方式，都回避不了目标运动方式或模式或运动特征的检测。本文基于目标连续运动的假设，在对测量数据进行无偏量测转换的基础上研究平面运动模式的参数估计与检测问题，并对检测方法进行了仿真验证。
2. 测量数据的无偏量测转换
设在以雷达观测点为坐标原点的局部坐标系下目标在某个时刻的真实位置的直角坐标为
，雷达测量对应的斜距为
，俯仰角为
，方位角为
，相应的真实值分别为
。记雷达的斜距、俯仰角与方位角的测量误差分别为
，则有
(1)
若进一步简单地假设
满足如下两个条件：
1)
相互独立，这一点与工程实践是相符的；
2)
均服从期望值为0的正态分布，其标准差分别为
，在工程实践中标准差用于表示雷达的测量精度，均为已知值。
根据测量值
，不难得到直角坐标下的间接测量值可取为
(2)
根据关于
的假设不难计算出间接测量值的期望值分别为
(3)
又根据概率论知识可得
， (4)
， (5)
从而可得
(6)
因此要使得通过测量数据转换得到的直角坐标的间接测量值为真实值的无偏估计，必须取直角坐标的测量值向量
为如下形式：
(7)
为了方便后续的统计检测问题的研究，将上式中的直角坐标测量值向量
的协方差矩阵
计算如下：
其中各元素取值为
，
，
说明一点，无偏量测转换只需利用已知数据进行处理即可，而转换后的数据的协方差矩阵的计算则需要用到量测的真实值，这是无法直接获得的。因此在后续的数据处理中用测量数据近似，即式中的
常用测量数据
近似或者说估计。
更为重要的是，在
的正态分布假设条件下，由于转换后的测量数据
的概率分布很难求得，因此，在本章的统计分析中，将
的联合分布近似为三维正态分布，这也是一种不得已而为之的近似。从这一角度来说，本文的平面运动检测方法只是一种近似方法。
3. 平面运动模式中的参数估计
机动目标的平面运动检测问题可描述如下：
设雷达测量得到的观测数据经无偏转换后为
，单组坐标数据
近似服从正态分布，已知其协方差矩阵为
，考虑显著性假设检验问题：
共面；
不共面
在这一问题的统计分析中，我们将其分解为线性回归模型中的两个子问题：
1) 寻找回归平面方程，即确定回归平面方程的系数；
2) 检验变量之间线性关系的显著性。
关于寻找回归平面方程问题，其具体描述如下：
将
中的两个固定的分量近似视为非随机变量即可控变量，剩余的变量视为观测变量，如将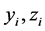
视为可控变量，
视为观测变量，则可近似得到回归模型如下
其中
为上一节中给出的协方差矩阵中对角线上的第一个元素。
采用线性回归理论的描述方式则为
其中，设计矩阵
，
待估参数
，
观测向量
，
，
为对角阵。
由于假设
已知，此处的回归模型又与常用的线性回归模型略有区别。
根据线性回归理论，可得待估参数
的广义最小二乘估计值为
(8)
从而得到回归平面方程，即对给出目标运动所在平面方程的估计式。
基于上述讨论，关于回归平面方程的确定其实还有一个将哪两个变量近似为可控变量的策略问题，这里显然有3种选择方式。本文采用的策略是3种选择方式全部考虑，从拟合的残差及统计显著性的最佳效果角度综合比较。
4. 平面运动模式的统计检测方法
在上一节中已经将目标的平面运动模式检测问题简化为线性回归效果的显著性检验问题，而这一问题在统计学中又分为对单个变量的显著性检验问题和整体回归效果检验问题 [2] 。这里从工程实践的角度，只关心整体回归效果检验问题。
在线性回归理论中，一个随机变量与多个随机变量之间的线性相关程度是一个复杂的问题，通常采用复相关系数进行判断，但复相关系数又不能完全解决这一问题。本文在本章第一节与第二节的假设与简化下，问题的解决过程可相应地得到极大程度的简化。
事实上，在第二节的假设条件下，若记
，
则有
，即回归方程的广义残差平方和
服从自由度为
的
分布。
因此关于目标的平面运动检测的统计量取为
(9)
若给定的显著性水平为
，则相应的检验临界值应取为
，即分布
的上
分位数。若
，则认为目标是非平面运动；否则，接受目标为平面运动的统计推断。
5. 检测方法的仿真验证与结论
仿真场景选择单个目标机动的场景，这里场景的部分参数设置参考了文献[3] 。
目标的初始位置为(70, 70, 20) km。第一阶段：初始速度为(100, 175, 10) m/s，匀速运动20 s；第二阶段：在与水平面垂直的平面内作匀速转动20 s，转速为0.5 rad/s；第三阶段：以加速度(70, 90, 10) m/s2机动10 s；第四阶段：匀速运动15 s；第五阶段：匀减速直线运动10 s，加速度大小为20 m/s2机动。
量测周期为0.5 s，雷达的测量精度为：斜距50 m，俯仰角与方位角均为0.8725 mrad。
利用MATLAB软件编程得到检测方法的仿真结果如下：
检测时间段：3个时间段，分别为[0, 40 s]，[0, 50 s]，[0, 75 s]
检测统计量的取值：分别为68.6127，202.8311，482.9736
临界值：分别为98.4844，120.9896，176.2938
结论：第一个时间段内目标做平面运动，另外两个时间段则不是，与仿真设定吻合。
*通讯作者。