1. 引言
微分算子的谱理论作为微分算子理论的基本问题之一,已经成为量子力学等领域的重要数学工具。关于带权函数的Sturm-Liouville边值问题,带有自伴边界条件的右定问题已经有非常完善的谱理论,而不定问题的谱结构与右定问题有很大区别。例如,不定Sturm-Liouville边值问题的实特征值上下无界,更关键的是会出现非实特征值。自1918年Richardson提出了关于Richardson方程非实特征值的存在性 [1] ,之后很多学者开始关注和研究带有不定权的Sturm-Liouville问题非实特征值的相关问题 [2] [3] [4] ,文献 [5] 给出了在分离边界条件下正则不定Sturm-Liouville边值问题非实特征值存在的充分条件,并得到了权函数仅变号一次和权函数可变号任意次时非实特征值的界。文献 [6] 给出了在绝对连续函数限制下正则不定Sturm-Liouville边值问题非实特征值的界。而对于四阶不定微分算子谱问题的研究则相对较少,文献 [7] 给出了四阶不定微分算子非实特征值的界。
本文考虑四阶不定微分方程
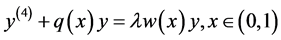 (1.1)
(1.1)
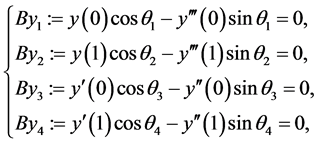 (1.2)
(1.2)
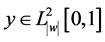 ,
, ,其中
,其中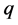 ,
,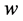 为实值函数,满足条件
为实值函数,满足条件
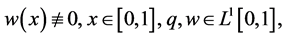 (1.3)
(1.3)
且权函数 在
在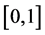 上变号,其中
上变号,其中 是谱参数。令
是谱参数。令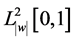 为具有内积
为具有内积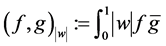 和范数
和范数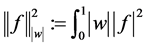 的Hilbert空间。
的Hilbert空间。
令
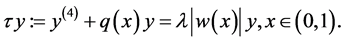 (1.4)
(1.4)
则(1.1),(1.2)相应的右定问题是(1.4),(1.2)。
本文将在文献 [5] 的基础上考虑四阶不定微分算子的相应情况,给出问题(1.1),(1.2)的权函数仅变号一次和权函数可变号任意次时非实特征值的估计。
2. 主要定理及其证明
命题2.1 [7] 如果问题(1.1) (1.2)有非实特征值,则问题(1.4) (1.2)至少有一个负特征值。
命题2.2 [7] 如果问题(1.4) (1.2)有n个负特征值,则问题(1.1) (1.2)至多有2n个非实特征值。
令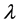 为问题(1.1) (1.2)的特征值,
为问题(1.1) (1.2)的特征值,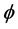 是相应的特征函数且
是相应的特征函数且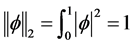 ,则
,则 满足方程(1.1)及边界条件(1.2)。即
满足方程(1.1)及边界条件(1.2)。即
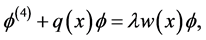 (2.1)
(2.1)
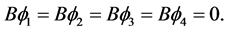 (2.2)
(2.2)
令
 . (2.3)
. (2.3)
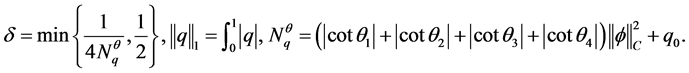 (2.4)
(2.4)
当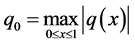 时。定义当
时。定义当 时,
时, ,由(2.4)易知
,由(2.4)易知 ,因为
,因为 ,所以可选
,所以可选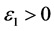 ,使得
,使得
 (2.5)
(2.5)
引理2.3 对如上的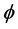 ,有
,有
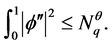 (2.6)
(2.6)
其中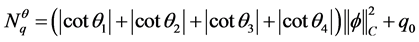 。
。
证明:在方程(2.1)的两边同时乘以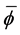 ,然后在
,然后在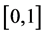 上进行积分,再由(2.2)可得
上进行积分,再由(2.2)可得
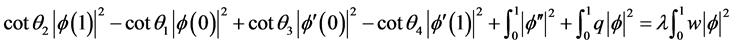
由 ,上述等式可推出
,上述等式可推出 ,因此
,因此
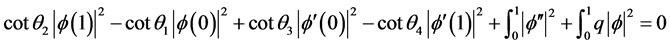 (2.7)
(2.7)
再由(2.3)和(2.7),可得
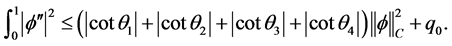
引理2.4 对如上的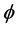 ,存在一个长度为
,存在一个长度为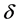 的区间
的区间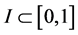 ,其中
,其中 ,
,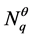 见(2.4),使得在
见(2.4),使得在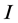 上
上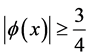 和
和 。
。
证明:对任意的长度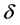 的区间
的区间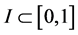 ,由Cauchy-Schwarz不等式和(2.6),得
,由Cauchy-Schwarz不等式和(2.6),得
 (2.8)
(2.8)
取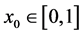 满足
满足 ,则对于
,则对于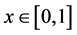 和
和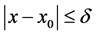 时,可得
时,可得

和
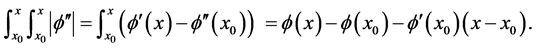
由(2.8)可得
 (2.9)
(2.9)
又由于对任意的 和
和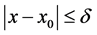 ,可得
,可得
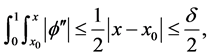
根据 的定义,在
的定义,在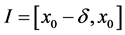 或
或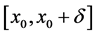 上成立
上成立 。
。
由Cauchy-Schwarz不等式和(2.7),得到

因此根据 的定义,在
的定义,在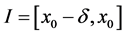 或
或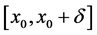 上成立
上成立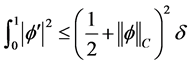 。
。
定理2.5 假设 ,
,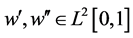 。当
。当 ,
,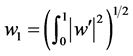 ,
,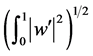 和
和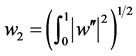 时,则对(1.1) (1.2)的任意一个非实特征值
时,则对(1.1) (1.2)的任意一个非实特征值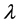 ,有
,有
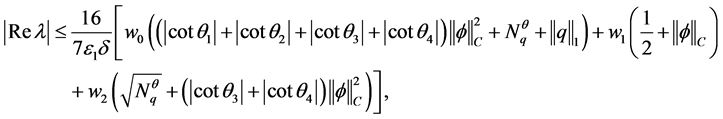 (2.10)
(2.10)
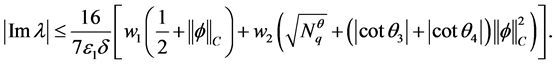 (2.11)
(2.11)
证明:在方程(2.1)的两边同时乘以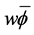 ,然后在
,然后在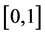 上进行积分,可得
上进行积分,可得
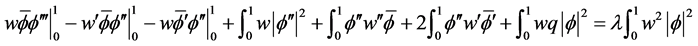
由(2.2),有

根据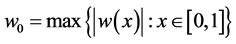 ,
, ,
,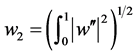 ,引理2.3和Cauchy-Schwarz不等式可得
,引理2.3和Cauchy-Schwarz不等式可得
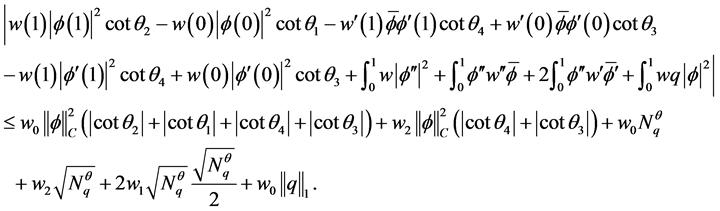 (2.12)
(2.12)
回顾(2.5)中 的定义,可知
的定义,可知
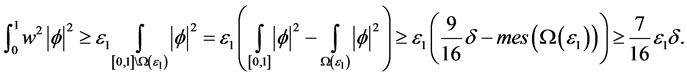
再由(2.12)可知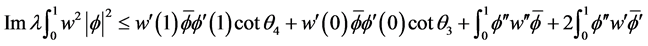 。即可得到(2.10) (2.11),定理得证。
。即可得到(2.10) (2.11),定理得证。
在下面的定理中,将考虑 仅变号一次的情况,即对于
仅变号一次的情况,即对于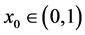
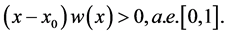 (2.13)
(2.13)
选择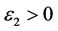 ,使得
,使得
 (2.14)
(2.14)
定理2.6 假设(2.13)成立,则对(1.1) (1.2)的任意一个非实特征值 ,有
,有
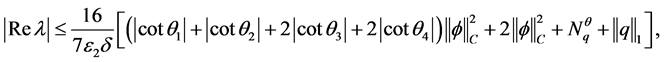 (2.15)
(2.15)
 (2.16)
(2.16)
证明:在方程(2.1)的两边同时乘以 ,并在
,并在 上进行积分,可得
上进行积分,可得

由(2.2),有
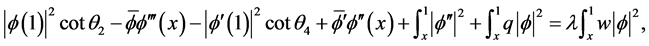
再根据(2.3),有
 (2.17)
(2.17)
对(2.17)式的实部与虚部分离得到
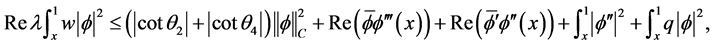 (2.18)
(2.18)
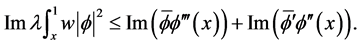 (2.19)
(2.19)
对(2.18)的两边在 上积分,可得
上积分,可得
 (2.20)
(2.20)
进一步得

同理,再对(2.18)的两边在 上积分,可得
上积分,可得
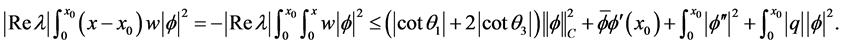
再根据(2.3)和Cauchy-Schwarz不等式得到
 (2.21)
(2.21)
再用同样的方式处理虚部,从(2.19)可得
 (2.22)
(2.22)
回顾(2.14)中 的定义,可知
的定义,可知

再由(2.21) (2.22)可得(2.15) (2.16),定理得证。
基金项目
国家自然科学基金(11661059),内蒙古自然科学基金(2017MS(LH)0103)资助。