摘要: 本文严格地证明了带扰动的Einstein-Yang/Mills方程在Holder空间中局部解的存在性,这里要求A具有零点。
Abstract:
In this paper, we will give a rigorous proof of existence of local solutions to perturbed Einstein- Yang/Mills equations with gauge group SU(2), here we require the existence of zero point for A, and we consider the area in Holder spaces.
1. 引言
Yang/Mills理论,是现代规范场理论的基础。由杨振宁和米尔斯在1954年首先提出来,通过后来许多学者于1960年到1970年代引入对称性自发破缺与渐进自由的观念,发展成今天的标准模型。杨–米尔斯理论作为克雷数学研究所提出的新前年七大问题之一,在当今物理界和数学界都是热门的问题,本文讨论静态球对称Einstein-Yang/Mills方程在Holder空间中局部解的存在性,这里Einstein度量 [1] :
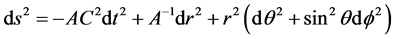 (1.1)
(1.1)
SU(2)Yang/Mills曲率-2形式 [2] :
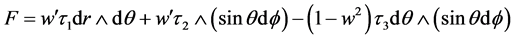 (1.2)
(1.2)
这里A,C和w都是关于r的函数,由(1.1)和(1.2),得静态球对称SU(2)EYM方程为 [3] [4] :
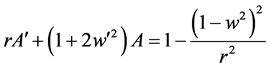 (1.3)
(1.3)
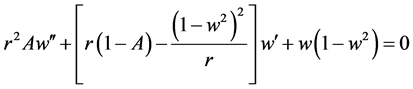 (1.4)
(1.4)
和
 (1.5)
(1.5)
由于(1.3)和(1.4)与C无关,所以本文我们主要的工作是耦合方程(1.3),(1.4)进行分析。
为了使讨论更具有一般性,对原方程加入扰动项,使得(1.4)变为:
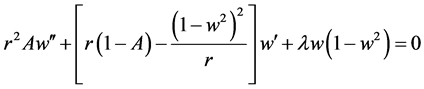 (1.6)
(1.6)
这里的 在1附近扰动。
在1附近扰动。
2. 准备知识
为了使我们讨论方便,定义函数 :
:
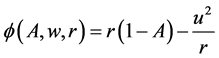 (2.1)
(2.1)
这里 。
。
设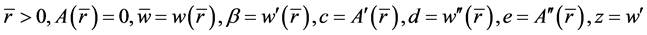 。则由(1.3),(1.6)得
。则由(1.3),(1.6)得
 (2.2)
(2.2)
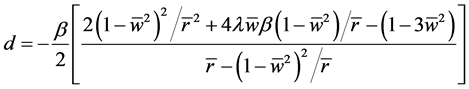 (2.3)
(2.3)
 (2.4)
(2.4)
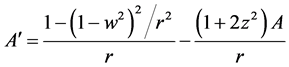 (2.5)
(2.5)
设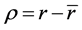 ,由泰勒展开并引入算子B有
,由泰勒展开并引入算子B有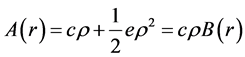 ,解得
,解得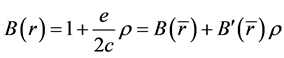 ,得
,得
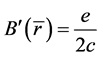 (2.6)
(2.6)
3. 局部解的存在唯一性
定理:若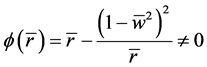 ,则对于带扰动的静态球对称EYM方程(1.3)和(1.6),在区域
,则对于带扰动的静态球对称EYM方程(1.3)和(1.6),在区域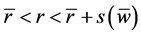 上,方程解具有存在唯一性。
上,方程解具有存在唯一性。
证明:取 ,我们考虑在Holder空间下的范数 [5] :
,我们考虑在Holder空间下的范数 [5] :
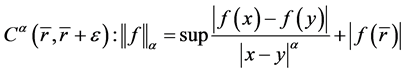
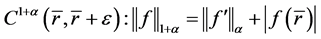

并定义集合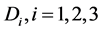 :
:
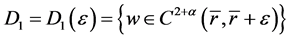

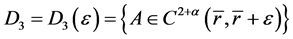
因为集合 是
是 上的闭集,易得
上的闭集,易得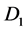 是完备的度量空间 [5] ,同理,
是完备的度量空间 [5] ,同理, 和
和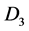 也是完备的度量空间。定义X为
也是完备的度量空间。定义X为
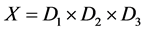
这里 ,定义度量 [5] :
,定义度量 [5] :

若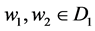 ,由于
,由于 ,则:
,则:
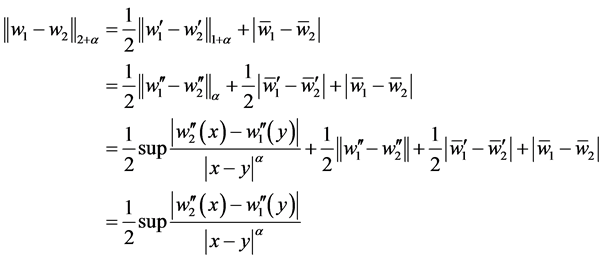
同理得
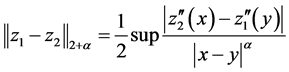
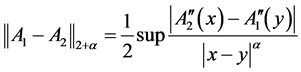
再定义映射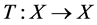 为:
为: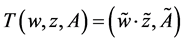 ,这里
,这里

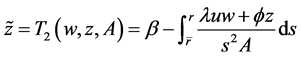
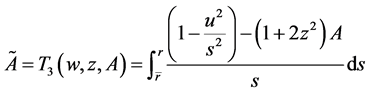
下面我们证明:对于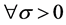 ,
, ,s.t
,s.t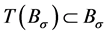 ,且T是压缩映射 [5] 。这里
,且T是压缩映射 [5] 。这里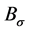 表示半径为
表示半径为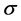 的球。用泰勒展开可得:
的球。用泰勒展开可得:
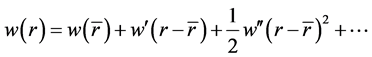
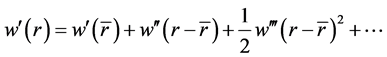
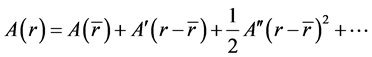
易得球上的点可表示为:
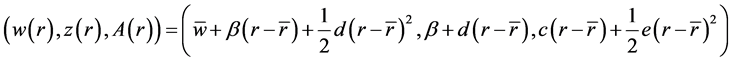
由于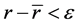 ,显然当
,显然当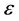 充分小时,
充分小时, ,即T为自映射得证。
,即T为自映射得证。
接下来我们证明T是压缩映射:
先考虑 ,令
,令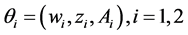 ;则
;则
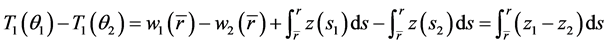
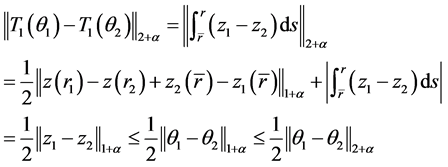
则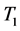 为压缩映射得证。接下来证明
为压缩映射得证。接下来证明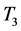 也是压缩映射:
也是压缩映射:
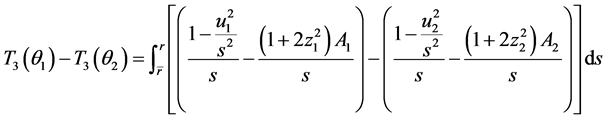
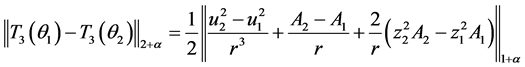
其中,对上式用推广的Holder不等式 [6] 可得

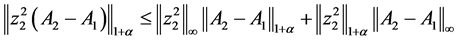

又因为当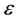 充分小时,
充分小时,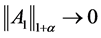 且
且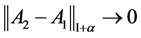 ,易得
,易得 ,即有
,即有
 ,于是
,于是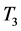 为压缩映射得证 [5] 。
为压缩映射得证 [5] 。
下面证明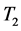 也是压缩映射。实际上
也是压缩映射。实际上
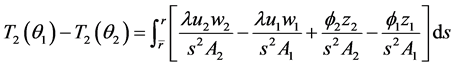
再由(2.2)可得:
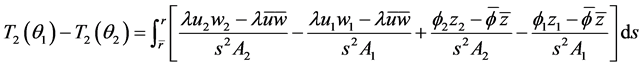
为了计算方便,我们引入算子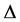 ,并定义
,并定义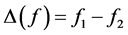 ,则上式化简为:
,则上式化简为:
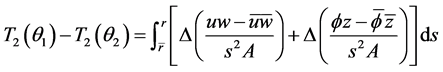
则
 (3.1)
(3.1)
由(2.6)有

则当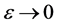 时,有
时,有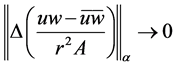 。对于(3.1)最右边部分,令
。对于(3.1)最右边部分,令
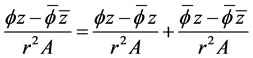 (3.2)
(3.2)
其中
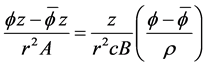
则当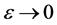 时,有
时,有 。由于
。由于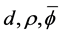 均与
均与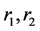 无关,故
无关,故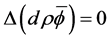 ,则对于(3.2)式最后一项,我们有
,则对于(3.2)式最后一项,我们有
 (3.3)
(3.3)
为了表示方便,令
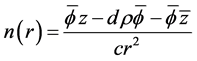
则
 (3.4)
(3.4)
其中 ,则由推广的Holder不等式有 [6] :
,则由推广的Holder不等式有 [6] :
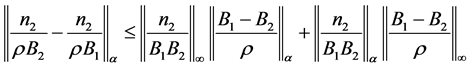
则当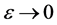 时,有
时,有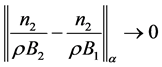 。再考虑(3.4)最右式,为表示方便令
。再考虑(3.4)最右式,为表示方便令 ,则
,则
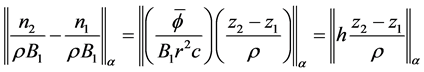
再由推广的Holder不等式 [6] 得

这里, 有界,当
有界,当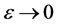 时,有
时,有 。又因为
。又因为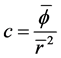 ,故
,故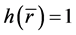 ,
,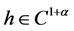 ,故
,故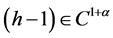 ,
, (当
(当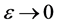 时) [6] 。于是我们可取
时) [6] 。于是我们可取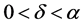 ,s.t
,s.t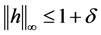 。则
。则
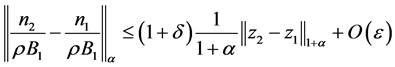
这里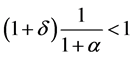 ,故可得(3.3)左式为:
,故可得(3.3)左式为:

故有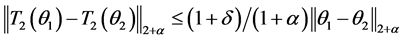 ,于是
,于是 为压缩映射得证。
为压缩映射得证。
于是,在区域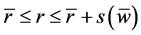 上,由Banach不动点定理,可得T存在唯一不动点 [5]
上,由Banach不动点定理,可得T存在唯一不动点 [5] 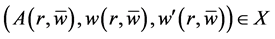 。
。