1. 引言
20世纪50年代,索洛等人 [1] [2] 提出形如
的新古典增长模型,其中
为 时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。
时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。
2011年,Matsumoto和Szidarovszky [8] 首次介绍了如下的时滞新古典增长模型
(1.1)
其中
是人均资本,
为平衡储蓄倾向,
,其中
为资本折旧率,
为劳动增长率,生产函数
(
和
是正参数),
为生产过程中的时滞。2013年,Matsumoto和Szidarovszky [9] 将模型(1.1)修改成如下形式
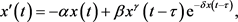 (1.2)
(1.2)
其中
为正参数,
代表资本集中度提高带来的消极影响的强度,
代表生产规模报酬率,且
,
为正常数。Matsumoto和Szidarovszky考虑了模型(1.2)分别在
时的局部稳定性。
现实生活中的系统会受到各种突发状况的影响,因此脉冲在动力系统中需加以考虑。二十世纪八十年代后,脉冲微分方程理论得到快速发展,研究成果日益丰富,可以参看文献 [11] [12] 。
本文将考察一类具有脉冲项的时滞新古典增长模型的正周期解问题,这方面的研究目前尚未见报道。
2. 预备知识
考虑如下脉冲时滞新古典增长模型
(2.1)
其中
,
,
,
为正参数,
为脉冲点。
模型(2.1)具有初值条件
(2.2)
其中
。
对于(2.1)与(2.2),提出如下假设:
H1)
是以
为周期的周期函数,
;
H2)
,
为给定的脉冲时刻,
;
H3)
为实数列,
;
H4)
为以
为周期的周期函数(这里作一个标准的假设,若因子个数为0,则乘积为1);
H5)
。
定义2.1:称定义在
上的函数
为模型(2.1)在初值条件(2.2)下的解,若
满足如下条件
i)
在
与
上绝对连续;
ii)
与
存在且
;
iii)
在
上几乎处处满足方程(2.1),在
满足脉冲条件;
iv)
。
在假设条件(H1)~(H5)下,考虑如下模型
(2.3)
其中
,
。
模型(2.3)满足初值条件
(2.4)
是模型(2.3)在初值条件(2.4)下的解,是指
是定义在
上,在
上是满足(2.3)的绝对连续函数,且在
上满足初值条件(2.4)。
定义2.2 [13] :设
为Banach空间,
称为
中的一个锥,如果它是
的非空闭子集,且满足条件
i)
ii)
蕴含
。
引理2.1 [13] (锥拉伸与锥压缩不动点定理)
设
为Banach空间
中的有界开子集,
,
为
中的一个锥,
为全连续算子,若
满足条件:
i)
(即范数锥拉伸);
ii)
(即范数锥压缩)。
则
在
中必存在不动点。
3. 主要结果
引理3.1:假设(H1)~(H5)成立,则
i)
为模型(2.3)与(2.4)的解,则
为模型(2.1)与(2.2)在
上的解;
ii)
为模型(2.1)与(2.2)的解,则
为模型(2.3)与(2.4)在
上的解。
证明:i) 设
为模型(2.3)与(2.4)的解,易知
在
及
上绝对连续,且对
,有
所以,
在
上几乎处处满足方程(2.1)。
对每个
,有
因此,对于每个
有
。
且在
上,有
。因此
为模型(2.1)与(2.2)在
上的解。
ii)设
是模型(2.1)与(2.2)的解,所以
在
与
上是绝对连续的。因此,
在
与
上也是绝对连续的。
对
,有
,
且
,则
是连续的且易知在
上绝对连续,由(i)类似可证
为(2.3)在
上满足初值条件(2.4)的解。
推论3.1:假设条件(H1)~(H5)成立,则
i)
为(2.3)与(2.4)的
-周期解,则
为(2.1)与(2.2)在
上的正
-周期解;
ii)
为(2.1)与(2.2)的
-周期解,则
为(2.3)与(2.4)在
上的正
-周期解。
证明:由引理3.1以及假设条件(H1),(H4)即可得证。
注3.1:由推论3.1可知,讨论具有脉冲影响的时滞新古典增长模型(2.1)的
-正周期解,只需要转化为讨论不具有脉冲的时滞新古典增长模型(2.3)的
-正周期解。
为应用引理2.1,令
,赋予范数
,则
为Banach空间。
令
,其中
为后面所定义的正常数,则
为
中的锥。定义算子
(3.1)
其中
,
,
。记
以下为方便计,对于
-周期函数
,采用如下符号
,
。
注3.2:由引理2.1知,对于
,
是
上的全连续算子,且易证模型(2.3)的正
-周期解的存在性等价于求
在
上的不动点。
注3.3:引入函数
,则易知
在
上严格单调递增,在
上严格单调递减,则知
在点
取得最大值,且存在唯一的
,使得
。
引理3.2:假设条件(H1)~(H5)成立,则
为全连续算子。
证明:由假设,
为连续的
-周期函数。且易验证
,
,有
,
所以,
。因此
。
下证
为全连续的。显然
是连续的。又,可得
,
以及,
因此
是紧的,从而
为全连续的。
定理3.1:假设条件(H1)~(H5)成立,再假设条件(H6)
成立,则方程(2.3)在初值条件(2.4)下存在两个正周期解。
证明:因为
,则存在两个正常数
Math_190#,以及存在一个充分小满足
的
,使得
(3.2)
(3.3)
定义
,当
时,有
且
,由(3.1)和(3.2),得
,
因此,
,
。
定义
,当
时,有
,
,因为
,从而由条件(H6),有
因此,
,
。
定义
,其中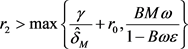 ,
,
,当
时,有
,
。则由(3.1)和(3.3),得
因此,
,
,其中
,
。
因为
,且由引理3.2知,
,
是全连续的,因此,由引理2.1,得到
在
上存在不动点
,在
上存在另一个不动点
。又因为
,
,因此
与
为模型(2.3)在初值条件(2.4)下的两个不同的正周期解。
由引理3.1,可知模型(2.1)在初值条件(2.2)下存在两个不同的正周期解。
4. 具体实例
考虑下列脉冲时滞新古典增长模型
(4.1)
其中取脉冲
,脉冲时刻为
。令
,则有
因此
是以
为周期的函数。
由
,
,
,
,
,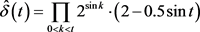 ,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。
,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。