弱链对角占优B-矩阵线性互补问题误差界的新估计式

A New Error Bound for Linear Complementarity Problems for Weakly Chained Diagonally Dominant B-Matrices

摘要: 本文利用弱链对角占优M-矩阵逆矩阵无穷范数上界的估计式，结合不等式放缩技术，给出弱链对角占优B-矩阵线性互补问题误差界的一个新估计式。数值算例表明，新估计式改进了现有的几个结果。

Abstract: In this paper, by the infinity norm bound of inverse matrix of weakly chained diagonally dominant M-matrices, we give a new error bound for the linear complementarity problem when the matrix involved is a weakly chained diagonally dominant B-matrix, which improves some existing ones. Numerical examples are given to show the corresponding results.

1. 引言

线性互补问题在力学、交通、经济、金融和控制等诸多领域具有广泛应用，如市场均衡问题、最优停止问题、期权定价问题、弹性接触问题和自由边界问题等 [1] [2] [3] [4] 。线性互补问题( $LCP\left(M,q\right)$ )是指求 $x\in R^n$ ，满足

$x\ge 0,Mx+q\ge 0,{\left(Mx+q\right)}^{\text{T}}x=0$

其中 $M\in R^{n\times n}$ 为实矩阵，实向量 $q\in R^n$ 。众所周知，当矩阵M为P-矩阵(所有主子式都是正的 [1] )时， $LCP\left(M,q\right)$ 不仅存在唯一解 [2] ，而且易于误差分析 [4] 。2006年，陈小君等给出P-矩阵线性互补问题的误差界 [5] ：

${\Vert x-x^{*}\Vert }_{\infty }\le \underset{d\in {\left[0,1\right]}^n}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }{\Vert r\left(x\right)\Vert }_{\infty }$ (1)

其中 $r\left(x\right)=\min \left\{x,Mx+q\right\}$ 为向量 $x$ 与 $Mx+q$ 对应位置分量最小值， $D=diag\left(d_i\right)$ 。不难发现，求解误差界(1)中的最小化问题 $\underset{d\in {\left[0,1\right]}^n}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }$ 十分困难。因此，近年来有众多专家和学者关注于误差界的估计问题，并给出了一些简单易算的估计式 [6] - [13] 。本文将研究P-矩阵的一个重要子类——弱链对角占优B-矩阵的线性互补问题的误差界估计问题，应用弱链对角占优M-矩阵的逆矩阵无穷范数上界的估计式，得到弱链对角占优B-矩阵线性互补问题误差界的一个新估计式。数值算例表明，新估计式改进了现有的几个结果。

2. 预备知识

令 $C^{n\times n}$ ( $R^{n\times n}$ )表示所有n阶复矩阵(实矩阵)构成的集合，指标集 $N=\left\{1,2,\cdots ,n\right\}$ 。设 $A=\left[a_{ij}\right]\in R^{n\times n}$ ，对任意的 $i,j,k\in N,i\ne j$ ，记

$R_i\left(A\right)={\displaystyle \underset{j\ne i}{\sum }\left|a_{ij}\right|}$ ， $u_i\left(A\right)=\frac{1}{\left|a_{ii}\right|}{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|a_{ij}\right|}$ ，

$h_l^{\left(k-1\right)}={\displaystyle \underset{j=k}{\overset{l-1}{\sum }}\left|a_{lj}\right|}\cdot \frac{h_j^{\left(k-1\right)}}{\left|a_{jj}\right|}+{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|a_{ij}\right|}$ (2)

$c_k=\underset{k\le i\le n}{\max }\left\{\frac{h_i^{\left(k-1\right)}}{\left|a_{ii}\right|}\right\},k=1,2,\cdots ,n$ ，

$q_k\left(A\right)=\underset{1\le i\le n-k}{\max }\left\{\frac{\left|a_{i+k,k}\right|+{\displaystyle \underset{h=k+1,h\ne i+k}{\overset{n}{\sum }}\left|a_{i+k,k}\right|c_k}}{\left|a_{i+k,i+k}\right|}\right\},k=1,2,\cdots ,n$ .

定义1 [14] ：设 $A=\left[a_{ij}\right]\in C^{n\times n}$ ，若对任意的 $i\in N$ ，有

$\left|a_{ii}\right|\ge R_i\left(A\right)$ ，

且对每个 $i\notin J\left(A\right)=\left\{i\in N:\left|a_{ii}\right|>R_i\left(A\right)\right\}\ne \varphi$ 存在非零元素链 $a_{i{i}_1},a_{i_1{i}_2},\cdots ,a_{i_{r}j}$ 满足 $j\in J\left(A\right)$ ，则称A为弱链对角占优矩阵。

定义2 [15] ：设 $A=\left[a_{ij}\right]\in R^{n\times n}$ ，记 $M=B^{+}+C$ ，其中

$B^{+}=\left[b_{ij}\right]=\left(\begin{array}{ccc}{m}_{11}-r_1^{+}& \dots & m_{1n}-r_1^{+}\\ ⋮& \ddots & ⋮\\ m_{n1}-r_n^{+}& \cdots & m_{nn}-r_n^{+}\end{array}\right)$ , $r_i^{+}=\max \left\{0,m_{ij}|j\ne i\right\}$ , (3)

若 $B^{\text{+}}$ 为弱链对角占优矩阵且所有的主对角元素皆为正，则称 $A$ 为弱链对角占优矩阵。

文献 [15] 给出结果：设 $M=\left[m_{ij}\right]\in R^{n\times n}$ 是弱链对角占优B-矩阵，记 $M=B^{\text{+}}\text{+}C$ ，其中 $B^{+}=\left[b_{ij}\right]$ 形如(3)式，则

$\underset{d\in {\left[0,1\right]}^n}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }\le {\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{n-1}{\min \left\{{\bar{\beta }}_i,1\right\}}{\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{b_{jj}}{{\bar{\beta }}_j}}}$ ， (4)

其中 ${\bar{\beta }}_i=b_{ii}-{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|b_{ij}\right|}>0$ 且 ${\displaystyle \underset{j=1}{\overset{\text{0}}{\prod }}\frac{b_{jj}}{{\bar{\beta }}_j}}=1$ 。

为了给出本文结论，先介绍几个预备引理：

引理1 [16] ：设 $A=\left[a_{ij}\right]\in R^{n\times n}$ 是弱链对角占优M-矩阵， $u_k{q}_k<1,k=1,\cdots ,n$ ，则

$\begin{array}{l}{\Vert A^{-1}\Vert }_{\infty }\le \max \{\frac{1}{a_{11}\left(1-u_1{q}_1\right)}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{1}{a_{ii}\left(1-u_i{q}_i\right)}{\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{u_j\left(A\right)}{1-u_j\left(A\right)q_j\left(A\right)}}\right]},\\ {\displaystyle \underset{i=2}{\overset{n}{\sum }}\frac{q_1}{a_{11}\left(1-u_1{q}_1\right)}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{q_i}{a_{ii}\left(1-u_i{q}_i\right)}{\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{1}{1-u_j{q}_j}}\right]}}\}\end{array}$ ,

其中 $u_j\left(A\right)$ ， $q_j\left(A\right)$ 如(2)式所定义。

引理2 [11] ：设 $\gamma >0$ 和 $\eta \ge \text{0}$ ，则对任意的 $x\in \left[0,1\right]$ ，有

$\frac{1}{1-x-\gamma x}\le \frac{1}{\min \left\{\gamma ,1\right\}}$ ， $\frac{\eta x}{1-x\text{+}\gamma x}\le \frac{\eta }{\gamma }$ .

3. 主要结果

本节给出弱链对角占优B-矩阵线性互补问题误差界新的上界估计式，并和现有结果进行比较。首先给出一个引理：

引理3：设矩阵 $M=\left[m_{ij}\right]\in R^{n\times n}$ 主对角元全为正，记 $M=B^{+}+C$ ，其中 $B^{+}$ 形如(3)式。令 $B_D=I-D+D{B}^{+}=\left[{\bar{b}}_{ij}\right]$ ，则对任意的 $k=1,2,\cdots ,n$ , $l=k,k+1,\cdots ,n$ 有

$\frac{h_l^{\left(k-1\right)}\left(B_D^{+}\right)}{\left|{\bar{b}}_{ll}\right|}\le \frac{h_l^{\left(k-1\right)}\left(B^{+}\right)}{\left|b_{ll}\right|}$ ，(5)

其中 $h_l^{\left(k-1\right)}$ 如(2)式所定义。

证明：下面利用数学归纳法证明(5)式成立。

情形一：k = 1，此时 $l=1,2,\cdots ,n$ 。

当l = 1时，

$\frac{h_1^{\left(0\right)}\left(B_D^{+}\right)}{\left|{\bar{b}}_{11}\right|}\text{=}\frac{d_1{\displaystyle \underset{j=2}{\overset{n}{\sum }}\left|b_{1j}\right|}}{1-d_1+d_1{b}_{11}}\le \frac{{\displaystyle \underset{j=2}{\overset{n}{\sum }}\left|b_{1j}\right|}}{b_{11}}=\frac{h_1^{\left(0\right)}\left(B^{+}\right)}{\left|b_{11}\right|}$ ，

假设当 $l=i\left(2<i<n\right)$ 时， $\frac{h_i^{\left(0\right)}\left(B_D^{+}\right)}{\left|{\bar{b}}_{ii}\right|}\le \frac{h_i^{\left(0\right)}\left(B^{+}\right)}{\left|{\bar{b}}_{ii}\right|}$ 式成立，现证 $l=i+\text{1}$ 时(5)式也成立，利用引理2易证

$\frac{h_{i+1}^{\left(0\right)}\left(B_D^{+}\right)}{\left|{\bar{b}}_{i+1,i+1}\right|}=\frac{{\displaystyle \underset{j=k}{\overset{n}{\sum }}\frac{\left|{\bar{b}}_{i+1,j}\right|}{\left|{\bar{b}}_{jj}\right|}\cdot h_j^{\left(0\right)}\left(B_D^{+}\right)}+{\displaystyle \underset{j=i+2}{\overset{n}{\sum }}\left|{\bar{b}}_{i+1,j}\right|}}{\left|{\bar{b}}_{i+1,i+1}\right|}\le \frac{h_{i+1}^{\left(0\right)}\left(B^{+}\right)}{\left|b_{i+1,i+1}\right|}$ .

因此，对于 $l=1,2,\cdots ,n$ ，有 $\frac{h_l^{\left(0\right)}\left(B_D^{+}\right)}{\left|{\bar{b}}_{ll}\right|}\le \frac{h_l^{\left(0\right)}\left(B^{+}\right)}{\left|b_{11}\right|}$ 。

情形二：当 $k=2,3,\cdots ,n$ 时，同理可证(5)式成立。

综合情形一与情形二，结论成立。

定理1：设 $M\in R^{n\times n}$ 是弱链对角占优B-阵， $M=B^{+}+C$ ，其中 $B^{+}=\left[b_{ij}\right]$ 形如(3)式。若 $u_k\left(B^{+}\right)q_k\left(B^{+}\right)<1$ ， $k=1,\cdots ,n$ ，则

$\begin{array}{l}\underset{d\in {[0,1]}^n}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }\\ \le \left(n-1\right)\cdot \max \{\frac{1}{\min \left\{{\alpha }_1\left(B^{+}\right),1\right\}}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{1}{\min \left\{{\alpha }_i\left(B^{+}\right),1\right\}}\cdot {\displaystyle \underset{j=1}{\overset{n}{\prod }}\frac{b_{jj}\cdot u_j\left(B^{+}\right)}{{\alpha }_i\left(B^{+}\right)}}\right]},\\ \frac{q_1\left(B^{+}\right)}{\min \left\{{\alpha }_1\left(B^{+}\right),1\right\}}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{q_i\left(B^{+}\right)}{\min \left\{{\alpha }_i\left(B^{+}\right),1\right\}}\cdot {\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{b_{jj}}{{\alpha }_j\left(B^{+}\right)}}\right]}\}\end{array}$ (6)

其中 ${\alpha }_i\left(B^{+}\right)=b_{ii}-{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|b_{ij}\right|}\cdot q_i\left(B^{+}\right)$ ， $q_i\left(B^{+}\right)$ 由(2)式所给。

证明：令 $M_D=I-D+DM$ ，则

$M_D=I-D+DM=I-D+D\left(B^{+}+C\right)=B_D^{+}+C_D$ ，其中 $B_D^{+}=I-D+D{B}^{+}$ ， $C_D=DC$ 。由文献 [15] 中的定理2知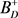，是弱链严格对角占优M-阵

${\Vert M_D^{-1}\Vert }_{\infty }\le \left(n-1\right)\cdot {\Vert {\left(B_D^{+}\right)}^{-1}\Vert }_{\infty }$ . (7)

由引理1知

$\begin{array}{l}{\Vert {\left(B_D^{+}\right)}^{-1}\Vert }_{\infty }\le \max \{\frac{1}{{\bar{b}}_{11}\left[1-u_1\left(B_D^{+}\right)q_1\left(B_D^{+}\right)\right]}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{1}{{\bar{b}}_{ii}\left[1-u_i\left(B_D^{+}\right)q_i\left(B_D^{+}\right)\right]}\cdot {\displaystyle \underset{j=1}{\overset{n}{\prod }}\frac{u_j\left(B_D^{+}\right)}{1-u_j\left(B_D^{+}\right)q_j\left(B_D^{+}\right)}}\right]},\\ \frac{q_1\left(B_D^{+}\right)}{{\bar{b}}_{11}\left[1-u_1\left(B_D^{+}\right)q_1\left(B_D^{+}\right)\right]}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{q_i\left(B_D^{+}\right)}{{\bar{b}}_{ii}\left[1-u_i\left(B_D^{+}\right)q_i\left(B_D^{+}\right)\right]}\cdot {\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{1}{1-u_j\left(B_D^{+}\right)q_j\left(B_D^{+}\right)}}\right]}\}\end{array}$ .

由引理2和引理3，得

$u_i\left(B_D^{+}\right)=\frac{{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|b_{ij}\right|d_i}}{1-d_i+b_{ii}{d}_i}\le \frac{{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|b_{ij}\right|}}{b_{ii}}=u_i\left(B^{+}\right)$ ，

$\begin{array}{c}{q}_k\left(B_D^{+}\right)=\underset{1\le i\le n-k}{\max }\left\{\frac{\left|{\bar{b}}_{i+k,k}\right|+{\displaystyle \underset{h=k+1,h\ne i+k}{\overset{n}{\sum }}\left|{\bar{b}}_{i+k,h}\right|}\cdot {\bar{c}}_k}{\left|{\bar{b}}_{i+k,i+k}\right|}\right\}\\ \le \underset{1\le i\le n-k}{\max }\frac{d_{i+k}\left[\left|b_{i+k,k}\right|+{\displaystyle \underset{h=k+1,h\ne i+k}{\overset{n}{\sum }}\left|b_{i+k,h}\right|}\cdot c_k\right]}{1-d_{i+k,i+k}+d_{i+k,i+k}\left|b_{i+k,i+k}\right|}\\ \le \underset{1\le i\le n-k}{\max }\left\{\frac{\left|b_{i+k,k}\right|+{\displaystyle \underset{h=k+1,h\ne i+k}{\overset{n}{\sum }}\left|b_{i+k,h}\right|}\cdot c_k}{\left|b_{i+k,i+k}\right|}\right\}=q_k\left(B^{+}\right)\end{array}$ ,

$\begin{array}{c}\frac{1}{{\bar{b}}_{ii}\left[1-u_i\left(B_D^{+}\right)\cdot q_i\left(B_D^{{}^{+}}\right)\right]}=\frac{1}{{\bar{b}}_{ii}-{\bar{b}}_{ii}\cdot u_i\left(B_D^{+}\right)\cdot q_i\left(B_D^{{}^{+}}\right)}\\ \le \frac{1}{{\bar{b}}_{ii}-{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|{\bar{b}}_{ij}\right|}\cdot q_i\left(B^{+}\right)}\\ \le \frac{1}{\min \left\{b_{ii}-{\displaystyle \underset{j=i+1}{\overset{n}{\sum }}\left|b_{ij}\right|}\cdot q_i\left(B^{+}\right),1\right\}}\\ =\frac{1}{\min \left\{{\alpha }_i\left(B^{+}\right),1\right\}}\end{array}$ ,

及

$\frac{1}{1-u_j\left(B_D^{{}^{+}}\right)\cdot q_j\left(B_D^{{}^{+}}\right)}\le \frac{b_{jj}}{b_{jj}-{\displaystyle \underset{k=j+1}{\overset{n}{\sum }}\left|b_{jk}\right|\cdot q_j\left(B^{+}\right)}}=\frac{b_{jj}}{{\alpha }_j\left(B^{+}\right)}$ .

则

$\begin{array}{l}{\Vert {\left(B_D^{+}\right)}^{-1}\Vert }_{\infty }\le \max \{\frac{1}{\min \left\{{\alpha }_1\left(B^{+}\right),1\right\}}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{1}{\min \left\{{\alpha }_i\left(B^{+}\right),1\right\}}\cdot {\displaystyle \underset{j=1}{\overset{n}{\prod }}\frac{b_{jj}\cdot u_j\left(B^{+}\right)}{{\alpha }_i\left(B^{+}\right)}}\right]},\\ \frac{q_1\left(B^{+}\right)}{\min \left\{{\alpha }_1\left(B^{+}\right),1\right\}}+{\displaystyle \underset{i=2}{\overset{n}{\sum }}\left[\frac{q_i\left(B^{+}\right)}{\min \left\{{\alpha }_i\left(B^{+}\right),1\right\}}\cdot {\displaystyle \underset{j=1}{\overset{i-1}{\prod }}\frac{b_{jj}}{{\alpha }_j\left(B^{+}\right)}}\right]}\}\end{array}$ .(8)

由(7)式和(8)式可知，(6)式成立。

4. 数值算例

例：考虑弱链对角占优B-矩阵 [15] ：

$M=\left[\begin{array}{cccc}1.\text{5}& 0.\text{2}& 0.\text{4}& 0.\text{5}\\ -\text{0}\text{.1}& 1.5& 0.5& 0.1\\ 0.5& -0.1& 1.5& 0.1\\ 0.4& 0.4& 0.8& 1.8\end{array}\right]$ ,

令 $M=B^{\text{+}}+C$ ，其中

$B^{\text{+}}=\left[\begin{array}{cccc}1& -0.\text{3}& -0.1& 0\\ -0.6& 1& 0& -0.4\\ 0& -0.6& 1& -0.4\\ -0.4& -0.4& 0& 1\end{array}\right]$ .

由(4)式得

$\underset{d\in {\left[0,1\right]}^4}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }\le \text{41}\text{.1111},$

由文献 [17] 中的(5)式得

$\underset{d\in {\left[0,1\right]}^4}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }\le \text{38}\text{.6334},$

由应用定理1中的(6)式得

$\underset{d\in {\left[0,1\right]}^4}{\max }{\Vert {\left(I-D+DM\right)}^{-1}\Vert }_{\infty }\le \text{10}\text{.4724}$ .

显然，(7)式优于(4)式和文献 [17] 中的(5)式。

基金项目

陕西省自然科学基础研究计划项目(2017JQ3020)；陕西省高校科协青年人才托举基金(20160234)；宝鸡文理学院重点项目(ZK2017095, ZK2017021)。