宽广温度压强下Rb_xC₆₀ (x = 3,4,6)的热力学性质

Thermodynamic Properties of Rb_xC₆₀ (x = 3,4,6) at Wide Temperature and Pressure

摘要: 本文基于自由体积理论(FVT)应用解析平均场近似的方法对Rb_xC₆₀ (x = 3,4,6)的热力学性质进行研究。根据双指数势模型和文献中的压缩实验数据，拟合得到三套势参数，并对相应的势函数曲线进行了比较分析。在宽广温度和压强下对三种碱金属掺杂富勒烯Rb_xC₆₀ (x = 3,4,6)的热力学量，包括热膨胀、体积模量、等容热容量、亥姆霍兹自由能进行了计算和分析。我们采用的方法不仅计算简单而且结果与文献中实验数据非常一致。

Abstract: Based on the free volume theory (FVT), the thermodynamic properties of Rb_xC₆₀ (x = 3,4,6) are studied by means of analytic mean field approximation. According to the double exponential po-tential model and the compression experimental data in the literature, three sets of potential pa-rameters are obtained, and the corresponding potential function curves are compared and ana-lyzed. The thermodynamic properties of three alkali metal doped fullerene Rb_xC₆₀ (x = 3,4,6), in-cluding thermal expansion, bulk modulus, constant volume heat capacity and Helmholtz free en-ergy, were calculated and analyzed under wide temperature and pressure. Our method is not only simple in calculation, but also in good agreement with the experimental data in the literature.

1. 引言

近二十年来，富勒烯C₆₀及其衍生物得到了人们的广泛关注。这是因为它们不仅具有奇妙的分子结构，而且其固相还具有迷人的晶体结构、力学和电学等性质。C₆₀分子呈球笼状，60个碳原子对称等价地分布其上 [1] 。在高温下，C₆₀以面心立方(fcc)结构呈现，分子自由高速转动。在温度低于260 K，晶格转化为简单立方(sc)结构，低于90 K时冻结为玻璃相 [2] 。富勒烯C₆₀及其衍生物的发现和制备不仅在理论上取得了巨大进展，而且在实践上也开拓了很多新的领域，从而导致新的产业和产品的出现。特别是最近几年来，人们对碱金属掺杂富勒烯进行了大量的研究工作，在实验和理论上取得了重大的成果。在研究中，人们主要集中于对其结构和电磁性质的研究 [3] 。三种碱金属掺杂富勒烯Rb ₃C ₆₀，Rb ₄C ₆₀和Rb ₆C ₆₀表现出不同的性质，面心立方结构Rb ₃C ₆₀具有金属和超导体的性质，体心正方结构Rb ₄C ₆₀具有绝缘性能，体心立方结构Rb ₆C ₆₀是绝缘体 [4] 。目前，只有几项关于Rb_xC₆₀ (x = 3,4,6)的热力学性质的报道 [5] [6] [7] [8] 。研究小组测得了Rb ₃C ₆₀的实验状态方程，并采用通用状态方程对热物性进行了研究，但这些方程适用的温度压强范围有限，不能很好考虑温度效应。虽然Rb ₄C ₆₀在0.8 GPa时发生Mott相变引起人们的极大兴趣，但迄今为止还没有更多压缩实验数据的最新报道。Poloni小组 [9] 对Rb ₆C ₆₀和Cs ₆C ₆₀体系性质在实验和理论方面进行了研究，得到了一些有用的结论。Sabouri-Dodaran等 [10] 利用x-ray射线衍射实验得到了Rb_xC₆₀ (x = 3,4,6)的实验状态方程，并用ab initio对其热力学性质进行计算。但人们对Rb_xC₆₀ (x = 3,4,6)高温高压下的热力学性质研究相对较少。在理论方面人们大多基于在谐性或准谐性近似下进行计算，不能很好地考虑材料在高温下的非简谐效应。本文基于自由体积模型并应用解析平均场方法可以方便地导出Rb_xC₆₀ (x = 3,4,6)的解析状态方程和能量的表达式，该方法不仅物理意义清晰，而且便于计算，可以对材料在超出实验条件的温度压力下的性质做出合理预测。

2. 自由体积模型

自由体积模型 [11] (亦称胞腔模型)是一种平均场近似，通常是考虑原子对晶相的劾姆赫兹自由能的热贡献。该模型认为每一个原子被限制在由它周围最近邻原子形成的Wigner-Seitz (WS)元胞中心。研究表明虽然这种元胞模型忽略了原子间的相互关联，但它包含了高温下重要的非简谐项。它能对硬球型固体、方井固体、面心立方LJ晶系、六指数势模型固体和氯化钠等的热力学性质进行很好的描述。十年前，王义等 [12] 提出了解析平均场方法并成功应用于许多的物质。孙等 [13] 证明了这种方法是FVT的一种解析近似，它与FVT是等效的。在根据FVT不能导出解析状态方程或者进行平均场积分太复杂的情况下，采用解析平均场方法就非常方便。根据解析平均场近似模型和元胞理论，将粒子热运动的自由能表示为

$F=F\left(V,T\right)=-NkT\left[\frac{3}{2}\ln \left(2\pi \mu kT/h^2\right)+\ln v_f\right]$ (1)

胞中心粒子是在周围粒子作用形成的平均场中运动，其自由运动的有效体积(即自由容积)可表示为

$v_f=v_f\left(V,T\right)=4\pi {\displaystyle {\int }_0^{r_m}\exp \left[-g\left(r,V\right)/kT\right]}{r}^{2}dr$ (2)

$g\left(r,V\right)$ 表示某一分子漂移距中心分子为 $r$ 时的势能。基于物理意义上的考虑，用这种近似方法将平均势能用冷能来表示，可以很方便地建立Rb_xC₆₀ (x = 3,4,6)的解析状态方程并对其热力学性质研究。

3. 势函数的选取

研究表明，指数势能很好的描述固态富勒烯、金刚石、立方氮化硼等材料在宽广温度和压力下的热力学性质 [14] 。由于Rb_xC₆₀ (x = 3,4,6)分子内的振动对状态方程和热力学性质(热容量除外)影响很小，所以我们也只考虑分子之间相互作用对状态方程和热力学性质的贡献。因此，本文采用双指数势描述Rb_xC₆₀ (x = 3,4,6)分子间的相互作用。该势函数的表达式如下

$\epsilon \left(s\right)={\epsilon }_0\cdot \left[C_1{e}^{{\lambda }_1\left(1-s\right)}+C_2{e}^{{\lambda }_2\left(1-s\right)}\right],s=r/r_0$ (3)

$\{\begin{array}{l}{C}_1={\lambda }_2/\left({\lambda }_1-{\lambda }_2\right)\hfill \\ C_2=-{\lambda }_1/\left({\lambda }_1-{\lambda }_2\right)\hfill \end{array}$ (4)

式中 $r$ 是径向坐标， $r_0$ 是分子间平衡距离， ${\epsilon }_0$ 是势阱深度，两个势参数 ${\lambda }_1$ ， ${\lambda }_2$ 描述势能随径向坐标r的变化。

4. 计算结果分析

运用解析平均场方法得到的解析状态方程和热力学量的表达式，我们对Rb_xC₆₀ (x = 3,4,6)的热力学性质进行了计算和分析。美国学者Girifalco [15] 指出，在C₆₀分子中原子间是强烈的共价键相互作用构成高度对称的球笼状分子，而分子间是较弱的范德瓦尔斯相互作用。因此固态C₆₀的热物理性质可以视为分子内和分子间的振动贡献之和，而分子内振动对状态方程和热物理量(热容量除外)的贡献可以忽略，所以没有把这部分贡献考虑在状态方程和热力学性质中。因此，在本文中我们也仅仅考虑Rb_xC₆₀ (x = 3,4,6)分子之间相互作用对状态方程和热力学性质的贡献。Sabouri-Dodaran等 [10] 在室温(取为296 K)不同压强范围分别测得了这三种材料的压缩数据。考虑到Rb ₃C ₆₀是fcc结构、Rb ₄C ₆₀是bct结构和Rb ₆C ₆₀是bcc结构的特点，我们拟合实验数据得到三套势参数。在图1中给出了实验数据和拟合曲线，从该图可以看出对三种材料的压缩实验数据拟合的效果很好，这说明解析平均场方法对于研究Rb_xC₆₀ (x = 3,4,6)的热力学性质是一种很适用的方法。本文还分别给出了它们在温度为2800 K时的密度随压强的变化趋势，由图1可以看出三种材料的密度随压强的增大而增大，随温度升高而减小。

根据Rb_xC₆₀ (x = 3,4,6)的压缩实验数据，通过拟合得到三组势参数。在图2中，给出了Rb ₃C ₆₀、Rb ₄C ₆₀和Rb ₆C ₆₀的所对应的三条势函数曲线。从图2可以看出它们对应的势阱深度分别约为3630 K、12850 K和36000 K，这说明Rb ₆C ₆₀分子间的相互作用强于Rb ₃C ₆₀分子间和Rb ₄C ₆₀分子间的相互作用，该结果与实验结论一致。同时从图2还可以发现，三条势函数曲线间的变化趋势的差异在高压下很小但在低压下明显一些，在双指数势的吸引部分Rb ₆C ₆₀比Rb ₃C ₆₀和Rb ₄C ₆₀的势函数曲线的斜率更大，表明Rb ₆C ₆₀的势阱深度随r变化很快。Sabouri-Dodaran等 [10] 利用第一性原理计算出的状态方程与Rb_xC₆₀ (x = 3,4)的实验测量数据符合很好，同时他们还根据实验数据分别利用不同的通用状态方程得到了Rb_xC₆₀ (x = 3,4,6)的体积模量及对压强的变化率，但结果稍有差异。对于fcc Rb ₃C ₆₀，考虑到室温下元胞参数为1.442 ± 0.002 nm [10] ，我们得到的体积模量13.7 GPa与Sabouri-Dodaran分别采用的线性拟合(15.0 ± 2 GPa)、Murnaghan

Figure 1. Compression curves at 296 K and 2800 K, experimental data [10] (small circle)

图1. 在296 K和2800 K的压缩曲线，实验数据 [10] (小圆圈)

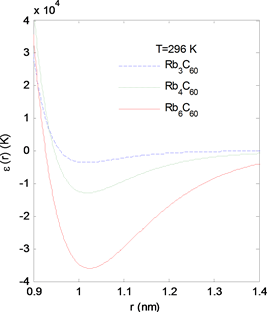
Figure 2. Potential function curves of Rb_xC₆₀ (x = 3,4,6)

图2. Rb_xC₆₀ (x = 3,4,6)的势函数曲线

方程(13.65 ± 1.2 GPa)以及Vinet方程(11.7 ± 1.5 GPa)符合很好。从我们的计算结果可以看出在低压下三种掺杂物中Rb ₃C ₆₀最软而Rb ₆C ₆₀最硬。尽管Rb ₄C ₆₀具有很大的自由体积(元胞体积减去分子体积)，但它比Rb ₃C ₆₀更硬(分别为24.8 GPa和13.7 GPa)比Rb ₆C ₆₀ (44.9 GPa)软。图3表示温度分别为296 K和2800 K时Rb_xC₆₀ (x = 3,4,6)的等温体积模量B_T相对于压强P的变化。当温度一定时B_T随压强的增大而增大，当压强一定时B_T随温度的升高而减小，这表明增大压强和降低温度对体积模量有着相同的效果。三种掺杂物的体积模量在低压差异较小，但在高压差距较为明显。

自由能F是重要的热力学量，根据自由能很容易得到其它的热力学量的表达式。因此，在图4中我们给出了在四个温度(296 K、600 K、1000 K、1500 K)下自由能相对于密度r的变化。图4表明在四个不同的温度下Rb_xC₆₀ (x = 3,4,6)的自由能是密度的增函数，具有相同的变化趋势，在低温时比在高温时变化更快。

Figure 3. Variations of bulk modulus versus pressure

图3. 体积模量随压强的变化

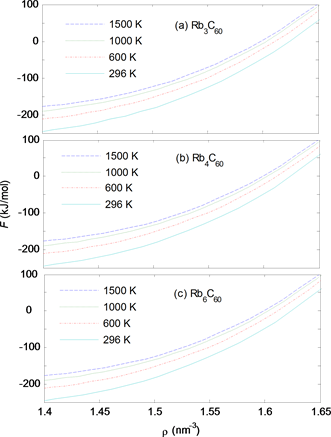
Figure 4. Variations of free energy versus density

图4. 自由能随密度的变化

Table 1. The nearest-neighbor distance a in nm, linear thermal expansion coefficient α in 10−5 K−1, the bulk modulus BT in GPa, the heat capacity CV in kJ∙mol−1∙K−1

表1. 在零压下的热力学性质：最近紧邻距离a (nm)，线性热膨胀系数α (10⁻⁵ K⁻¹)，体积模量B_T (kbar)，热容量C_V (kJ∙mol⁻¹∙K⁻¹)

虽然在零压下没有关于Rb_xC₆₀ (x = 3,4,6)热力学性质随温度变化的实验数据，但根据平均场近似方法仍能对三类掺杂材料性质的变化趋势进行合理的预测。表1中给出了在零压下的最近邻距离、线性热膨胀系数、体积模量以及等容热容量随温度的变化。计算得到Rb ₃C ₆₀的螺旋温度约为2860 K，而Rb ₄C ₆₀和Rb ₆C ₆的螺旋温度都高于4000 K。这表明后两者在高温下比Rb ₃C ₆₀更稳定。另外，从表1可以得到晶格常数和热膨胀系数都是温度的增函数，而体积模量和等容热容量都随温度的升高而减小。在接近螺旋温度时，Rb ₃C ₆₀热膨胀系数变得发散而体积模量趋于零。

5. 结论

基于自由体积理论和解析平均场方法对Rb_xC₆₀ (x = 3,4,6)的热力学性质进行了研究。通过拟合实验数据优化获得了双指数势函数的三组势参量，作出了Rb_xC₆₀ (x = 3,4,6)的三条势函数曲线。对Rb_xC₆₀ (x = 3,4,6)的热力学性质进行了计算和分析，结果表明运用该方法得到的结果与实验以及其它文献结论符合很好。本文所采用的方法不但物理意义清晰、计算方便，而且还能对Rb_xC₆₀ (x = 3,4,6)在高温和高压下的热力学性质的变化趋势进行合理预测。

基金项目

成都大学1315人才工程项目(2081915041)。