拉盖尔–高斯光束在小尺度流场内的气动光学效应

Aero-Optical Effect of Laguerre-Gaussian Vortex Beams through a Small-Scale Flow Field

摘要: 为研究拉盖尔–高斯(LG)光束在经过由微小凸起造成的流场后的气动光学效应，采用二阶紧致差分对抛物型的复振幅微分方程进行求解，并使用四阶龙格库塔沿光束路径积分。比较了具有不同拓扑荷数的LG光束以及高斯光束在不同马赫数、不同攻角、不同海拔下的Strehl比(SR)以及成像偏移。仿真结果表明，在同样流场中，LG光束的拓扑荷数越大，相位稳定性越好且均优于高斯光束，但振幅稳定性越差，当且仅当径向指数为0，拓扑荷数为1时LG光束优于高斯光束。

Abstract: To learn about the propagation characteristics of Laguerre-Gaussian (LG) vortex beams through the aero-optical environment formed by a micro-turret, the parabolic beam equations of complex amplitude were solved by second-order compact differences and Runge-Kutta integration was used for integral along the optical path. Strehl ratio (SR) and imaging displacement were calculated at different Mach numbers, different angles of attack, different altitudes and compared among Gaussian beam and LG beams with different topological charges. Simulations show that in the same flow field, the LG beam which has more topological charges, the phase of it has better stability and is always better than that of Gaussian beam, while the amplitude of it has worse stability, only when the radial mode index equals 0 and topological charge equals 1, the amplitude stability of LG beam is better than that of Gaussian beam.

1. 引言

涡旋光束因其特殊的螺旋形相位和自身携带的轨道角动量(OAM)自1989年由Cullet等人 [1] 提出后就引起了人们广泛的讨论 [2] [3] 。其中OAM可以用于提高光通信容量的特点 [4] ，使得众多学者开始研究涡旋光束在大气中的传播特性 [5] [6] 。然而在一些应用环境中，涡旋光束需要经过空气密度高频变化的气动区域，而涡旋光束在气动区域中的传输特性还鲜有研究中提及，因此对涡旋光束气动光学效应的研究是涡旋光束在光通讯领域内应用的进一步拓展。

目前在气动光学的研究中，例如Philip E. Morgan等人 [7] 采用沿着光束行进路径积分计算OPD的方式，对经过具有平型窗口凸台周围流场的光束的气动光学效应进行了探究；Gordeyev等人 [8] 通过搭建经过超音速流场的实验光路并以OPD为计算结果，研究了超音速流场中边界层处的气动光学效应；高穹等人 [9] 对光束经过超音速湍流边界层后光畸变的统计特性进行了探讨；John P Siegenthaler等人 [10] 研究了剪切层与孔径对气动光学效应的影响，以上对于气动光学效应的研究，除了被研究光源均为高斯光束以外，光场计算的方法也均为基于费马原理的光线追迹法。

由于其他含有OAM的光束在通信时理论上可以看作是具有不同径向指数和相同OAM的LG光束的线性叠加 [11] ，并且LG光束是涡旋光束中最为基本的一种涡旋光，因此本文将研究具有3种不同拓扑荷数的LG光束，分别在以攻角、海拔、速度作为流场唯一变化条件时，经过小尺度流场后的气动光学效应。在文中第2小节里所介绍的流场的气动模型和光场的传输模型中，光场的传输计算方法则有别于传统的光线追迹理论，介绍的是基于亥姆霍兹方程的数值仿真算法。第3小节介绍了LG光束和高斯光束在不同流场环境下经过远场衍射后的SR和成像偏移，第4小节总结了本文的工作并得出LG光束在小尺度流场内所表现出的气动光学效应规律性的结论以及与高斯光束有别的特性。

2. 理论分析

2.1. 气动模型

LG光束所经过的流场为一由微小凸起(以下简称凸起)造成的流场。凸起为一圆柱体加上半球体构成，置于一平面中心，即凸起底面圆心位置为(0,0)，如图1所示。截取凸起正上方2 × 2 × 1.73 mm³的流场作为光束要经过的小尺度流场。在LG光束传播1.73 mm后，可认为光束进入到折射率均匀的大气之中，一般而言，2 mm左右的传播距离已经能够使得光束表现出气动光学应。选用小尺度流场则是因为小尺度时流场的雷诺数较小，湍流激烈程度也较小，在流场仿真中更易形成稳定可收敛的流场。

采用Computational Fluid Dynamics (CFD)仿真时，设置飞行速度为0.6 Ma至4.6 Ma，飞行高度为6 Km至10 Km，攻角为0˚至20˚，流场仿真方法选用大涡模拟(LES)。

此处的攻角定义为来流与凸起横轴之间的夹角，光束沿着凸起的纵轴垂直出射，观察方向沿着光束出射方向的反方向。当来流为超音速时，凸起头部处会形成如图2所示的弓形激波。

Figure 1. Flow field parameters (in: mm)

图1. 流场尺寸示意图(单位：mm)

Figure 2. Contour of density

图2. 密度云图

2.2. 传输模型

在非均匀介质中，麦克斯韦方程可以简化为如下的亥姆霍兹方程：

${\nabla }^{2}U\left(r\right)+k^2{n}^2\left(r\right)U\left(r\right)=0$ 。 (1)

将光场复振幅 $U\left(r\right)$ 展开为抛物型表达式 $U\left(r\right)=A\left(x,y,z\right){\text{e}}^{ikz}$ 代入(1)式中，在满足旁轴近似 $\left|{\partial }_{zz}A\right|\ll \left|k{\partial }_{z}A\right|$ 时，(1)式可以演变为振幅A对传播方向z的隐式微分方程 [12] ：

$f\left(z,A\right)\approx \frac{i}{2k}{\nabla }_{\perp }^{2}A+\frac{ik}{2}\left[{\left(\frac{n}{n_r}\right)}^2-1\right]A$ ， (2)

式中 $f\left(z,A\right)=\frac{\partial A}{\partial z}$ ， $n_r$ 为自由空间折射率，采用二阶紧致差分方法计算振幅A横截面上的二阶偏导 ${\nabla }_{\perp }^{2}A=\frac{{\partial }^{2}A}{\partial x^2}+\frac{{\partial }^{2}A}{\partial y^2}$ ，再沿着积分路径也即光束行进路径，采用四阶龙格库塔积分即可得到目标距离处的光

振幅分布，并由此可以求解出目标距离处的OPD分布：

$\Delta =\frac{\lambda }{2\text{π}}\mathrm{Re}\left\{-iIn\frac{A^{n+1}}{A_r^{n+1}}\right\}$ ， (3)

式中 $A^{n+1}$ 、 $A_r^{n+1}$ 分别是光束在气动区域和自由空间中传播同等距离后的振幅分布。

光束出气动区域后，使用离散化的夫琅禾费衍射积分公式对远场光振幅进行计算：

$\tilde{E}\left(x,y\right)=\frac{1}{i\lambda z_0}\exp \left[ik\left(z_0+\frac{x^2+y^2}{2z_0}\right)\right]{\displaystyle \underset{j=1}{\overset{\frac{2a}{\Delta y_1}}{\sum }}{\displaystyle \underset{i=1}{\overset{\frac{2b}{\Delta x_1}}{\sum }}\exp \left[-ik\left(\frac{x}{z_0}{x}_1+\frac{y}{z_0}{y}_1\right)\right]A^{n+1}\left(x_1,y_1\right)\Delta x_1\Delta y_1}}$ ， (4)

式中 $z_0$ 为衍射距离，2a、2b分别为y、x两方向的衍射面长度。 $\Delta x_1=\Delta y_1=0.01$ ， $\Delta z=0.001$ 。

光束穿过小尺度流场后，其远场成像质量采用SR和成像位移两种参数分别从相位稳定性和相对于光信号接收器件而言的振幅稳定性两方面进行评价。SR通常采用的计算公式为 [12] ：

$\text{SR}=\exp \left[-{\left(k\cdot {\Delta }_{rms}\right)}^2\right]$ , (5)

其中 ${\Delta }_{rms}$ 为OPD的均方差。成像位移的计算公式为：

$\Delta \bar{r}=\bar{r}-{\bar{r}}_0$ , (6)

式中 $\bar{r}$ 、 ${\bar{r}}_0$ 分别为光束经过气动区域和未经过气动区域后远场衍射图中的光束质心位置。此处的振幅稳定性是相对于光信号接收器件而言。

以上对光场的传输计算和对评价参数的计算，采用的软件均为Mathematica。

3. 振幅和相位稳定性

采取攻角分别为0˚、5˚、10˚、15˚、20˚，海拔分别为6 Km、7 Km、8 Km、9 Km、10 Km，速度分别为0.6 Ma、1.6 Ma、2.6 Ma、3.6 Ma、4.6 Ma的条件进行仿真。采用径向指数p = 0，拓扑荷数l = 1、2、3的LG光束(为方便描述，分别简记为L1、L2、L3)以及高斯光束作为仿真对象，分别探究攻角、海拔、马赫数的变化对LG光束光强和OPD的影响。其中，高斯光束在初始面处的振幅分布如下：

$A\left(x,y,z\right)=\frac{\exp \left[-a_{0}k\frac{x^2+y^2}{2\left(1+i{a}_{0}z\right)}\right]}{1+i{a}_{0}z}$ , (7)

式中 $a_0=\frac{2}{1+k{\omega }_0^2}+\frac{i}{R_0}$ ， $R_0$ 为波前初始半径， ${\omega }_0$ 为光束初始束腰。LG光束在初始面上的分布为 [13] ：

$\begin{array}{c}A\left(x,y,z,p,l\right)=\sqrt{\frac{2p!}{\text{π}\left(\left|l\right|+p\right)!}}\cdot \frac{1}{\omega \left(z\right)}\cdot \exp \left[i\left(2p+\left|l\right|+1\right)\phi \left(z\right)\right]\cdot {\left[\frac{\sqrt{2\left(x^2+y^2\right)}}{\omega \left(z\right)}\right]}^{\left|l\right|}\\ \cdot L_p^{\left|l\right|}\left[\frac{2\left(x^2+y^2\right)}{{\omega }^2\left(z\right)}\right]\cdot \exp \left[-ik\frac{x^2+y^2}{2q\left(z\right)}+il\arctan \left(\frac{y}{x}\right)\right]\end{array}$ ， (8)

式中 $\omega \left(z\right)={\omega }_0\sqrt{1+Z_N^2}$ ， $Z_N=\frac{z}{Z_R}$ ， $Z_R=\frac{1}{2}k{\omega }_0^2$ ， $\phi \left(z\right)=\arctan \left(Z_N\right)$ ， $q\left(z\right)=z+i{Z}_R$

图3(a)~(d)、图3(e)~(h)分别为高斯光束和LG光束的初始光强分布和相位分布。

不同拓扑荷数的LG光束以及高斯光束经过气动区域后，不同大小的光斑会携带不同位置的OPD数值，这些OPD数值会体现在实部和虚部的变化当中，变化了的实部虚部会在远场衍射中进一步影响光强的分布，使其充分地显示出气动光学效应。因此在计算光束的SR和成像偏移之前，光场又先进行了夫琅禾费远场衍射计算。

3.1. 光束的相位稳定性

由(5)式可知，SR与光束的OPD均方差呈负相关关系，故使用SR来描述光束的相位稳定性。图4是高斯光束和L1、L2、L3光束的SR值随攻角变化的曲线图：

由图4可知，随着攻角的增大，各光束的SR均逐渐下降。对于LG光束而言，在同一攻角下，随着拓扑荷数的增加，SR也在增加，可见当攻角作为流场唯一变化条件时，拓扑荷数越大，光束的相位稳定性越好，并且LG光束的SR总是大于高斯光束的SR，故LG光束的相位稳定性高于高斯光束。此外，随着攻角的增大，不同光束间的SR差值在缩小，可见在大攻角的情况下，拓扑荷数对相位稳定性的影响不大，而在小攻角处，拓扑荷数大的LG光束具有明显的相位稳定优势。

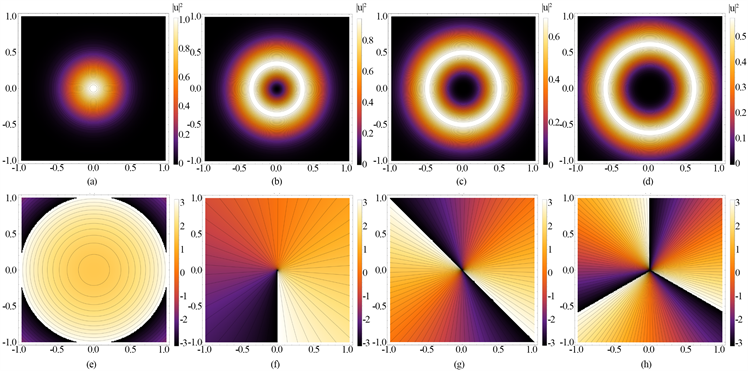
Figure 3. (a)~(d) Intensity, (e)~(h) Phase, (a, e) Gaussian beam, (b, f) L1, (c, g) L2, (d, h) L3

图3. (a)~(d)光强分布，(e)~(h)相位分布，(a, e)、(b, f)、(c, g)、(d, h)依次为高斯光束，L1、L2、L3

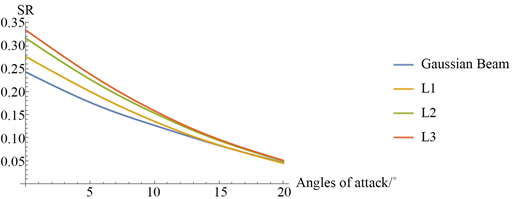
Figure 4. SR at different angles of attack

图4. SR随攻角变化曲线图

图5是高斯光束和L1、L2、L3光束的SR值在0˚攻角、2.6 Ma的飞行速度下，随海拔变化的曲线：

由图5可知，随着海拔的增大，各光束的SR值均在逐渐增大，各光束间SR的差值也在扩大，且LG光束的SR值依旧高于高斯光束。对于LG光束而言，在同一海拔下，随着拓扑荷数的增加，SR也在增加。所以在海拔作为流场唯一变化条件时，拓扑荷数越大，LG光束的相位稳定性越好，且相互之间的差距随着海拔的增大而扩大。

图6是在0˚攻角，10 Km飞行高度下，高斯光束和L1、L2、L3光束的SR值随马赫数的变化曲线：

由图6可知，在马赫数由亚音速增加到超音速之时，各光束的SR值都有一个大的跌落，但是对于L2和L3两束LG光束而言，当马赫数继续增加时，其SR值几乎维持不变，而L1光束与之相比，则依旧呈现出下降的趋势。可见当马赫数作为流场唯一变化条件时，LG光束的拓扑荷数越大，光束相位稳定性越好，且相互之间差距较大。当马赫数大于2 Ma时，马赫数对拓扑荷数大于1的LG光束相位稳定性的影响不大。

图6中显示，高斯光束于3.6 Ma处的SR值较其在2.6 Ma时的SR值略大，约在2 × 10⁻²，而于4.6 Ma又有所下降。该现象的可能原因是3.6 Ma下的仿真流场，在光束路径所经过的流场部分，较大的空气密度浮动与2.6 Ma相比处在所计算的截面较为外侧的区域，而相同束腰下高斯光束的光斑最小，所以于3.6 Ma处高斯光束的SR又略有上升。

就相位稳定性而言，LG光束的拓扑荷数越大，相位稳定性越好，且均优于高斯光束。其中拓扑荷数大于1的LG光束在经过高马赫数飞行产生的流场后其相位稳定的优势非常明显。当且仅当攻角作为流场唯一变化条件时，随着攻角的增加，LG光束间的相位稳定性差距在减小。

3.2. 光束的振幅稳定性

当海拔、马赫数、攻角分别作为流场唯一变量时，采用成像偏移(以下简称偏移)来查看气动光学效应对光束质心位置产生的影响。图7是高斯光束以及L1、L2、L3三种LG光束在10 Km、2.6 Ma飞行速度下偏移量随攻角增大而变化的曲线图：

由图7可以看出，随着攻角的增加，偏移也在逐渐增大。对于高斯光束和L1、L2两束LG光束而言，在攻角小于15˚的时候，偏移变化幅度很小，而当攻角大于15˚后，这三束光的偏移量均大大增加，可见对于这三束光，在一定的攻角范围内，均能较好的保持成像位置。并且我们发现L1光束的偏移量一直保持在高斯光束之下，可见其比高斯光束有着更好的振幅稳定性。而对于L3光束而言，随着攻角的增加，其偏移大幅增加。因此，对LG光束而言，拓扑荷数越大，其成像偏移越大，当拓扑荷数大于2时，振幅稳定性极差。在攻角为0˚至15˚的范围内时，对高斯光束和拓扑荷数小于3的LG光束而言，攻角变化对其偏移的影响并不明显。

Figure 5. SR at different altitudes

图5. SR随海拔变化曲线图

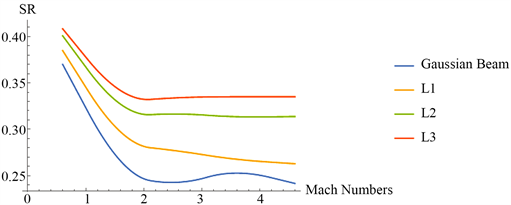
Figure 6. SR at different Mach Numbers

图6. SR随马赫数变化曲线图

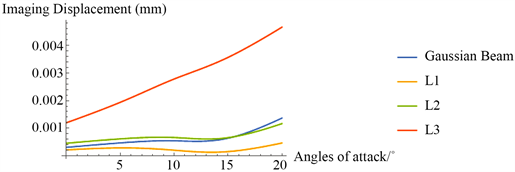
Figure 7. Imaging displacements at different angles of attack

图7. 成像偏移随着攻角的变化

图8是高斯光束以及L1、L2、L3三种LG光束在0˚攻角、2.6 Ma飞行速度下偏移量随海拔增加而变化的曲线图：

由图8可以看到，随着海拔的增加各光束的偏移量均呈现下降的趋势。L1、L2光束偏移量均明显小于L3，且三者之差越来越小。可见海拔越高，光束的振幅稳定性越好，虽然各光束之间的振幅稳定性差距随着海拔的增加而减小，但相互之间的差距仍然很大。

图9是高斯光束以及L1、L2、L3三种LG光束在0˚攻角、10 Km飞行高度下随马赫数的增大，偏移量的变化曲线图：

由图9可知，随着马赫数的增加，成像偏移量有增加有减少。与之前的规律相似，高斯光束和L1、L2两束LG光束的偏移量均明显小于L3光束，其中L1光束又小于高斯光束，并且在0.6 Ma、1.6 Ma处，L2的偏移量也小于高斯光束。对于高斯光束和L1、L2两束LG光束而言，在马赫数由亚音速升至

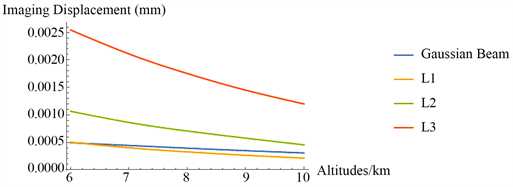
Figure 8. Imaging displacements at different altitudes

图8. 成像偏移随着海拔的变化

Figure 9. Imaging displacement at different Mach numbers

图9. 成像偏移与马赫数的关系

超音速的过程中，偏移量有个极大的增加。而在速度由1.6升至4.6 Ma的过程中，偏移量经历了下降、上升、下降的过程。对于L3光束而言，当速度从0.6 Ma升至3.6 Ma时，其偏移量一直在增加，只是增加的幅度不一样，但在4.6 Ma处，偏移量有所下降。该现象的可能原因是当马赫数较大时，激波进一步靠近头部，雷诺数也在增加，因此边界层变薄，故图像偏移量下降。所以在其它飞行条件不变时，各光束的振幅稳定性在马赫数大于音速后都有极大的降低，而当马赫数继续增加时，振幅稳定性则产生波动，没有稳定的走向。

就振幅稳定性而言，拓扑荷数越大，振幅稳定性越差，其中L3光束的振幅稳定性远远小于L1、L2光束，且仅有L1光束，其振幅稳定性总是优于高斯光束。在攻角为0˚到15˚时，攻角的变化对拓扑荷数小于3的LG光束的振幅稳定性没有明显影响。

4. 结论

采用LES对小尺度流场进行了仿真，得到了流场区域内的空气密度数据，再由旁轴近似的数值算法，仿真计算了不同拓扑荷数的LG光束在经过小尺度流场后，又经过2m远场衍射后的OPD和光强分布，并以SR和成像偏移对远场光束质量进行了评价。在对不同拓扑荷数的LG光束远场成像质量的比较中发现，LG光束的拓扑荷数越大，其穿过小尺度气动区域后的相位稳定性就越好，且总是优于高斯光束；在高马赫数时，拓扑荷数大的LG光束相位稳定的优势相当明显；当且仅当攻角作为小尺度流场唯一变化条件增大时，不同拓扑荷数的LG光束其相位稳定性的差距是在减小的。而拓扑荷数与振幅稳定性则呈现出负相关的关系，尤其是拓扑荷数大于2的LG光束，其振幅稳定性远远小于L1、L2光束，此时有且只有L1光束的振幅稳定性优于高斯光束，即L1光束无论在振幅稳定性还是相位稳定性方面，其在小尺度流场内的表现都优于高斯光束；当攻角在0˚到15˚之间变化时，拓扑荷数小于3的LG光束振幅稳定性几乎不受影响。

通过对不同拓扑荷数的LG光束与高斯光束经过小尺度流场后的远场成像质量的比较，对涡旋光束在气动环境下的气动光学效应探究提供了方法上的借鉴，对自由空间光通信技术在气动领域的扩展具有相当积极的引领作用。

基金项目

国家自然科学基金(61077012, 61107011, 61675098)。