1. 引言
本节中将给出一些基本的概念以及符号,方便后续使用。
设
为复平面,
为
中的单位开圆盘,使用dA定义D上的面积测度,所以规范D的面积是1,按照直角坐标和极坐标,有
,其中
。
定义1.1:设
表示D上所有勒贝格平方可积的函数构成的集合,定义内积
则
为一个Hilbert空间。
定义1.2:
中的全体解析函数构成了Bergman空间
。
定义1.3:我们设P为
到
的正交投影,众所周知
为
的闭子空间。则有
,其中
为Bergman空间的再生核。
定义1.4:调和Bergman空间
为D上所有调和函数构成的集合。
定义1.5:设Q表示
到
的正交投影,显然是为
的闭子空间。容易验证对任意的
,存在
中唯一一个函数
,使得
,
,通过计算可知
,因此有
.
定义1.6:设
为一个酉算子,定义为
,
.
定义1.7:设
,
是定义在
的乘法算子,即
。
定义1.8:
,以φ为符号的大Hankel算子定义为
。
定义1.9:若函数φ满足
,则称φ为径向函数。下文中将用
表示D上全体径向函数构成的集合。
本篇论文主要研究以调和函数φ为符号的大Hankel算子的一些性质, [1] 中给出了调和函数以及调和Bergman空间的一些结论, [2] 中给出了以调和函数φ为符号的Toeplitz算子的一些性质的结论, [3] 研究了正定性的一些结论,本文主要根据 [4] [5] 给出的大小Hankel算子的一些性质结论为研究前提,结合 [2] 中讨论的以调和函数φ为符号Toeplitz算子来研究以调和函数φ为符号的大Hankel算子的一些性质。
2. 主要结论
本文主要讨论以径向函数为符号的大Hankel算子的一些性质。
定理2.1:设函数
,函数
。
,令
,则有
。
证明:显然
因为
为径向函数,故当
时,
。
又因为
,
因此得到
。
引理2.1 [1] :设
,
,
,
;
,
,则 为
为 的正规正交基。
的正规正交基。
2.1. 大Hankel算子的有界性
定理2.2:设函数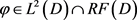 ,则
,则 有界当且仅当
有界当且仅当 有界。
有界。
证明:先证明必要性:假设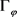 为有界线性算子。
为有界线性算子。
由引理2.1我们知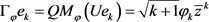 ,
,
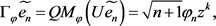
且 ,同理
,同理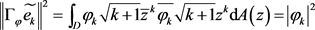 ,故有
,故有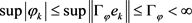 即
即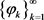 有界。
有界。
接下来证明充分性:假设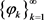 有界,且
有界,且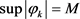 ,由定理2.1
,由定理2.1
设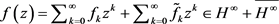
则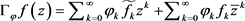
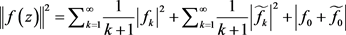
而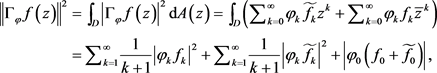
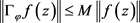
又因为 在
在 中稠密,故
中稠密,故 为有界算子。
为有界算子。
2.2. 大Hankel算子的紧性
定理2.3:设函数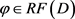 ,则有
,则有 为紧算子当且仅当
为紧算子当且仅当 ,
, 。
。
证明:先证明必要性:假设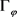 为紧算子,而正规正交基
为紧算子,而正规正交基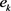 弱收敛于0,
弱收敛于0, ;且
;且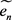 弱收敛于0,
弱收敛于0, 。因此有
。因此有 。
。
下面证明充分性: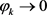 ,
,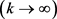 ,有
,有 为紧算子。
为紧算子。
若有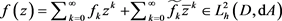 ,可以证明
,可以证明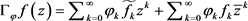 。
。
因为 在
在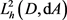 中稠密,因此存在序列
中稠密,因此存在序列 ,使
,使

因此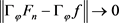 ,
,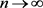 。由定理2.1我们知道
。由定理2.1我们知道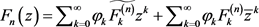
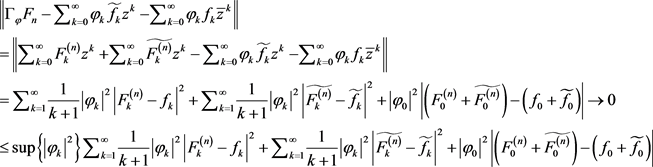
因此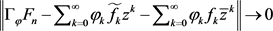 ,
,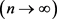 。
。
故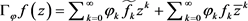 。
。
对于正整数K,定义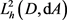 上算子,对
上算子,对 。
。
令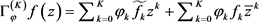 。
。
显然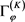 为一个有限秩算子,因此
为一个有限秩算子,因此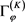 为一个紧算子。
为一个紧算子。
而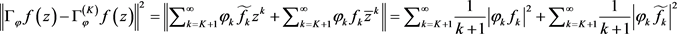 。
。
而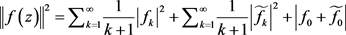 ,且
,且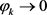 ,
, 时,故
时,故 ,
,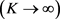 因此
因此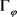 为紧算子。
为紧算子。
2.3. 大Hankel算子的正定性
定理2.4:设函数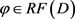 ,则
,则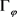 为正定的当且仅当
为正定的当且仅当 为正项数列,即
为正项数列,即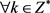 ,都有
,都有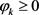 。
。
证明:先证明必要性:设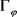 为正定的,由正定的定义我们知道,对于
为正定的,由正定的定义我们知道,对于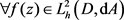 ,我们有
,我们有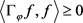 ;则对于
;则对于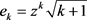 有
有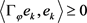 即
即 则一定有
则一定有 。
。
下面证明充分性: 为正项数列,即
为正项数列,即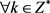 ,都有
,都有 ;
;
任意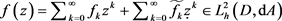 ,
,
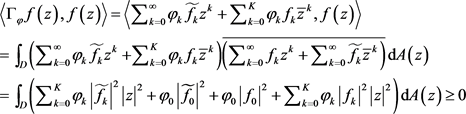
故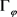 为正定。
为正定。