四维速度与四维力的正交性及其在教学中的应用

The Orthogonality of 4-Vector Velocity and 4-Vector Force and Its Applications in Teaching

摘要: 根据四维速度与四维力的正交性，推导出了四维空间中库仑力的相对论表达式，由此推导出了相对论Lorentz力，并详细讨论它与Maxwell方程组的关系；本文指出这些推导形成了一种分析Maxwell方程组的新方法。在电磁学和电动力学教学中，如果从四维速度与四维力正交性出发，能够更好地理解相对论与Maxwell方程组之间的关系。

Abstract: According to the orthogonality of 4-vector velocity and 4-vector force, the Coulomb force between two charged particles is expressed in terms of relativistic 4-vectors, from which the relativistic Lorentz force is derived, and Maxwell equations are discussed in detail; it was pointed out that these derivations form a new method for analyzing the Maxwell equations. In the teaching of elec-tromagnetics and electrodynamics, the orthogonality of 4-vector velocity and 4-vector force pro-vides useful insights into the relationship of the relativity and the Maxwell equations.

1. 引言

在相对论中，一个粒子的四维速度u与它受到的四维力f之间具有正交性 [1]

$f_{\mu }{u}_{\mu }=0$ (1)

这里下标 $\mu =1,2,3,4$ ，重复的下标代表求和(爱因斯坦求和约定)。这个正交性是由于四维速度的模 $\left|u\right|$ 是一个常量所致，即

$u_{\mu }{u}_{\mu }=-c^2\text{or}\left|u\right|=ic$ (2)

任何力都不能改变四维速度的模 $\left|u\right|$ 而只能改变四维速度的方向 [2] [3] 。

一个粒子的四维速度u与它受到的四维力f正交，那么在电磁学和电动力学中这个粒子的经典速度矢量 $v$ 与它受到的经典力 $$ 矢量是否会正交或垂直？那么，从相对论四维空间变换到我们比较熟悉的三维空间， $\left(u,f\right)\Rightarrow \left(v,f\right)$ ，力的方向是如何变换的呢？这些问题没有一个简单的答案，也没有文献专门讨论这个问题。所以，本文有必要详细讨论四维空间中力的方向问题。

2. 四维空间中力的方向

在相对论四维空间 $\left(x_1,x_2,x_3,x_4=ict\right)$ 中，考虑两个带电粒子q和 $q^{\prime }$ ，它们之间的电磁相互作用四维力为f；这两个粒子的位置在x和 $x^{\prime }$ ，它们的四维速度为u和 $u^{\prime }$ ，用m代表粒子q的质量。显然，粒子q是在粒子 $q^{\prime }$ 产生的电场 $E$ 和磁场 $B$ 中运动。如图1所示，注意，图中用欧几里得矢量垂直表示了四维空间 $\left(x_1,x_2,x_3,x_4=ict\right)$ 的矢量正交，以显示正交的直观性。

在四维力f在R和 $u^{\prime }$ 构成的平面内，我们假定可以把四维力f的表达式写成

$f=CR+D{u}^{\prime }$ (3)

R和 $u^{\prime }$ 是我们选择的两个基矢，如图1所示，要求 $R\cdot u^{\prime }=0$ 是为了后面讨论的方便，并且定义 $r=\left|R\right|$ 。C和D是相对于这两个基矢的展开系数。使用四维速度u与四维力f的正交性，我们有

$u\cdot f=C\left(u\cdot R\right)+D\left(u\cdot u^{\prime }\right)=0$ (4)

消去系数C，方程(3)变成

$f=\frac{D}{\left(u\cdot R\right)}\left[-\left(u\cdot u^{\prime }\right)R+\left(u\cdot R\right)u^{\prime }\right]$ (5)

这样，四维速度u与四维力f的正交性就决定了四维力f的方向。四维力f方向的单位矢量 $f^0$ 是

Figure 1. The particle positions, the orthogonality of 4-vector velocity and 4-vector force in the four dimensional space-time

图1. 四维空间中的两个粒子的相对位置，四维速度与四维力正交(图中用“垂直”来代表“正交”)

$f^0=\frac{1}{c^{2}r}\left[-\left(u\cdot u^{\prime }\right)R+\left(u\cdot R\right)u^{\prime }\right]$ (6)

设四维速度u与 $u^{\prime }$ 之间的夹角为 $\alpha$ ，很容易验算如下：

$f^0=\frac{1}{c^{2}r}\left[-\left(\left|u\right|\left|u^{\prime }\right|\cosh \alpha \right)R+\left(\left|u\right|\left|R\right|\sinh \alpha \right)u^{\prime }\right]$ (7)

$f^0\cdot f^0={\cosh }^2\alpha +{\sinh }^2\alpha =1$ (8)

知道了四维力f方向的单位矢量，那么这两个粒子之间的电磁相互作用的四维力f的一般表达式为

$f=\left|f\right|f^0=\left|f\right|\frac{1}{c^{2}r}\left[-\left(u\cdot u^{\prime }\right)R+\left(u\cdot R\right)u^{\prime }\right]$ (9)

3. 四维空间中库仑力的方向

现在具体讨论这两个粒子之间的库仑力，假设库仑力的大小就是四维力f的模

$\left|f\right|=\frac{kq{q}^{\prime }}{r^2}$ (10)

那么，四维空间中库仑力的表达式为

$\begin{array}{c}f=\left|f\right|f^0=\frac{kq{q}^{\prime }}{c^2{r}^3}\left[-\left(u\cdot u^{\prime }\right)R+\left(u\cdot R\right)u^{\prime }\right]\\ =q\left[-\left(u\cdot \frac{k{q}^{\prime }{u}^{\prime }}{c^2{r}^3}\right)R+\left(u\cdot \frac{k{q}^{\prime }R}{c^2{r}^3}\right)u^{\prime }\right]\end{array}$ (11)

$f_{\mu }=q\left[-\left(u_{\nu }\frac{k{q}^{\prime }{u^{\prime }}_{\nu }}{c^2{r}^3}\right)R_{\mu }+\left(u_{\nu }\frac{k{q}^{\prime }{R}_{\nu }}{c^2{r}^3}\right){u^{\prime }}_{\mu }\right]$ (12)

利用电动力学中的一个常用公式

$\frac{\partial }{\partial x_{\mu }}\left(\frac{1}{r}\right)=-\frac{R_{\mu }}{r^3}$ (13)

方程(12)可以写成

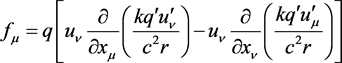(14)

根据电动力学中的常用书写格式，把方程(14)的四维库仑力f的公式整理成为

$f_{\mu }=q{F}_{\mu \nu }{u}_{\nu };F_{\mu \nu }=\frac{\partial A_{\nu }}{\partial x_{\mu }}-\frac{\partial A_{\mu }}{\partial x_{\nu }};A_{\mu }=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^{2}r}$ (15)

这样我们就对四维库仑力f有了一个熟悉而又直观的认识：A是粒子 $q^{\prime }$ 产生的四维电磁矢势；四维库仑力与相对论Lorentz力 $f_{\mu }=q{F}_{\mu \nu }{u}_{\nu }$ 在形式上保持一致；在四维空间中可以从库仑力推导出相对论的Lorentz力。

4. 四维空间中的Maxwell方程组

就这两个粒子而言，我们在选择基矢R的时候，要求 $R\cdot u^{\prime }=0$ ，即它们正交，并且定义 $r=\left|R\right|$ 。如图1所示，我们有

${u^{\prime }}_{\mu }{R}_{\mu }=0$ (16)

所以

$\frac{\partial A_{\mu }}{\partial x_{\mu }}=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^2}\frac{\partial }{\partial x_{\mu }}\left(\frac{1}{r}\right)=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^2}\left(\frac{-R_{\mu }}{r^3}\right)=0$ (17)

我们知道，方程(17)就是Lorentz规范条件(Lorentz gauge condition)。而我们又知道数学公式

$$ (18)

这样，我们就计算出

$\begin{array}{c}\frac{\partial F_{\mu \nu }}{\partial x_v}=\frac{\partial }{\partial x_{\nu }}\frac{\partial A_{\nu }}{\partial x_{\mu }}-\frac{\partial }{\partial x_{\nu }}\frac{\partial A_{\mu }}{\partial x_{\nu }}=-\frac{\partial }{\partial x_{\nu }}\frac{\partial A_{\mu }}{\partial x_{\nu }}\\ =-\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^2}\frac{\partial }{\partial x_{\nu }}\frac{\partial }{\partial x_{\nu }}\left(\frac{1}{r}\right)=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^2}4\text{π}\delta \left(r\right)\end{array}$ (19)

这里定义 ${J^{\prime }}_{\mu }=q^{\prime }{u^{\prime }}_{\mu }\delta \left(r\right)$ 作为粒子 $q^{\prime }$ 的电流密度矢量，也就是说

$\frac{\partial F_{\mu \nu }}{\partial x_{\nu }}={\mu }_0{J^{\prime }}_{\mu }$ (20)

把方程(15)中的 $F_{\mu \nu }$ 代入下式，交换下标并求和，就得到

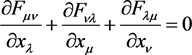(21)

方程(20)和方程(21)构成了Maxwell方程组。

把上面讨论的两个粒子模型应用到连续介质中去。如图2所示，粒子q是在附近电路产生的电场 $E$ 和磁场 $B$ 中运动。作用在粒子q上的四维电磁矢势A包含电路中所有载流子的贡献，它们是线性叠加的，有

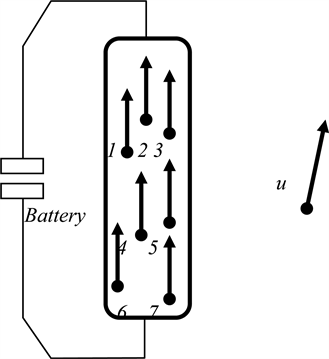
Figure 2. The electromagnetic 4-vector potential near a circuit where the Maxwell equations hold

图2. 一个电路在其附近产生四维电磁矢势，而Maxwell方程组仍然成立

$A_{\mu }={\displaystyle {\sum }_i\frac{k{q}^{\prime }{u^{\prime }}_{i\mu }}{c^2{r}_i}}$ (22)

那么，在这个电路附近，使用方程(22)，Maxwell方程组仍然成立

$\frac{\partial F_{\mu \nu }}{\partial x_{\nu }}={\mu }_0{J^{\prime }}_{\mu }$ (23)

$\frac{\partial F_{\mu \nu }}{\partial x_{\lambda }}+\frac{\partial F_{\nu \lambda }}{\partial x_{\mu }}+\frac{\partial F_{\lambda \mu }}{\partial x_{\nu }}=0$ (24)

在这一小节，我们证明了，四维速度u与四维力f的正交性与Maxwell方程组之间存在内在联系。可见，四维力方向涉及到电磁场理论的全局，在确定四维力方向的时候绝对不能出错。这是一种分析Maxwell方程组的新方法。

5. 教学应用：四维空间中的Lienard-Wiechert势

从Maxwell方程组我们知道，在图1中的两个粒子之间，电磁相互作用从粒子 $q^{\prime }$ 传播到粒子q需要一个延迟时间 $\Delta t$ ，我们把两个粒子的模型重新画在图3中。

在图3中，这个延迟时间 $\Delta t$ ，对应着从 $u^{\prime }$ 与R相交点出发沿R方向到达q点的距离，图3中上边的那段虚线指示这段距离，这段距离通过下式计算出

$r=c\Delta t$ (25)

这个延迟时间 $\Delta t$ ，也对应着从 $q^{\prime }$ 出发沿 $u^{\prime }$ 方向到达与R相交之点的距离，图3中左边的那段虚线指示这段距离。把 $\left({x^{\prime }}_{\nu }-x_{\nu }\right)$ 投影到 $u^{\prime }$ 的模 $\left|u\right|=ic$ 方向上(注意，这个模是虚数)，通过下式计算出这段距离

$ic\Delta t=\left(\frac{u^{\prime }}{ic}\right)\cdot \left(x^{\prime }-x\right)=\frac{1}{ic}{u^{\prime }}_{\nu }\left({x^{\prime }}_{\nu }-x_{\nu }\right)$ (26)

所以，把式(26)代入式(25)，我们有

$r=c\Delta t=\frac{1}{c}{u^{\prime }}_{\nu }\left({x^{\prime }}_{\nu }-x_{\nu }\right)$ (27)

A是粒子 $q^{\prime }$ 产生的四维电磁矢势，从新写成

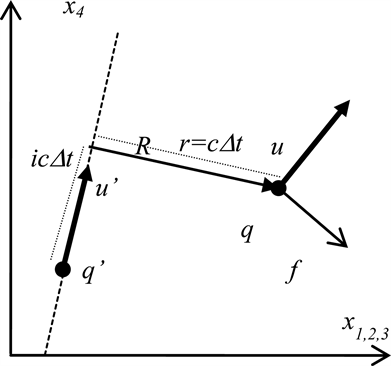
Figure 3. The particle positions in the four dimensional space-time

图3. 四维空间中的两个粒子的相对位置

$A_{\mu }=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c^{2}r}=\frac{k{q}^{\prime }{u^{\prime }}_{\mu }}{c{u^{\prime }}_{\nu }\left({x^{\prime }}_{\nu }-x_{\nu }\right)}$ (28)

这就Lienard-Wiechert势，它包含了延迟时间 $\Delta t$ (retardation time)。当初我们在选定基矢R的时候要求 $R\cdot u^{\prime }=0$ ，显然是考虑到这里的延迟时间 $\Delta t$ 机制，说明我们选择的基矢是合理的和自洽的。

6. 教学应用：从四维空间变换到我们比较熟悉的三维空间

从相对论四维空间变换到我们比较熟悉的三维空间，力的方向是如何变换的呢？我们下面给出的变换步骤可以帮助看清这一点。

第一步，四维电磁矢势A要用电场E和磁场B表示。

$F_{\mu \nu }=\left[\begin{array}{cccc}0& B_3& -B_2& -i{E}_1\\ -B_3& 0& B_1& -i{E}_2\\ B_2& -B_1& 0& -i{E}_3\\ i{E}_1& i{E}_2& i{E}_3& 0\end{array}\right]$ (29)

第二步，这样，力就可以写成Lorentz力的形式。

$f=qE+qv\times B;f_4=qE\cdot u$ (30)

四维力的第四分量表示电场对粒子q做功的功率。可见，一个粒子的四维速度u与它受到的四维力f正交，并不意味着在电磁学和电动力学中这个粒子的经典速度矢量v与它受到的经典力f矢量正交或垂直。但是四维速度与四维力的正交性具有丰富的内涵，这是本文讨论的重点。

第三步，Maxwell方程组，即方程(20)和方程(21)，要用电场E和磁场B表示，参见教材 [1] [4] [5] 。这样，我们就从相对论四维空间变换到我们比较熟悉的三维空间，以及得到我们比较熟悉的经典电磁学Maxwell方程组 [1] [4] [5] ：

$\begin{array}{l}\nabla \times B={\mu }_0\left(\rho v+{\epsilon }_0\frac{\partial E}{\partial t}\right),\nabla \cdot E=\frac{\rho }{{\epsilon }_0}\\ \nabla \times E=-\frac{\partial B}{\partial t},\nabla \cdot B=0\end{array}$ (31)

总之，在电磁学和电动力学教学中，如果从四维速度与四维力正交性出发，能够更好地理解相对论与Maxwell方程组之间的关系。

7. 结论

本文详细讨论四维空间中力的方向问题。根据四维速度与四维力的正交性，推导出了四维空间中库仑力的相对论表达式，由此推导出了相对论Lorentz力，并详细讨论它与Maxwell方程组的关系；本文指出这些推导形成了一种分析Maxwell方程组的新方法。在电磁学和电动力学教学中，如果从四维速度与四维力正交性出发，能够更好地理解相对论与Maxwell方程组之间的关系。

参考文献