一类捕食系统中的Hopf分岔

Hopf Bifurcation in a Class of Predator-Prey Systems

摘要: 本文研究了食饵具有防御机制的一类捕食系统。通过计算Lyapunov系数证明内部平衡点为一阶细焦点, 并给出了Hopf分岔的参数条件。

Abstract: In this paper, we studied a class of predator-prey system with a defense mechanism of the prey. By calculating the Lyapunov coefficient, the internal equilibrium point is proved to be a first order weak focus, and the parameter conditions of Hopf bifurcation are given.

1. 引言

Ajraldi [1] 研究了如下的食饵具有牧群行为的广义Holling-II功能函数反应

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{n}\right)-\frac{\alpha \sqrt{x}y}{1+t_h\alpha \sqrt{x}},\\ \frac{\text{d}y}{\text{d}t}=-sy+\frac{c\alpha \sqrt{x}y}{1+t_h\alpha \sqrt{x}}.\end{array}$

Braza [2] 研究了简化的食饵含有二次根号防御机制的函数反应

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\sqrt{x}y,\\ \frac{\text{d}y}{\text{d}t}=-sy+c\sqrt{x}y,\end{array}$

给出了内部平衡定的稳定性分析，在给出Hopf分岔分析时，并未计算Lyapunov系数，所以并不清楚在Hopf临界值时细焦点的阶数。

本文在上述研究成果的基础上，研究了一类食饵具有三次根号防御机制的函数反应

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\sqrt[3]{x}y,\\ \frac{\text{d}y}{\text{d}t}=-sy+c\sqrt[3]{x}y.\end{array}$ (1)

给出了内部平衡点的稳定性分析，并在判断Hopf分岔时给出了Lyapunov系数的值，计算出平衡点的类型为一阶稳定细焦点，改变参数后系统会发生Hopf分岔，平衡点的稳定性改变，分岔出一个稳定的极限环(参考 [3] [4] [5] )。

2. 主要结果

方程(1)的内部平衡点为 $E\left(x^{*},y^{*}\right)=\left({\left(\frac{s}{c}\right)}^3,\frac{s^2}{c^2}\left(1-\frac{s^3}{c^3}\right)\right)$ ，其Jacobian矩阵为

$J\left(x,y\right)=\left[\begin{array}{cc}1-2x-\frac{1}{3}{x}^{-\frac{2}{3}}y& -x^{\frac{1}{3}}\\ \frac{1}{3}c{x}^{-\frac{2}{3}}y& -s+c{x}^{\frac{1}{3}}\end{array}\right].$ (2)

定理2.1 假设 $s<s_0={\left(\frac{2}{5}\right)}^{\frac{1}{3}}c$ ，即为 $x^{*}<\frac{1}{3}$ ，则系统(1)在 $R_{+}^2$ 有一个从平衡点E经过

Hopf分岔出的稳定的极限环。

证明 由(2)，可得

$J\left(E\left(x^{*},y^{*}\right)\right)=\left[\begin{array}{cc}\frac{2c^3-5s^3}{3c^3}& -\frac{s}{c}\\ \frac{c^3-s^3}{3c^2}& 0\end{array}\right].$ (3)

令 $\sigma \left(s\right)=trJ\left(E\left(x^{*},y^{*}\right)\right),\Delta \left(s\right)=\det J\left(E\left(x^{*},y^{*}\right)\right),\mu \left(s\right)=\frac{1}{2}\sigma \left(s\right),\omega \left(s\right)=\frac{1}{2}\sqrt{4\Delta \left(s\right)-{\sigma }^2\left(s\right)}$ 。

由(3)，可得

$\mu \left(s\right)=\frac{1}{2}\sigma \left(s\right)=\frac{2c^3-5s^3}{6c^3},$

当 $s_0={\left(\frac{2}{5}\right)}^{\frac{1}{3}}c$ 时， $\mu \left(s_0\right)=0$ ，可得

$\omega \left(s_0\right)=\sqrt{\frac{c}{5}\times {\left(\frac{2}{5}\right)}^{\frac{1}{3}}}>0.$

我们可以检验如下横截条件

${\mu }^{\prime }\left(s_0\right)=-\frac{5}{2c}\times {\left(\frac{2}{5}\right)}^{\frac{2}{3}}<0.$

在 $s=s_0$ 时，平衡点 $E\left(x^{*},y^{*}\right)$ 的坐标为

$E\left(x^{*},y^{*}\right)=\left(\frac{2}{5},\frac{3}{5}\times {\left(\frac{2}{5}\right)}^{\frac{2}{3}}\right).$

为了把平衡点坐标移到原点 $\left(0,0\right)$ ，我们作平移变换

$\begin{array}{l}x=\frac{2}{5}+{\xi }_1,\\ y=\frac{3}{5}\times {\left(\frac{2}{5}\right)}^{\frac{2}{3}}+{\xi }_2.\end{array}$

则系统(1)变换为

$\begin{array}{l}{{\xi }^{\prime }}_1=-{\left(\frac{2}{5}\right)}^{\frac{1}{3}}{\xi }_2-\frac{5}{6}{\xi }_1{}^2-\frac{1}{3}\times {\left(\frac{2}{5}\right)}^{-\frac{2}{3}}{\xi }_1{\xi }_2-\frac{25}{108}{\xi }_1{}^3+\frac{1}{9}{\left(\frac{2}{5}\right)}^{-\frac{5}{3}}{\xi }_1{}^2{\xi }_2+o\left({\left|{\xi }_1,{\xi }_2\right|}^4\right),\\ {{\xi }^{\prime }}_2=\frac{c}{5}{\xi }_1-\frac{c}{6}{\xi }_1{}^2+\frac{c}{3}\times {\left(\frac{2}{5}\right)}^{-\frac{2}{3}}{\xi }_1{\xi }_2+\frac{25c}{108}{\xi }_1{}^3-\frac{c}{9}\times {\left(\frac{2}{5}\right)}^{-\frac{5}{3}}{\xi }_1{}^2{\xi }_2+o\left({\left|{\xi }_1,{\xi }_2\right|}^4\right).\end{array}$ (4)

我们可以把系统(4)写成如下形式

${\xi }^{\prime }=A\xi +\frac{1}{2}B\left(\xi ,\xi \right)+\frac{1}{6}C\left(\xi ,\xi ,\xi \right),$

其中B，C为向量函数，令 $\xi ={\left({\xi }_1,{\xi }_2\right)}^{\text{T}},\eta ={\left({\eta }_1,{\eta }_2\right)}^{\text{T}},\delta ={\left({\delta }_1,{\delta }_2\right)}^{\text{T}}$ ，则由(4)，可得

$B\left(\xi ,\eta \right)=\left(\begin{array}{c}-\frac{5}{3}{\xi }_1{\eta }_1-\frac{1}{3}{\left(\frac{2}{5}\right)}^{-\frac{2}{3}}\left({\xi }_1{\eta }_2+{\xi }_2{\eta }_1\right)\\ -\frac{c}{3}{\xi }_1{\eta }_1+\frac{c}{3}{\left(\frac{2}{5}\right)}^{-\frac{2}{3}}\left({\xi }_1{\eta }_2+{\xi }_2{\eta }_1\right)\end{array}\right),$ (5)

$C\left(\xi ,\eta ,\delta \right)=\left(\begin{array}{c}-\frac{25}{16}{\xi }_1{\eta }_1{\delta }_1+\frac{2}{9}{\left(\frac{2}{5}\right)}^{-\frac{5}{3}}\left({\xi }_1{\eta }_1{\delta }_2+{\xi }_1{\eta }_2{\delta }_1+{\xi }_2{\eta }_1{\delta }_1\right)\\ -\frac{25}{16}{\xi }_1{\eta }_1{\delta }_1-\frac{2c}{9}{\left(\frac{2}{5}\right)}^{-\frac{5}{3}}\left({\xi }_1{\eta }_1{\delta }_2+{\xi }_1{\eta }_2{\delta }_1+{\xi }_2{\eta }_1{\delta }_1\right)\end{array}\right)$ (6)

其中 $A=J\left(E\left(s_0\right)\right)$ ，即为

$A=\left(\begin{array}{cc}0& -{\left(\frac{2}{5}\right)}^{\frac{1}{3}}\\ \frac{c}{5}& 0\end{array}\right)=\left(\begin{array}{cc}0& -{\left(\frac{2}{5}\right)}^{\frac{1}{3}}\\ {\omega }^2{\left(\frac{5}{2}\right)}^{\frac{1}{3}}& 0\end{array}\right),$ (7)

其中 ${\omega }^2={\omega }^2\left(s_0\right)=\frac{c}{5}\times {\left(\frac{2}{5}\right)}^{\frac{1}{3}}$ 。

方程 $Aq=i\omega q,A^{\text{T}}p=-i\omega p$ 的复特征向量为

$q=\left(\begin{array}{c}{2}^{\frac{1}{3}}\\ -i\omega 5^{\frac{1}{3}}\end{array}\right),p=\frac{1}{2\omega 5^{\frac{1}{3}}{2}^{\frac{1}{3}}}\left(\begin{array}{c}{5}^{\frac{1}{3}}\omega \\ -i{2}^{\frac{1}{3}}\end{array}\right),$ (8)

且 $\langle p,q\rangle =1$ 。由(5)，(6)，(8)可得

$B\left(q,q\right)=\left(\begin{array}{c}-\frac{5}{3}\times 2^{\frac{2}{3}}+\frac{5i\omega }{3}\times 2^{\frac{2}{3}}\\ -\frac{c}{3}\times 2^{\frac{2}{3}}-\frac{5ci\omega }{3}\times 2^{\frac{2}{3}}\end{array}\right),B\left(q,\bar{q}\right)=\left(\begin{array}{c}-\frac{5}{3}\times 2^{\frac{2}{3}}\\ -\frac{c}{3}\times 2^{\frac{2}{3}}\end{array}\right),$ (9)

且

$C\left(q,q,\bar{q}\right)=\left(\begin{array}{c}-\frac{25}{9}-\frac{25i\omega }{9}\\ -\frac{25c}{9}+\frac{25ciw}{9}\end{array}\right).$ (10)

由(8)，(9)，(10)，可得

$\begin{array}{l}{g}_{20}=\langle p,B\left(q,q\right)\rangle =-\frac{5}{3}\times 2^{-\frac{2}{3}}+\frac{5i\omega }{3}-\frac{\frac{ic}{3}\times 2^{-\frac{1}{3}}}{5^{\frac{1}{3}}\omega }+\frac{5^{\frac{2}{3}}\times 2^{\frac{1}{3}}c}{3},\\ g_{11}=-\frac{5}{3}\times 2^{-\frac{2}{3}}-\frac{\frac{ic}{3}\times 2^{-\frac{1}{3}}}{5^{\frac{1}{3}}\omega },g_{21}=-\frac{27}{16}-\frac{27}{8}i\omega +\frac{9\sqrt{3}ci}{16\omega }-\frac{9\sqrt{3}c}{8}.\end{array}$

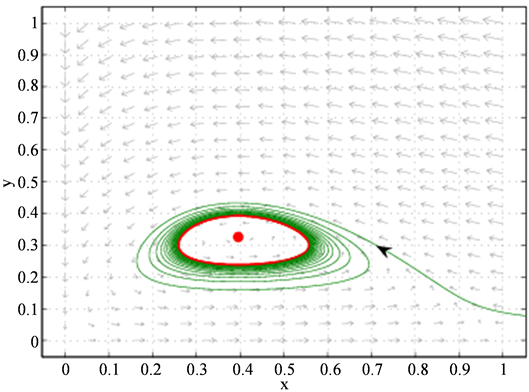
Figure 1. Stable limit cycle phase diagram of bifurcation from equilibrium point, bifurcation parameter is $s=0.734,c=1$

图1. 从平衡点 $E\left(x^{*},y^{*}\right)$ 分岔出的稳定的极限环相图，其中分岔参数为 $s=0.734,c=1$

我们可以计算参数在 $s=s_0={\left(\frac{2}{5}\right)}^{\frac{1}{3}}c$ 时的平衡点E的第一Lyapunov系数为

$l_1\left(s_0\right)=\frac{1}{2{\omega }^2}\mathrm{Re}\left(i{g}_{20}{g}_{11}+\omega g_{21}\right)=-\frac{5^{\frac{2}{3}}c}{18{\omega }^3}<0,$

则 $E\left(s_0\right)$ 为一阶细焦点，所以，当 $s<s_0$ 时，从平衡点 $E\left(x^{*},y^{*}\right)$ 分岔出一个稳定的极限环，参看图1。

基金项目

国家自然科学基金项目(11561019)；中央高校基本科研业务费专项资金资助(2012017yjsy141)。