大地电磁倾子响应的异常规律及影响分析

The Characteristics and Effects of Anomalous Body on Magnetotelluric Tripper Responses

摘要: 在二维地电模型中，大地电磁测深的倾子响应依赖于TE极化模式的数值模拟问题，能很好地反映地电构造的水平非均匀性，可作为复杂构造的表征。低阻覆盖层对电磁波具有屏蔽效应，会降低大地电磁测深的探测能力。通过对存在低阻覆盖层模型与不存在低阻覆盖层模型进行了正演计算，低阻覆盖层对于定性分析大地电磁的倾子响应资料是不存在影响的，而对于定性分析视电阻率资料的影响较大。同时，对静位移模型的模拟计算，倾子响应的实部、虚部和振幅均能反映出不均匀体的横向分布情况，且能分辨出地表不均匀体的横向不均匀性。

Abstract: In the two-dimensional geo-electric model, the tipper responses of magnetotelluric (MT) depend on the numerical simulation of the TE mode, which can reflect the horizontal distribution of the body and can provide for qualitative interpretation of field data. Because of the shielding effect on electromagnetic waves, the low-resistivity cover can reduce the detability of magnetotelluric sounding method. The low hindrance cover model and the model without low resistance cover are calculated, and the low resistance cover layer has no influence on the qualitative analysis of the magnetotelluric response data, but it has a great influence on the qualitative analysis of the ap-parent resistivity data. At the same time, for the simulation calculation of the static displacement model, the lateral distribution of the inhomogeneous body can be reflected by the real part, the imaginary part and the amplitude of the tilting response, and the lateral in-homogeneity of the surface inhomogeneous body can be distinguished.

1. 引言

大地电磁(Magnetotelluric，简称MT)是以天然电磁场为场源，通过在地表观测相互正交的电磁场分量来研究地球内部电性结构的一种重要的地球物理手段。大地电磁场具有很大的能量和极宽的频带范围，可以穿过巨厚的岩石圈，能为研究几十公里乃至数百公里深的地壳与上地幔提供信息 [1] 。大地电磁场的频带很宽，根据趋肤效应的原理，对应的探测深度的范围就很大，用它可以解决较多的地质问题，如大尺度地质单元的电磁感应研究、深部地壳地幔电性结构研究及壳幔中高导层的检测、油气资源普查、地热资源勘查、天然地震活动前兆监测以及地下水资源勘查和环境保护等 [2] [3] [4] [5] 。

大地电磁观测资料可以提供20多个参数供地质解释之用，但目前用于定性解释与定量解释的主要参数是视电阻率和阻抗相位，迫切需要借助其它参数来研究地下构造 [6] 。倾子响应能很好地反映地电构造的水平非均匀性，可作为复杂构造的表征，因此在构造解释中可以起到十分重要的作用 [7] [8] [9] 。因此，开展大地电磁倾子响应的异常规律特点及影响分析，有着重要的理论意义与实际意义。

2. 大地电磁倾子响应计算

在二维、三维地电模型中,磁场垂直分量 $H_z\ne 0$ ， $H_z$ 与两个磁场水平分量 $H_x$ 和 $H_y$ 之间存在如下的复系数线性关系 [10] ：

$H_z=T_{zx}{H}_x+T_{zy}{H}_y=\left[T_{zx},T_{zy}\right]\left[\begin{array}{l}{H}_x\\ H_y\end{array}\right]$ (1)

其中 $T=\left[T_{zx},T_{zy}\right]$ ，称为倾子响应，也叫做地磁转换函数。

假定地下电性结构是二维的，取走向为x轴正向，y轴与x轴垂直，保持水平，z轴垂直向下。根据谐变场的Maxwell方程组，可以导出两组独立的电磁场分量，称它们为TE极化模式和TM极化模式。

TE极化模式：

$\{\begin{array}{l}\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}=\sigma E_x\\ H_y=\frac{1}{\text{i}\omega \mu }\frac{\partial E_x}{\partial z}\\ H_z=-\frac{1}{\text{i}\omega \mu }\frac{\partial E_x}{\partial y}\end{array}$ (2)

TM极化模式：

$\{\begin{array}{l}\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}=\text{i}\omega \mu H_x\\ E_y=\frac{1}{\sigma }\frac{\partial H_x}{\partial z}\\ E_z=-\frac{1}{\sigma }\frac{\partial H_x}{\partial y}\end{array}$ (3)

式中 $\omega$ 为角频率， $\sigma$ 和 $\mu$ 为介质的电导率和磁导率。

从式(2)和式(3)可知： $H_z$ 只存在于TE极化模式中。因此，二维地电模型的倾子响应依赖于TE极化模式下的电磁场求解，从而有

$T_{zy}=\frac{H_y}{H_z}=-\frac{\frac{\partial E_x}{\partial z}}{\frac{\partial E_x}{\partial y}}$ (4)

在二维地电模型中，电场 $E_x$ 满足的偏微分方程为

$\frac{{\partial }^2{E}_x}{\partial y^2}+\frac{{\partial }^2{E}_x}{\partial z^2}+\text{i}\omega \mu \sigma E_x=0$ (5)

为了求解亥姆霍兹方程(5)，我们还必须给出相应的边界条件，如图1所示。

考虑到二维大地电磁倾子响应只依赖于TE极化模式的正演计算，我们这里给出TE极化模式的边界条件：

1) 上边界 $z=z_{\min }$ 离地面足够远，使异常场在 $z_{\min }$ 上为零，以该处的 $E_x$ 为1单位

${E_x|}_{z=z_{\min }}=1$ (6)

2) 下边界 $z=z_{\max }$ 以下为均质岩石，局部不均匀体的异常场在 $z_{\max }$ 上为零，电磁波在 $z_{\max }$ 以下的传播方程为

$E_x=E_x^{*}{\text{e}}^{-kz}$ (7)

其中 $E_x^{*}$ 是常数、 $k=\sqrt{-\mathrm{i}\omega \mu \sigma }$ ， $\sigma$ 是 $z_{\max }$ 以下岩石的电导率。

式(7)对 $E_x$ 求偏导，即得 $z_{\max }$ 处的边界条件为

${\left(\frac{\partial E_x}{\partial z}+k{E}_x\right)|}_{z=z_{\max }}=0$ (8)

3) 取左右边界 $y=y_{\min }$ 、 $y=y_{\max }$ 离局部不均匀体足够远，电磁场在 $y_{\min }$ 、 $y_{\max }$ 上左右对称，其上的边界条件是

${\frac{\partial E_x}{\partial y}|}_{y=y_{\min }}={\frac{\partial E_x}{\partial y}|}_{y=y_{\max }}=0$ (9)

根据电场 $E_x$ 满足的偏微分方程以及相应的定解条件，利用有限差分法可以得到离散化的电场值 $E_x$ 。

3. 倾子响应特点分析

3.1. 简单异常体模型

选取的单个异常体模型如图2所示，均匀半空间(电阻率值为100 Ω×m)存在一个低阻异常体(电阻率值为10 Ω×m)，异常体在水平方向上的位置为3 km至5 km之间、深度方向上的位置为−1 km至−3 km之间。正演模拟过程中，观测点数为33个(点距0.25 km)，采用的记录频点为40个。

单个异常体模型的倾子响应结果(包括实部、虚部和振幅)如图3所示。从图上可以很好的判别出异常体的横向分布情况，说明倾子响应可作为定性分析判别地电模型的横向不均匀性。同时，在倾子响应的实部等值线图中，横向不均匀体的位置介于实部最大值和最小值之间的区域。

3.2. 地垒构造模型

构制的第二个模型为地垒构造地电模型，如图4所示。均匀半空间的电阻率值设置为100 Ω×m，地垒构造的电阻率值设置为1 Ω×m。

图5为计算所得的地垒构造模型倾子响应拟断面图(包括倾子响应的实部、虚部和振幅)，从倾子响应

Figure 1. Boundary conditions of 2D geo-electric model

图1. 二维地电模型的边界示意图

Figure 2. Simple model with a low resistivity anomaly

图2. 简单电阻率异常体模型

Figure 3. MT tripper responses for the simple model with finite difference method

图3. 单个异常体模型的MT倾子响应差分模拟结果

Figure 4. 2D host structure model

图4. 二维地垒构造模型

拟断面图上可以定性判别出地垒构造的横向非均匀性。

4. 倾子响应的影响分析

4.1. 低阻覆盖层影响

选取的地电模型如图6所示，均匀半空间(电阻率值为100 Ω×m)存在低阻异常体(电阻率值为10 Ω×m)，

Figure 5. MT tripper responses for the host structure model with finite difference method

图5. 地垒构造模型的MT倾子响应差分模拟结果

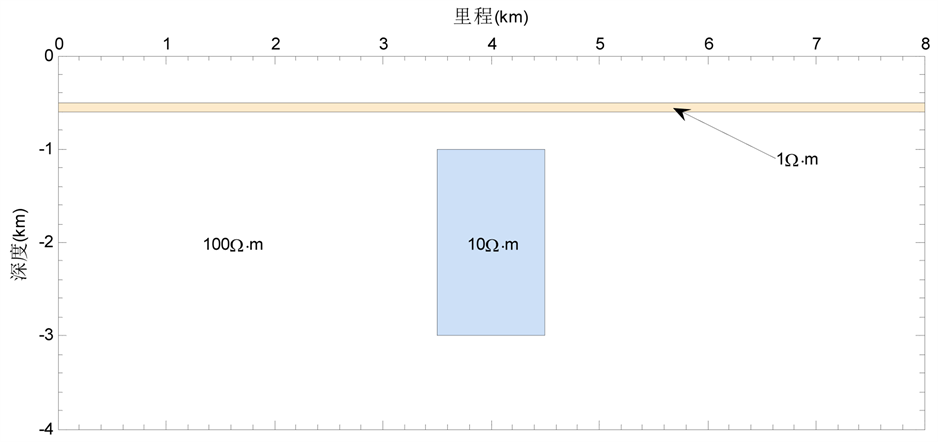
Figure 6. Sketch of a low-resistivity cover model

图6. 低阻覆盖层模型示意图

在深度−500 m处存在一低阻覆盖层，其电阻率值为1 Ω×m、厚度为100 m。

数值模拟过程中，分别对存在低阻覆盖层模型与不存在低阻覆盖层模型进行了正演计算。当不存在低阻覆盖层时，视电阻率拟断面图(见图7(a))很好的反映出低阻异常体的分布情况，倾子响应拟断面图(见图7(c)、(e)、(g))能反映出不均匀体的横向分布情况；当存在低阻覆盖层时，视电阻率拟断面图(见图7(b))已经很难反映出低阻异常体的分布情况，但倾子响应拟断面图(见图7(d)、(f)、(h))仍然可以反映出异常体的横向不均匀分布情况。所以可知，低阻覆盖层对于定性分析大地电磁的倾子响应资料是不存在影响的，而对于定性分析视电阻率资料的影响较大。

4.2. 静位移模型的倾子响应分析

选取的静位移模型如图8所示，均匀半空间(电阻率值为100 Ω×m)存在低阻异常体(电阻率值为10 Ω×m)，而近地表处存在一个电阻率值为1 Ω×m的低阻不均匀体，低阻不均匀体厚10 m、宽1000 m。

图9为模拟所得的倾子响应拟断面图，倾子响应的实部、虚部和振幅均能反映出不均匀体的横向分布情况，并且还能分辨出地表不均匀体的横向不均匀性。因此，静态位移模型对二维倾子响应是没有影响的，这也与TE极化模式的大地电磁响应不存在静态效应是吻合的。

5. 结语

1) 对典型二维地电模型的倾子响应进行了模拟，倾子响应能较好的判别出异常体的横向分布情况，且横向不均匀体的位置介于倾子实部的最大值与最小值之间，这能为实测数据的定性解释提供指导作用。

2) 低阻覆盖层对于定性分析大地电磁的倾子响应资料是不存在影响的，而对于定性分析视电阻率资料的影响较大。

3) 大地倾子电磁倾子响应的异常值很小，而且容易受到环境噪声的干扰，导致倾子响应的信噪比较低。因此，利用倾子响应作定性解释与定量解释时，一定要慎重。

4) 若将大地电磁倾子响应与二维大地电磁反演技术相结合，必能充分发挥大地电磁的技术优势和特点，进而能完善大地电磁基本理论和应用技术。

(a) (b) (c) (d) (e) (f) (g) (h)

Figure 7. MT tripper responses for the low-resistivity cover model with finite difference method

图7. 低阻覆盖层模型的大地电磁响应数值模拟结果

Figure 8. The static geo-electric model

图8. 静位移地电模型

Figure 9. MT tripper responses for the static model with finite difference method

图9. 静态位移模型的MT倾子响应数值模拟结果

基金项目

国家自然科学基金(41674080)。

NOTES

^*通讯作者。