基于三维建模的创意桌设计与实现

Design and Implementation of Creative Table Based on 3D Modeling

摘要: 本文提出了一套基于三维建模的圆形折叠桌设计方案。折叠桌撑起的时候桌面为圆形，将桌脚及桌面摊平的时候为实心矩形。该设计方案首先在设定矩形长宽及桌高的前提下，通过建立数学模型，分析折叠桌实现的具体方案，包括设计加工参数、桌脚边缘线数学描述，并用MATLAB仿真折叠桌的动态变化过程。然后对任意矩形长宽和桌高的情况建立数学模型，给出满足稳固性好、用材节约条件的最优设计方案。最终达到可折叠桌更加实用、更加美观、更加创新的设计效果。

Abstract: This paper proposes a set of circular folding table design based on three-dimensional modeling. When the folding table is propped up, the table top is round. When the table legs are flattened, the table top is a solid rectangle. Firstly, the length and width of the rectangle and the height of the ta-ble are set. The design scheme analyzes the specific scheme of the folding table by setting up the mathematical model. This process includes the design of the processing parameters and the mathematical description of the edge line of the table leg. Moreover, MATLAB is used to simulate the dynamic change of the folding table. Then, a mathematical model is established as for arbitrary rectangle length, width and table height, and an optimal design scheme is given which can design table with good stability and saving material. Ultimately, a more practical, more beautiful, and more innovative folding table is designed.

1. 引言

随着经济的快速发展，创新变得越发重要，可谓是社会进步不可或缺的一股力量。现今，人们的物质生活变得越来越多元化，也日趋高雅，比如家里桌椅、家具、电器等，不仅需要健全的功能，而且也需要独具创意的设计。

早些年前，市场上就出现了比如折叠沙发、折叠桌椅、折叠床等产品，但大都只是名字上的噱头，并没有充分地体现出实用性、美观性以及创意性。就折叠桌而言，市面上大多数的折叠桌都只有简单的桌脚折叠、桌面对折等，太过单调且没任何创意，本文提出的一套基于三维建模 [1] - [6] 的创意折叠桌设计方案，摆脱了现有折叠桌椅的一贯诟病，达到了更好的实用性和创意效果。

2. 折叠桌总方案

本文设计的折叠桌桌面呈圆形，桌腿随着铰链的活动可以平摊成一张平板，如图1所示。桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条中心位置上，并且沿木条有空槽以保证滑动的自由度如图2所示，桌子外形由直纹曲面构成，造型美观。

3. 限定条件模型

本章讨论假定长方形平板尺寸为120 cm × 50 cm × 3 cm，每根木条宽2.5 cm，折叠后桌子高度为53 cm的条件下具体设计方案。

因为该折叠桌桌腿两边对称，只需要对一组桌腿进行分析。平放时，钢筋处于滑槽左端点，折叠时钢筋沿着滑槽向桌脚方向移动最终到达滑槽右端点，此时二十根木条形成了一个曲面。建立空间直角坐标系得到木条的动态方程和木条形成的曲面方程，从而来描述折叠桌的动态变化过程，再根据具体的数据计算出滑槽长度。

3.1. 模型建立

3.1.1. 确定滑槽模型

建立以桌面中心为圆心，桌面为XOZ平面，垂直桌面为Y轴的空间直角坐标系，设第一根木棍与钢筋节点到桌面直径距离为 $D_1$ ，a为第一个木棍与桌面交点到桌面的直径的距离，滑槽长为 $L_n$ ，如图3所示。

Figure 1. Folding table image

图1. 桌子折叠效果图

Figure 2. The steel bar and the empty slot position schematic diagram

图2. 钢筋与空槽位置示意图

Figure 3. Model diagram

图3. 模型图

当最外面的木棍绕Z轴旋转 角度得到旋转面：

$S:\{\begin{array}{l}x=\left(D_1-a\right)\cos t+a\\ y=\left(D_1-a\right)\sin t\end{array}$

每根木条上都存在点 $M^{\prime }\left(x^{\prime },0,z\right)\in l_i$ ，其中 $l_i$ 为任一木条开槽，旋转后 $l_i$ 与旋转面交点为 $M_t$ ，即有：

$M_t:\{\begin{array}{l}x-a=\left(D_1-a\right)\cos t\\ y=\left(D_1-a\right)\sin t\\ z=z\end{array}$

$M^{\prime }{M}_t=\left(\left(D_1-a\right)\cos t+a-x^{\prime },\left(D_1-a\right)\sin t,0\right)$

${x^{\prime }}^2+z^2=r^2$ (r为桌面半径)

在第一条木棍与桌面的夹角t随着折叠的幅度变大逐渐变大，当t最小时，桌子平放， $M^{\prime }{M}_t$ 最小时，钢筋处于滑槽最低端， $M^{\prime }{M}_t$ 最大。则滑槽长为：

$L_n=\max \left|M^{\prime }{M}_t\right|-\min \left|M^{\prime }{M}_t\right|\left(1\le n\le 10\right)$

3.1.2. 确定桌脚模型

因为存在 $M\left(x,y,z\right)\in M^{\prime }{M}_t$ ，则由共线向量的性质有：

$M^{\prime }M=k{M}^{\prime }{M}_t$

$M^{\prime }{M}_t=\left(k\left(\left(D_1-a\right)\cos t+a-x^{\prime }\right),k\left(D_1-a\right)\sin t,0\right)$

$M^{\prime }M=\left(x-x^{\prime },y,z\right)$

所以有：

$\{\begin{array}{l}x-x^{\prime }=k\left[\left(D_1-a\right)\cos t+a-x^{\prime }\right]\\ y=k\left(D_1-a\right)\sin t\end{array}$

消去k得到桌脚线扫过的曲面方程：

$\frac{y}{x-x^{\prime }}=\frac{\left(D_1-a\right)\sin t}{\left(D_1-a\right)\cos t+a-x^{\prime }}$

即桌脚线方程为：

$\{\begin{array}{l}x=\sqrt{r^2-z^2}+k\left[\left(D_1-a\right)\cos t-\sqrt{r^2-z^2}\right]\\ y=k\left(D_1-a\right)\sin t\\ z=0\end{array}$

3.2. 模型求解

平放时，钢筋处于木棍中心，即有：

$x^{\prime }=\sqrt{r^2-z^2}=\sqrt{r^2-{\left[\left(10-n\right)d\right]}^2}$

已假定木条宽 $d=2.5\text{cm},r=25\text{cm}$ ，

因为钢筋处于木棍中心，即有：

$a=\sqrt{r^2-{\left(r-d\right)}^2}=7.8\text{cm}$

$D_1=\frac{60-a}{2}+a=33.9\text{cm}$

折叠后，t达到最大，桌底部高 = 桌高 − 桌面厚度，即： $53-3=50\text{cm}$ ，

$\sin t=\frac{50}{60-a}=0.958$

将数据带入滑槽模型可以得到第一根到第十根的滑槽长度，由于桌脚是对称的，即可得到第十一根到第十九根的滑槽长度，具体数据见表1所示。

Table 1. Slideway length table

表1. 滑槽长度表

3.3. MATLAB仿真

根据确定的滑槽模型以及桌角线模型和确定参数，通过MATLAB [7] - [15] 仿真折叠桌折叠过程中的动态效果，如图4所示，截取了动态效果中的部分图片。

4. 不限条件模型

本章在没有设定条件的情况下讨论。通过得到滑槽左右端点坐标来计算滑槽长度和钢筋位置，再利用共线向量得到直纹曲面方程和截线方程。再进行板材的优化，在保证稳固性良好的情况下尽可能的节省材料。

4.1. 模型建立

同样建立图3坐标系。不妨设：

桌腿与桌面交点坐标为 $M^{\prime }\left(x^{\prime },0,z\right)$ ，其中 $x^{\prime }=f\left(z\right)$ ，

平放时钢筋与木腿交点 $M_0\left(D_1,0,z\right)$ ，

滑槽中心线的Z轴坐标为 $z_i$ ，

滑槽的左右端点分别为 $u_i$ ， $v_i$ ，

木条宽度为d

4.1.1. 确定滑槽模型

最长木腿的折叠角度为t，且该木腿与桌面的交点到桌面直径的距离为a。旋转后，钢筋与木腿桌面的交点的距离相对于平放时变大了，而到底变大了多少则是需要考虑的。为了表示出这个距离，首先建立一个辅助旋转面方程，该方程由最长木腿旋转形成，方程组如下：

$S:\{\begin{array}{l}x=\left(D_1-a\right)\cos t+a\\ y=\left(D_1-a\right)\sin t\\ z=z\end{array}$

旋转后与旋转面交点为 $M_t$ ，即有：

$M_t:\{\begin{array}{l}x-a=\left(D_1-a\right)\cos t\\ y=\left(D_1-a\right)\sin t\\ z=z\end{array}$

$M^{\prime }{M}_t=\left(\left(D_1-a\right)\cos t+a-x^{\prime },\left(D_1-a\right)\sin t,0\right)$

由于折叠幅度的不同滑槽的长度也不同，首先需要确定t的变化范围，桌子折叠时第一条木腿与地面相交情况如图5所示。

由图5可看出：

Figure 4. Dynamic effect diagram

图4. 动态效果图

Figure 5. Leg-ground intersection diagram

图5. 木腿与地面相交情况图

$\sin t=\frac{H-3}{\frac{L}{2}-a}$

其中H为桌子高度，L为平板长度，假定厚度 $d=3\text{cm}$ 。

设 $0\le t\le t_0$ ，则：

$t_0=\arcsin \frac{H-3}{\frac{L}{2}-a}$

即：

$0\le t\le \arcsin \frac{H-3}{\frac{L}{2}-a}$

当桌子折叠0度时，钢筋处于滑槽上端点， $M^{\prime }{M}_t$ 最小， $t_0$ 最大时，钢筋到达下端点， $M^{\prime }{M}_t$ 最大。不妨设：

$\partial \left(t\right)=\left|M^{\prime }{M}_t\right|=\sqrt{{\left(D_1-a\right)}^2-2\ast \left(D_1-a\right)\left(x^{\prime }-a\right)\cos t+{\left(x^{\prime }-a\right)}^2}$

对任意一根桌腿来说，其滑槽的左右端点可以通过 $f\left(t\right)$ 的极差来求解。其平放时的示意图如图6所示：

此时滑槽的长度可以由 $v_i-u_i$ 算出，其滑槽端点公式为：

$v_i=\partial \left(t_0\right)=\sqrt{{\left(D_1-a\right)}^2-2\ast \left(D_1-a\right)\left(f\left(z_i\right)-a\right)\cos t_0+{\left(f\left(z_i\right)-a\right)}^2}$

$u_i=\partial \left(0\right)=\sqrt{{\left(D_1-a\right)}^2-2\ast \left(D_1-a\right)\left(f\left(z_i\right)-a\right)+{\left(f\left(z_i\right)-a\right)}^2}$

$L_p=v_i-u_i$

其中 $x^{\prime }=f\left(z\right)=\sqrt{r^2-z^2}$ 。

为了使桌腿两边对称，故每一边有2p个木条对称分布在X轴两边，如图7所示。

在X轴上方的木条的滑槽左右端点边与X轴重合的木条为第一根，依次从下向上第2根…第i根，其中 $1\le i\le p$ ，则：

$z_1=\frac{1}{2}d,z_2=\frac{1}{2}d+d,\cdots ,z_i=\frac{1}{2}a+\left(i-1\right)d$

由上述公式可以计算出第i木条滑槽的左右端点 $v_i,u_i$ 。

Figure 6. Schematic diagram when laying flat

图6. 平放时示意图

Figure 7. Table leg schematic diagram

图7. 桌腿示意图

4.1.2. 确定桌脚模型

当折叠到t角度时直纹曲面方程为 ${{\displaystyle \sum }}^{\text{}}t$ ，存在 $M\left(x,y,z\right)\in {{\displaystyle \sum }}^{\text{}}t$ ，则过M作xoy平面的平行平面α，则α与x0z平面和直线 $l_1$ 分别有交点 $M^{\prime },M_0$ ，过 $M^{\prime }{M}_0$ 的直线与柱面由交点 $M_t$ ，即 $M,M^{\prime },M_t$ 在同一直线上。则：

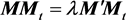
带入各点坐标得：

消去λ，得到曲面方程：

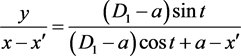
当，得到截痕方程：

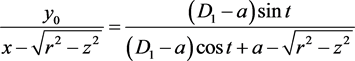
当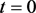时，曲面即为平面；

当时，得到曲面：

在范围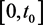中取不同的值，可以得到相应的曲面。

4.2. 目标优化

首先考虑稳定性，旋转后形成由桌面、最外的两条桌腿、中间木条和钢筋所组成的立体图如图8所示。

将上图的桌腿沿着钢筋方向平移与第一根木棍相交形成三角形。其中l为第一个木条的左端点到钢筋的距离，由余弦定理得：

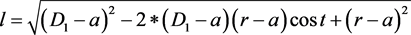
要使三角形稳定，只需，即等腰三角形稳定性好，即：

解得：

其中：，D为平放时桌脚到直径的距离。

在折叠桌稳固的前提下，考虑材料的节省。半边板材面积：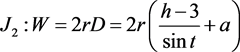

由于节省指标J₂与稳固指标J₁不一致，所以将稳固性排在第一位，在稳固性满足的条件下尽可能的节省材料。

第一步：给定初始角度，代式子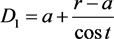，若有解，得到；

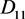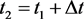第二步：给定一个变化角度，则由，代入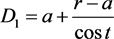，若有解，得到；

…

重复上面步骤，直到无解，此时得到的参数为最优值。其中。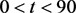

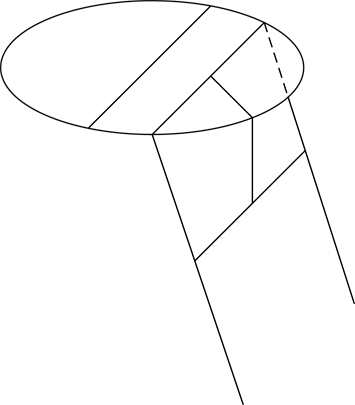
Figure 8. Schematic diagram of stereogram

图8. 立体图示意图

5. 总结

本文给出了一款非常具有创意的折叠桌设计方案。该方案首先在限定材料尺寸和桌高前提下，通过建立数学模型，分析折叠桌实现的具体方案，确定具体模型，并用MATLAB仿真。然后对不限定材料尺寸等条件的情况建立数学模型，给出满足稳固性好、用材节约条件的最优设计方案。本文给出的折叠桌设计方案实用性强、外形美观、独具创新，具有很好的推广价值。

NOTES

^*通讯作者。