1. 简介
Dynkin对策问题一般是如下叙述的。分别定义下价值和上价值函数为
(1.1)
和
(1.2)
其中
是满足一定条件的关于停时
和
的一个函数,那么通常是要寻找充分条件使得
成立.
很容易看出,
,为了得到相反的不等式,我们通常去寻找一对停时
使得
(1.3)
对任意取值于t和T之间的停时
和
成立。
事实上,如果(1.3)成立,那么由$1.1)和(1.2)的定义有
。这时V(t)称为Dynkin对策的价值函数。
研究这类问题的方法有很多。首先,停时对策是最优停时问题的推广,因此可以用鞅方法来寻找一组鞍点并由此得到价值函数。这是比较经典的一种方法,详细研究可以参考E. B. Dynkin [1] ,N. V. Krylov [2] 等。其次,因为带下反射的反射倒向随机微分方程(简称RBSDE) 是解决最优停时的有力工具,有些文章比如J. Cvitanic;I. Karatzas [3] ,S. Hamadene;J. -P. Lepeltier [4] 等,便通过对带上下反射的双边反射BSDE的研究来讨论Dynkin对策问题。再次,特殊地,在马尔科夫情形下,A. Bensoussan,A. Friedman [5] 和A. Friedman [6] 则使用分析的方法来解决微分对策问题。他们通过相应的偏微分方程、变分不等式、自由边界问题的研究来讨论对策问题的鞍点和价值函数。当然,仍然还有其它的方法来解决这个问题,比如I. Karatzas [7] 中的依路径方法和I. Karatzas;H. Wang [8] 中的奇异控制方法。
受J. Cvitanic;I. Karatzas [3] 的启发,在本文中,我们研究存在限制条件情形下的停时对策,既用
期望来计量回报过程。我们分别定义下价值和上价值函数为
(1.4)
(1.5)
其中
为取值于t和 T之间的停时集合,T为终端时刻。在
和
满足适当假设的前提下,我们想去寻找一对鞍点
使得
(1.6)
对任意
成立,因而由(1.4)和(1.5)的定义,相应地价值函数存在。
这个问题看起来和J. Cvitanic;I. Karatzas [3] 中叙述的非常相似,然而它们之间还是由区别的,尽管我们将证明它们的结果看起来也很相似。为了说明我们的问题的意义,我们将在以后指出它们的不同之处,并研究带限制的情形,即我们用
期望来计量回报过程。
2. 双边反射BSDE及相关结果
给定某个函数
,本文中我们始终需要如下条件
(A1)
对某个M > 0以及任意
成立
(A2)
在适当的概率空间中,我们定义双边反射BSDE,详情可参考J. Cvitanic,I. Karatzas [3] 。
定义1 [带上下反射壁的倒向随机微分方程]
设
为
中的一个随机变量,
满足条件(A1)和(A2)的
可测的函数。考虑
中的满足
a.s
的连续过程。
我们称
循序可测的三元组
,
和
为以
为终端,系数为g,以
(分别从上和从下方反射)为反射壁的BSDE 的解,如果下式成立
i)
ii)
并且
(2.1)
(2.2)
(2.3)
对
几乎处处成立。
过程
是一对随机的与时间有关的反射壁,状态过程X在到达终端
的过程中始终不穿越它们。
J. Cvitanic;I. Karatzas [3] 通过求解停时对策问题,既Dynkin对策问题,来求解这种形式的双边反射BSDE,S. G. Peng and M. Y. Xu [9] 则讨论了反射壁更一般的情形下的双边反射问题。我们仍将在本章中讨论受限的情形下的停时对策问题。
3. 限制情形下的Dynkin对策
在这一节中,我们回顾一些与反射BSDE和Dykin对策问题相关的一些结果。
在J. Cvitanic;I. Karatzas [3] 中,作者证明了如果(X,Y,Z)是反射BSDE的解,那么X(t)和由(1.1),(1.2)定义的Dynkin对策问题的价值函数相等,其中
(I)
更一般地,在S. Hamadene,J. -P. Lepeltier [4] 中,作者讨论了以
(II)
为支付函数的混合零和微分对策问题。
在本文中,当
时,我们可以把
展开为
(III)
其中
是以
为终端的BSDE的解,
。
上述停时对策问题看起来很相似,但有本质的区别。
从上面(I),(II)和(III)的表达式中,我们比较容易看出它们积分项中被积函数的区别。
在(I)中,
是事先确定的;在(II)中,X(s)只依赖于
;但是在我们的问题(III)中,
依赖于停时
利用反射BSDE和BSDE的比较性质或g-鞅理论,我们可以找到非线性g-期望下的Dynkin对策的一组鞍点。
其中的主要原因是g-期望拥有很多和线性期望一样的性质,我们可以从以后的证明中看出,线性在反射BSDE和Dynkin对策的联系中不是关键的。
按照J. Cvitanic;I. Karatzas [3] 的思路,利用g期望理论,我们可以很容易证明下面在非受限情形下的结果。
定理1 假设
并且
。生成元
满足条件(A1),(A2)并且
。假定
是以
为终端的反射倒向随机微分方程(2.1)的解,那么由 (1.4),(1.5)确定的Dynkin对策有一组鞍点
,从而价值函数存在。更进一步,这组鞍点为
(3.1)
和
(3.2)
并且
证明:我们只要证明(1.6)。
先固定
,对任意取值于
的一个停时
,因为
和
,
所以我们有
至此,我们将要证明
(3.3)
对任意取值于
的停时
成立。
由(2.3)和(3.1),(3.2),我们有当
时, ;当
时,
。
;当
时,
。
因此在集合
上,由方程(2.1),我们有
这意味着
(3.4)
在另一方面,当
,类似地,我们有
由此意味着
(3.5)
在(3.4)和(3.5)中取条件g-期望,由g-解的相容性,参考Shige Peng [10] ,我们得到(3.3)。
现在,我们确定
,对任意取值于
的停时
,我们将证明
(3.6)
类似地,当
时,我们有
因此
(3.7)
成立。
当
时,(2.1)成为
而这就意味着
(3.8)
在(3.7)和(3.8)中取g-期望,我们有(3.6)证完。
注记1:比较J. Cvitanic;I. Karatzas [3] 中证明4.1的方法和我们证明定理3.1的方法,尽管它们非常类似,但是我们的好处在于直接利用了g-鞅理论,这样方便我们以后处理带限制的情形。
下面我们讨论带限制的情形,也就是我们用带限制的g-期望,既S. G. Peng;M. Y. Xu [9] 中定义的
期望来计量回报过程。
与没有限制的情形相似,我们分别定义下价值和上价值过程如下
(3.9)
和
(3.10)
其中
。
对任意整数m,令
,我们用
,表示分别以U和L为上下反射壁的
反射BSDE的解。因为
能由惩罚方法得到,由比较定理,
是一列递增过程。
利用这一列过程,我们得到如下的一列停时
(3.11)
和
(3.12)
容易看出
递增并且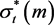 递减。
递减。
令
。为了后面的证明,我们希望
是右连续的,为此我们证明
的右连续性。我们有下面引理
引理1 在函数
,障碍 满足和定理1一样的条件下,
以及其极限
均为右连续。
满足和定理1一样的条件下,
以及其极限
均为右连续。
证明:事实上,令
,
是以U和L为上下反射壁的反射BSDE的解,那么由惩罚方法,
是下列
当
的极限,其中
和
分别是
和
那么由S. G. Peng,M. Y. Xu [9] 中的定理A.1或定理3.1,
右连续从而
右连续。
在以上结果的基础上,我们得到下面带限制的Dynkin对策的结果。
定理2若g和
满足假设(A1)和(A2),
和
是非负连续过程,并且存在
,使得对
,
。我们考虑由(3.9)和(3.10)定义的下价值和上价值函数的Dynkin对策。如果
关于时间递增,那么由(3.13)定义的一对停时是一组鞍点。
证明:如引理1所证明,
是右连续的,我们可以定义停时
(3.13)
并且对任意m,
,
对任意
,由BSDE的比较定理和在非受限的情形下的定理3.1,我们有
(3.14)
对任意
和由(3.11)与(3.12)定义的停时
成立。
在另一方面,我们有
(3.15)
对任意取值于
的停时
成立。
在(3.15)中,我们将要证明
(3.16)
由
和
的定义,我们有
和
因此由
关于时间的单调性,我们得
i) 当
时
ii) 当
时
iii) 当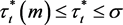 时
时
首先我们在(3.14)和(3.15)中取
时的极限,由(3.16)和
-解的比较定理,我们有
(3.17)
和
(3.18)
然后,我们在(3.17)中取
时的极限。由惩罚方法,
-期望由一列单增的
-期望取极限而得,我们有
(3.19)
把(3.18)和(3.19)放在一起,注意到
和
那么由
-期望的比较性质,我们知道Dynkin对策(3.9)和(3.10)有价值函数
。
更进一步,我们容易看出
是一组鞍点,既如果我们分别在(3.18)和(3.19)令
,则有
(3.20)
证完。
注记 2注意到当
和
时,那么
-解在
上有定义。
事实上,对任意
,假设
对某个实数
成立,那么
是满足限制条件
和终端条件
的g-上解,其中
以及
因此最小g-上解存在。
基金项目
重庆市教育委员会科研基金KJ1400922。