1. 研究背景
区间估计是统计推断的基本任务之一,很多常用的区间估计方法都是基于正态近似。令
是两个独立的二项分布变量,分别服从二项分布
。两个二项分布的比例差定义为
,
的最大似然估计是
,其中
分别是
的最大似然估计。给定
和
,
的方差是
,用
分别替换
得到著名的Wald区间
,
其中
是标准正态分布的
分位数。Fleiss [1] 对Wald区间做了一个连续校正,得到
Mee [2] 使用
的限制最大似然估计
代替最大似然估计
,得到
Beal [3] 引入了一个讨厌参数
,对
重参数化得到
,给定
和
,可以得到
的方差是
,其中
。取
的一个估计
,求解
得到Beal区间
其中
Beal [3] 使用贝叶斯方法得到
,其中
。Beal研究了不同
值得到的区间的小样本行为后建议使用
或
,这两个值对应的Beal区间分别又称为Haldane区间和Jeffreys-Perks区间。Roths & Tebbs [4] 发现,细心选择
值可以提升Beal区间的表现,他们给出了
值的最大似然估计和矩估计,使用这两个
值的区间分别记为
和
。
本文我们关注Beal区间中
值的非对称性问题,提出一种提升Beal区间。
2. 提升Beal区间
Newcomb [5] 通过大量的模拟计算发现,Haldane区间的覆盖率在实际中可以接近0,而Jeffreys-Perks区间虽然可以在一定程度上改善这种情况,但仍然不能彻底避免覆盖率过小的现象。基于此,我们需要改进Beal区间的表现。
记
(2.1)
其中
,则
。对Haldane区间,
,对Jeffreys-Perks区间,
。Beal [3] 取
为
的算术平均,但是
对
的影响可能是不同的,因此,我们取
作为讨厌参数,重参数化得到
,则
假设
是
的一个估计,求解
(2.2)
即得到以两个根为端点的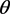 的一个置信区间。经过繁琐的计算可以得到提升的Beal区间
的一个置信区间。经过繁琐的计算可以得到提升的Beal区间

其中
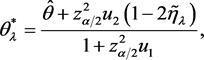

 (2.3)
(2.3)
使用Beal [3] 的贝叶斯方法可以得到
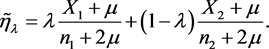 (2.4)
(2.4)
 的值影响区间的端点和中点,我们期望
的值影响区间的端点和中点,我们期望 的均方误差(MSE)达到最小。容易计算得到
的均方误差(MSE)达到最小。容易计算得到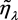 的偏差和方差分别为
的偏差和方差分别为
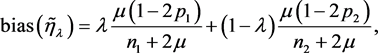

其中 的定义见(2.1)式。最小化
的定义见(2.1)式。最小化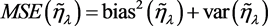 可以得到最优的
可以得到最优的 :
:

其中 。实际中,使用
。实际中,使用 替换
替换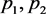 可以得到可用的最优调节参数
可以得到可用的最优调节参数 。
。
3. 模拟
我们使用两个模拟试验验证提升Beal区间的效果,第一个用于检验覆盖率和最小覆盖率,第二个用于检验区间长度。作为对比,我们同时给出Wald方法、Mee方法和Beal方法(包含Roths & Tebbs [4] 改良的两种方法)的模拟结果。
3.1. 检验覆盖率
给定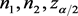 条件下,方法
条件下,方法 的覆盖率定义为
的覆盖率定义为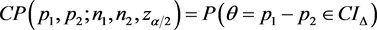 ,最小覆盖率定义为
,最小覆盖率定义为 。取定
。取定 ,分别取
,分别取 和
和 ,计算9种方法的覆盖率和最小覆盖率,结果见图1~图2和表1。
,计算9种方法的覆盖率和最小覆盖率,结果见图1~图2和表1。
从图1~图2和表1可以看出,Mee方法和提升的Jeffreys-Perks方法具有较高的最小覆盖率。
3.2. 检验置信区间长度
我们来评估9种方法的平均区间长度。给定 ,平均区间长度定义为
,平均区间长度定义为

其中 表示区间长度。取定
表示区间长度。取定 ,
, ,分别取
,分别取 和
和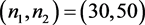 ,取
,取 ,计算9种方法的平均区间长度,结果见表2。我们发现,Wald、Haldane、Beal-MOM、Haldane M和Jeffreys-Perks M方法都具有相对较小的平均区间长度。结合3.1节的覆盖率和最小覆盖的结果,我们推荐使用Jeffreys-Perks M方法,即提升的Jeffreys-Perks方法。
,计算9种方法的平均区间长度,结果见表2。我们发现,Wald、Haldane、Beal-MOM、Haldane M和Jeffreys-Perks M方法都具有相对较小的平均区间长度。结合3.1节的覆盖率和最小覆盖的结果,我们推荐使用Jeffreys-Perks M方法,即提升的Jeffreys-Perks方法。
4. 实例分析
我们使用Wallenstein [6] 的数据,这是一个有关种族歧视的法律案例,详情见原文。这里, 。我们之所以选择这个案例,是因为这里的
。我们之所以选择这个案例,是因为这里的 属于极端情况。判断一种区间估计方法的好坏,其中一个标准就是看这个方法能否恰当地处理这种极端数据。我们使用提升的
属于极端情况。判断一种区间估计方法的好坏,其中一个标准就是看这个方法能否恰当地处理这种极端数据。我们使用提升的
Beal方法估计比例差的95%和99%置信区间。作为对比,我们也给出前述几种方法的估计结果,见表3。我们发现,对于这种极端情况,除了Mee方法和提升的Beal方法,其它方法估计出的区间都超出了[−1,1]的合理范围,这种现象称为overshoot现象,而Mee方法和提升的Beal方法可以避免这种现象的发生。此外,Mee方法和提升的Haldane方法具有相同的估计结果,但是在3.2节的模拟中,Mee方法的平均区

Table 1. Min CP for nine methods
表1. 九种方法的最小覆盖率

Table 2. Mean confidence interval length for nine methods (,)
表2. 九种方法的平均置信区间长度( ,
,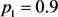 )
)

Table 3. The estimated 95% and 99% confidence intervals for the selected data
表3. 实际数据的95%和99%置信区间
间长度比提升的Haldane方法要大。综上所述,实际中我们推荐使用Mee方法和我们提出的提升Jeffreys-Perks方法。
5. 结论
本文我们通过改良Beal区间中的讨厌参数的选取,提出了一种提升Beal区间方法,最优调节参数可以通过一个显式表达式给出,计算简单。实验模拟显示我们的方法具有大的覆盖率和最小覆盖率,平均区间长度也比较短。实际中,我们推荐使用Mee方法和我们提出的提升Jeffreys-Perks方法。
基金项目
本文为“广东海洋大学人文社会科学项目:二项抽样下两独立总体的比例差的统计推断”项目成果。