链路Pn(m)优美性和序列性

The Gracefulness and Sequences of Pn(m)

摘要: 图G的标号是指G的顶点集到一个整数集的映射g，且对e=uv∈E(G)由g(u)和g(v)诱导出边e的标号。本文给出了链路Pn(m)的k-优美性和序列性。即证明了图Pn(m)是k-优美图和序列图，从而也是调和图。进而推广了原有的一些结果。

Abstract: The labelling of a graph G is injection g of the labels of vertices to a set of integers, and the labels of each edge e= uv are induced by the g(u) and g(v). In the paper, the k-gracefulness and sequence of graphs are given, and we also prove Pn(m) graph is k-graceful, sequential, and harmonious.

1. 引言及主要结果

图的标号理论在编码﹑雷达﹑通信网络﹑射电天文学等方面均有广泛的应用。本文主要研究由路P_n构造的图P_n(m)的k-优美标号和序列标号。文中 $G=\left(V,E\right)$ 表示一个顶点集为V，边集为E且没有孤立点的简单图。文中未提及的术语见 [1]。

定义1：称图 $G=\left(A,B\right)$ 是k-优美(k-graceful)图，如果对任何正整数k，

$f:V\left(G\right)\to \left\{0,1,2,\cdots ,\left|E\right|+k-1\right\}$

使的由

$f^{\prime }\left(uv\right)=\left|f\left(u\right)-f\left(v\right)\right|$

所导出的函数对所有的边 $e=uv\in E\left(G\right)$，其映射

$E\left(G\right)\to \left\{k,k+1,\cdots ,k+\left|E\right|-1\right\}$

是一个双射。称f为G的一个k-优美标号。显然k-优美图，当k = 1时，就是通常所说的优美图。

定义2：称图 $G=\left(A,B\right)$ 是序列图(sequential graph)，如果存在一个单射，

$\theta :V\left(G\right)\to \left\{0,1,2,\cdots ,\left|E\right|-1\right\}$

(如果G是树，则也包含|E|)使的由

${\theta }^{\prime }\left(uv\right)=\theta \left(u\right)+\theta (v)$

所导出的函数对所有的边 $e=uv\in E\left(G\right)$，其映射

$E\left(G\right)\to \left\{c,c+1,\cdots ,c+\left|E\right|-1\right\}$

是一个双射(其中c为某一非负整数)。称 $\theta$ 为G的一个序列标号。

在定义2中的单射 $\theta$，若使函数 ${\theta }^{″}\left(uv\right)=\theta \left(u\right)+\theta \left(v\right)\left(\mathrm{mod}\left|E\right|\right)$ (对 $uv\in E\left(G\right)$ 为边集 $E\left(G\right)\to \left\{0,1,2,\cdots ,\left|E\right|-1\right\}$ 的双射，则称 $$ 为G的一个调和标号。称G为调和图。

由定义2可以看出，若把图的序列标号对边数|E|取摸，就得到了该图的调和标号，即序列标号只是调和标号的特殊情。

定义3：对于自然数 $n\ge \text{3}$，设 $P_n=x_1{x}_2\cdots x_n$ 为n个点的路，在P_n上x_i与x_i+2之间增加 $m_i\ge \text{1}$ 条长为二的路 $x_i{y}_{i,j}{x}_{i+}{}_2$， $i=\text{1},\text{2},\cdots ,n-\text{2}$， $j=\text{1},\text{2},\cdots ,m_i$，所得的图称为链路。记作 $P_n\left(m_1,m_2,\cdots ,m_{n-}{}_2\right)$ 。链路满足

$V\left(P_n\left(m_1,m_2,\cdots ,m_{n-}{}_2\right)\right)=V\left(P_n\right)\cup \left\{y_{i,j}|1\le i\le n-2,1\le j\le m_i\right\}$,

$E\left(P_n\left(m_1,m_2,\cdots ,m_{n-}{}_2\right)\right)=E\left(P_n\right)\cup \left\{x_i{y}_{i,j},y_{i,j}{x}_{i+}{}_2|1\le i\le n-2,1\le j\le m_i\right\}$ .

若 $m_i=m\ge \text{1}$， $\text{1}\le i\le n-\text{2}$，记 $P_n\left(m_{\text{1}},m_{\text{2}},\cdots ,m_{n-}{}_{\text{2}}\right)$ 为P_n(m)。如图1，图2所示。

Figure 1. P₇(2)

图1. 图P₇(2)

Figure 2. P₆(1)

图2. 图P₆(1)

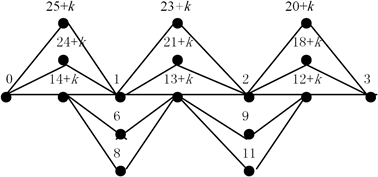
Figure 3. P₇(2) and k-graceful labelling

图3. 图P₇(2)及其k-优美标号

Figure 4. P₆(2) and sequential labelling

图4. 图P₆(2)及其序列标号

本文给出了图P_n(m)的k-优美标号和序列标号。得到了如下定理。

定理1：对于自然数 $n\ge \text{3}$， $m\ge \text{1}$，P_n(m)是k-优美图。

定理2：对于自然数 $n\ge \text{4}$， $m\ge \text{1}$，P_n(m)是序列图。

推论1：( [2] 中定理1)对于自然数 $n\ge \text{3}$，P_n(2)是优美图。

推论2：对于自然数 $n\ge \text{4}$， $m\ge \text{1}$，P_n(m)是调和图。

文中图3是图P₇(2)的k-优美标号，图4是图P₆(2)的序列标号

可以进一步讨论图 $P_n\left(m_{\text{1}},m_{\text{2}},\cdots ,m_{n-}{}_{\text{2}}\right)$ 优美性和序列性，我们有：

问提1：对于自然数 $n\ge \text{3}$， $m_i\ge \text{1}$， $\text{1}\le i\le n-\text{2}$， $P_n\left(m_{\text{1}},m_{\text{2}},\cdots ,m_{n-}{}_{\text{2}}\right)$ 是否是k-优美图？

问提2：对于自然数 $n\ge \text{4}$， $m_i\ge \text{1}$， $\text{1}\le i\le n-\text{2}$， $P_n\left(m_{\text{1}},m_{\text{2}},\cdots ,m_{n-}{}_{\text{2}}\right)$ 是否是序列图？

2. 定理的证明

$\left|V\left(P_n\left(m\right)\right)\right|=mn-2m+n$， $\left|E\left(P_n\left(m\right)\right)\right|=2mn-4m+n-1$ 。

2.1. 定理1的证明

分两重情况定义P_n(m)的顶点标号f如下：

情况1：n为奇数

$f\left(x_{2i-1}\right)=i-1$, $i=\text{1},\cdots ,\left(n+\text{1}\right)/2$,

$f\left(x_{2i}\right)=mn-3m+n-i+k-1$, $i=\text{1},\cdots ,\left(n-\text{1}\right)/2$,

$f\left(y_{2i-1,j}\right)=2mn-2m+n-\left(2m-1\right)i-2j+k-1$, $i=\text{1},\cdots ,\left(n-\text{1}\right)/2$, $j=1,\cdots ,m$,

$f\left(y_{2i,j}\right)=n-2m-2+\left(2m-1\right)i+2j$, $i=\text{1},\cdots ,\left(n-3\right)/2$, $j=1,\cdots ,m$ .

下面验证f是P_n(m)的k-优美标号。

1) 不同的顶点其标号不同。

a) 显然有如下结论：

$f\left(x_{2i-1}\right)\ne f\left(x_{2j-1}\right)$ ( $i\ne j$, $1\le i,j\le \left(n+1\right)/2$ ),

$f\left(x_{2i}\right)\ne f\left(x_{2j}\right)$ ( $i\ne j$, $1\le i,j\le \left(n-1\right)/2$ ),

( i = j 时, ； s = t 时, i ≠ j , 1 ≤ s , t ≤ m , 1 ≤ i , j ≤ ( n − 1 ) / 2 ),

$f\left(y_{2i,s}\right)\ne f\left(y_{2j,t}\right)$ ( $i=j$ 时, $s\ne t$ ； $s=t$ 时, $i\ne j$, $\text{1}\le s,t\le m$, $1\le i,j\le \left(n-3\right)/2$ ).

b) 设

${\text{A}}_0=\left\{f\left(x_{\text{2}i-\text{1}}\right)|\text{1}\le i\le \left(n+\text{1}\right)/2\right\}$, ${\text{C}}_0=\left\{f\left(y_{2i-1,j}\right)|\text{1}\le i\le \left(n-\text{1}\right)/2,\text{1}\le j\le m\right\}$,

${\text{A}}_{\text{1}}=\left\{f\left(x_{\text{2}i}\right)|\text{1}\le i\le \left(n-\text{1}\right)/2\right\}$, ${\text{C}}_{\text{1}}=\left\{f\left(y_{2i,j}\right)|1\le i\le \left(n-3\right)/2,1\le j\le m\right\}$ .

有

${\text{A}}_0\cap {\text{A}}_{\text{1}}={\text{A}}_0\cap {\text{C}}_0={\text{A}}_0\cap {\text{C}}_{\text{1}}={\text{A}}_{\text{1}}\cap {\text{C}}_0={\text{A}}_{\text{1}}\cap {\text{C}}_{\text{1}}={\text{C}}_0\cap {\text{C}}_{\text{1}}=\varnothing$ .

事实上

$\min {\text{A}}_0=f\left(x_1\right)=0$, $\max {\text{A}}_0=f\left(x_n\right)=\left(n-1\right)/2$,

$\min {\text{A}}_1=f\left(x_{n-}{}_1\right)=mn-3m+\left(n-1\right)/2+k$, $\max {\text{A}}_1=f\left(x_2\right)=mn-3m+n-2+k$,

$\min {\text{C}}_0=f\left(y_{n-2,m}\right)=mn-3m+3\left(n-1\right)/2+k$, $\max {\text{C}}_0=f\left(y_{1,1}\right)=2mn-4m+n-2+k$,

$\min {\text{C}}_1=f\left(y_{1,1}\right)=n-1$, $\max {\text{C}}_1=f\left(y_{n-3,m}\right)=mn-3m+\left(n-1\right)/2$ .

于是有 $\min {\text{A}}_0<\max {\text{A}}_0<\min {\text{C}}_1<\max {\text{C}}_1<\min {\text{A}}_1<\max {\text{A}}_1<\min {\text{C}}_0<\max {\text{C}}_0$ 。

2) $\max \left\{f\left(v\right)|v\in V\left(P_n\left(m\right)\right)\right\}=\max {\text{C}}_0=2mn-4m+n-2+k=k+\left|E\left(P_n\left(m\right)\right)\right|-1$ 。

3) 不同的边其标号不同。

$\begin{array}{c}{\text{I}}_1=\left\{\left|f\left(y_{2i-1,j}\right)-f\left(x_{2i-1}\right)\right|,\left|f\left(y_{2i-1,j}\right)-f\left(x_{2i+1}\right)\right||1\le i\le \left(n-1\right)/2,1\le j\le m\right\}\\ =\left\{2mn-4m+n-2+k,2mn-4m+n-3+k,\cdots ,mn-3m+n-1+k\right\}\end{array}$,

$\begin{array}{c}{\text{I}}_2=\left\{\left|f\left(x_{2i}\right)-f\left(x_{2i-1}\right)\right|,\left|f\left(x_{2i}\right)-f\left(x_{2i+1}\right)\right||1\le i\le \left(n-1\right)/2\right\}\\ =\left\{mn-3m+n-2+k,mn-3m+n-3+k,\cdots ,mn-3m+k\right\}\end{array}$,

$\begin{array}{c}{\text{I}}_3=\left\{\left|f\left(y_{2i,j}\right)-f\left(x_{2i}\right)\right|,\left|f\left(y_{2i,j}\right)-f\left(x_{2i+2}\right)\right||1\le i\le \left(n-3\right)/2,1\le j\le m\right\}\\ =\left\{mn-3m-1+k,mn-3m-2+k,\cdots ,k\right\}\end{array}$ .

由(3)显然有 $\forall a,b\in {\text{I}}_i$， $i=\text{1},\text{2},\text{3}$，有 $a\ne b$ 。又因

$\max {\text{I}}_1=2mn-4m+n-2+k$, $\min {\text{I}}_1=mn-3m+n-1+k$,

$\max {\text{I}}_2=mn-3m+n-2+k$, $\min {\text{I}}_2=mn-3m+k$,

$\max {\text{I}}_3=mn-3m-1+k$, $\min {\text{I}}_3=k$ .

得 $\min {\text{I}}_3<\max {\text{I}}_3<\min {\text{I}}_2<\max {\text{I}}_2<\min {\text{I}}_1<\max {\text{I}}_1$，进而有， ${\text{I}}_i\cap {\text{I}}_j=\varnothing$， $i\ne j$， $\text{1}\le i,j\le \text{3}$ 。于是，有 $a\ne b$ 。

4) $\max \left\{f^{\prime }\left(e\right)|e\in E\left(P_n\left(m\right)\right)\right\}=\max {\text{I}}_1=2mn-4m+n-2+k=k+\left|E\left(P_n\left(m\right)\right)\right|-1$ 。

综合(1)~(4)，由优美图的定义知，f是P_n(m)的k—优美标号。故得P_n(m)是k-优美图。

情况2：n为偶数

$f\left(x_{2i-1}\right)=i-1$, $i=\text{1},\cdots ,n/2$,

$f\left(x_{2i}\right)=mn-2m+n-i+k-1$, $i=\text{1},\cdots ,n/2$,

$f\left(y_{2i-1,j}\right)=2mn-2m+n-\left(2m-1\right)i-2j+k-1$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$,

$f\left(y_{2i,j}\right)=n-2m-2+\left(2m-1\right)i+2j$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$ .

类似于情况1的证明，易验证在情况2中f是P_n(m)的k-优美标号。

定理1证毕。

2.2. 定理2的证明

分两重情况定义P_n(m)的顶点标号如下：

情况1： $n\equiv 1\left(\mathrm{mod}3\right)$

情况1.1：n为奇数

$\theta \left(x_{2i-1}\right)=\left(n-1\right)/2+i$, $i=\text{1},\cdots ,\left(n+\text{1}\right)/2$,

$\theta \left(x_{2i}\right)=i-1$, $i=\text{1},\cdots ,\left(n-\text{1}\right)/2$,

$\theta \left(y_{2i-1,j}\right)=2mn-4m+3n-4-3i-2j\left(n-2\right)$, $i=\text{1},\cdots ,\left(n-\text{1}\right)/2$, $j=1,\cdots ,m$,

$\theta \left(y_{2i,j}\right)=2mn-4m+5\left(n-1\right)/2-3i-2j\left(n-2\right)$, $i=\text{1},\cdots ,\left(n-\text{3}\right)/2$, $j=1,\cdots ,m$ .

下面验证θ是P_n(m)的序列标号。

1) 不同的顶点其标号不同。

a) 设

$\text{B}=\left\{\theta \left(x_{\text{2}i}\right)|\text{1}\le i\le \left(n-1\right)/2\right\}\cup \left\{\theta \left(x_{\text{2}i-\text{1}}\right)|\text{1}\le i\le \left(n+1\right)/2\right\}$,

${\text{C}}_j=\left\{\theta \left(y_{2i-1,j}\right)|1\le i\le \left(n-1\right)/2\right\}$, $j=1,\cdots ,m$,

${\text{D}}_j=\left\{\theta \left(y_{2i,j}\right)|1\le i\le \left(n-3\right)/2\right\}$, $j=1,\cdots ,m$ .

由θ的定义有

$\min \text{B}=0$, $\max \text{B}=n$,

$\min {\text{C}}_j=2mn-4m+\left(3n-5\right)/2-2j\left(n-2\right)$, $j=1,\cdots ,m$,

$\max {\text{C}}_j=2mn-4m+3n-7-2j\left(n-2\right)$, $j=1,\cdots ,m$,

$\min {\text{D}}_j=2mn-4m+n+2$, $j=1,\cdots ,m$,

$\max {\text{D}}_j=2mn-4m+5\left(n-1\right)/2-3-2j\left(n-2\right)$, $j=1,\cdots ,m$,

得 $\begin{array}{l}\min \text{B}<\max \text{B}<\min {\text{D}}_m<\max {\text{D}}_m<\min {\text{C}}_m<\max {\text{C}}_m<\min {\text{D}}_{m-}{}_1<\max {\text{D}}_{m-}{}_1\\ <\cdots <\min {\text{D}}_1<\max {\text{D}}_1<\min {\text{C}}_1<\max {\text{C}}_1\end{array}$ 。于是有 $\text{B}\cap {\text{C}}_j=\text{B}\cap {\text{D}}_j={\text{C}}_j\cap {\text{D}}_j=\varnothing$， $j=1,\cdots ,m$ 。得 $\forall u,v\in V\left(P_n\left(m\right)\right)$，若 $u\ne v$，有 $\theta \left(u\right)\ne \theta \left(v\right)$ 。

2) $\max \left\{\theta \left(v\right)|v\in V\left(P_n\left(m\right)\right)\right\}=2mn-4m+n-3<2mn-4m+n-1=\left|E\left(P_n\left(m\right)\right)\right|$ 。

3) 不同的边其标号不同。

${\text{J}}_0=\left\{\theta \left(x_i\right)+\theta \left(x_{i+}{}_1\right)|1\le i\le n-1\right\}=\left\{\left(n+1\right)/2,\left(n+1\right)/2+1,\cdots ,\left(n+1\right)/2+n-2\right\}$,

$\begin{array}{l}{\text{J}}_{1,j}=\left\{\theta \left(y_{2i-1,j}\right)+\theta \left(x_{2i+1}\right),\theta \left(y_{2i-1,j}\right)+\theta \left(x_{2i-1}\right)|1\le i\le \left(n-1\right)/2\right\}\\ =\{2mn-4m+\left(7n-11\right)/2-2j\left(n-2\right),2mn-4m+\left(7n-11\right)/2-1-2j\left(n-2\right),\\ \cdots ,2mn-4m+\left(5n-7\right)/2-2j\left(n-2\right)\},j=1,\cdots ,m\end{array}$,

$\begin{array}{c}{\text{J}}_{2,j}=\left\{\theta \left(y_{\text{2}i,j}\right)+\theta \left(x_{\text{2}i+\text{2}}\right),\theta \left(y_{\text{2}i,j}\right)+\theta \left(x_{\text{2}i}\right)|\text{1}\le i\le \left(n-\text{3}\right)/2\right\}\\ =\left\{2mn-4m+\left(5n-9\right)/2-2j\left(n-2\right),\cdots ,2mn-4m+\left(3n-1\right)/2-2j\left(n-2\right)\right\},j=1,\cdots ,m\end{array}$,

有

$\begin{array}{c}{\text{J}}_{\text{1}}={\text{J}}_{\text{2},m}\cup {\text{J}}_{\text{1},m}\\ =\left\{\left(3n-1\right)/2,\left(3n-1\right)/2+1,\cdots ,\left(5n-9\right)/2\right\}\\ \cup \left\{\left(5n-7\right)/2,\left(5n-7\right)/2+1,\cdots ,\left(7n-11\right)/2\right\}\end{array}$,

$\begin{array}{c}{\text{J}}_{\text{2}}={\text{J}}_{\text{2},m-\text{1}}\cup {\text{J}}_{\text{1},m-\text{1}}\\ =\left\{\left(7n-9\right)/2,\left(7n-9\right)/2+1,\cdots ,\left(9n-17\right)/2\right\}\\ \cup \left\{\left(9n-15\right)/2,\left(9n-15\right)/2+1,\cdots ,\left(11n-19\right)/2\right\}\end{array}$,

…

$\begin{array}{c}{\text{J}}_m={\text{J}}_{\text{2},\text{1}}\cup {\text{J}}_{\text{1},\text{1}}\\ =\left\{2mn-4m-\left(n-7\right)/2,2mn-4m-\left(n-7\right)/2+1,\cdots ,2mn-4m+\left(n-1\right)/2\right\}\\ \cup \left\{2mn-4m+\left(n+1\right)/2,2mn-4m+\left(n+1\right)/2+1,\cdots ,2mn-4m+3\left(n-1\right)/2\right\}\end{array}$ 。

于是有 ${\text{J}}_i\cap {\text{J}}_j=\varnothing$， $i\ne j$， $0\le i,j\le m$，故得 $\forall e,f\in E\left(P_n\left(m\right)\right)$，若 $e\ne f$，有 $\theta \left(e\right)\ne \theta \left(f\right)$ 。

4) $\begin{array}{c}\text{J}={\text{J}}_0\cup {\text{J}}_{\text{1}}\cup {\text{J}}_{\text{2}}\cup \cdots \cup {\text{J}}_m\\ =\left\{\left(n+1\right)/2,\left(n+1\right)/2+1,\cdots ,2mn-4m+3\left(n-1\right)/2\right\}\\ =\left\{\left(n+1\right)/2,\left(n+1\right)/2+1,\cdots ,\left(n+1\right)/2+\left|E\left(P_n\left(m\right)\right)\right|\right\}\end{array}$ 。

综合(1)~(4)，由序列图的定义知，θ是P_n(m)的序列标号。故得P_n(m)是序列图。

情况1.2：n为偶数

$\theta \left(x_{2i-1}\right)=n/2+i$, $i=1,\cdots ,n/2$,

$\theta \left(x_{2i}\right)=i-1$, $i=1,\cdots ,n/2$,

$\theta \left(y_{2i-1,j}\right)=2mn-4m+3n-4-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$,

$\theta \left(y_{2i,j}\right)=2mn-4m+\left(5n-2\right)/2-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$ .

类似于情况1.1的证明，易验证在情况1.2中θ是P_n(m)的序列标号。

在情况2中，可与情况1同理验证θ是P_n(m)的序列标号。故只给出下列标号，不加验证。

情况2： $n\equiv 0,2\left(\mathrm{mod}3\right)$

情况2.1：n为奇数

$\theta \left(x_{2i-1}\right)=\left(n-3\right)/2+i$, $i=1,\cdots ,\left(n+1\right)/2$,

$\theta \left(x_{2i}\right)=i-1$, $i=1,\cdots ,\left(n-1\right)/2$,

$\theta \left(y_{2i-1,j}\right)=2mn-4m+3n-4-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-1\right)/2$, $j=1,\cdots ,m$,

$\theta \left(y_{2i,j}\right)=2mn-4m+\left(5n-7\right)/2-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-3\right)/2$, $j=1,\cdots ,m$ .

情况2.2：n为偶数

$\theta \left(x_{2i-1}\right)=\left(n-2\right)/2+i$, $i=1,\cdots ,n/2$,

$\theta \left(x_{2i}\right)=i-1$, $i=1,\cdots ,n/2$,

$\theta \left(y_{2i-1,j}\right)=2mn-4m+3n-4-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$,

$\theta \left(y_{2i,j}\right)=2mn-4m+\left(5n-4\right)/2-3i-2j\left(n-2\right)$, $i=1,\cdots ,\left(n-2\right)/2$, $j=1,\cdots ,m$ .

定理2证毕。