不规则区域上Poisson方程的蒙特卡洛马尔科夫链方法求解

The Method of Monte Carlo Markov Chain for Solving the Poisson Equation on Irregular Domain

摘要: 本文研究了不规则区域上泊松方程的蒙特卡洛马尔科夫链方法数值求解。在不规则区域上，微分方程的数值计算通常是困难的。基于有限差分的思想，本文构造了可吸收马尔科夫链来求解不规则区域上的微分方程。不规则区域的数值实验结果表明了该方法的可行性和有效性。该方法为求解不规则区域上的泊松方程提供了一种新的计算思路，并保持了空间方向上二阶收敛阶。

Abstract: In this paper, the Monte Carlo Markov chain method for solving Poisson equation in irregular do-main is studied. In irregular domain, the numerical calculation of differential equations is usually difficult. Based on the idea of finite difference, an absorbable Markov chain is constructed to solve differential equations in irregular domain. The numerical experiments in irregular domain show that the method is feasible and effective. This method provides a new idea for solving Poisson’s equation in irregular region and keeps the second order convergence order.

1. 引言

众所周知，Poisson方程是一种经典的偏微分方程，广泛地应用于静电学，机械工程和理论物理等领域 [1] [2] [3] [4] [5]。由于方程求解域逐渐复杂化，Poisson方程难以得到解析解。传统上人们采用有限差分方法和有限元方法来得到Poisson方程的数值解，但是这两种各有优缺点。有限差分法是一种早期成熟的经典数值方法，在复杂边界的情况下，该方法并不灵活，而且对网格生成的要求非常严格 [6]。而有限元法是一种常用的数值方法，对不同求解域的微分方程具有较强的适应性，但是该方法的计算过程抽象而且复杂 [7]。近年来，蒙特卡洛马尔科夫链方法也越来越引起人们的关注 [8] [9] [10]。蒙特卡洛马尔科夫链方法在求解微分方程时具有良好的边界适应性，并且易于编程实现，是一种非常具有发展前景的数值方法。鉴于以上分析，本文考虑不规则区域上Poisson方程的蒙特卡洛马尔科夫链方法。

首先通过网格剖分构建不规则区域Poisson方程的有限差分方法，进而建立蒙特卡洛随机模型获得Poisson方程的近似解，根据蒙特卡洛随机模型引入马尔科夫链从而获得Poisson方程的数值解。

2. 蒙特卡洛随机模型

本文考虑迪利克雷条件下的Poisson方程

$\{\begin{array}{l}-\Delta u=f\text{in}\text{Ω}\\ u=g\text{on}\text{Γ}\end{array}$ (1)

这里u 表示的是待求解的实函数，x，y为实自变量，并且 $\Gamma$ 为求解域 $\Omega$ 的边界。由于本文考虑的是不规则区域上的Poisson方程，不失一般性，求解域不妨设为图1所示的情况。

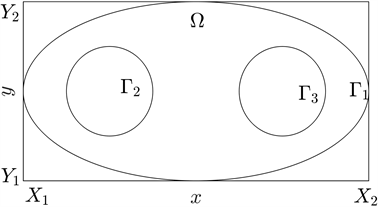
Figure 1. The irregular solution domain of the Poisson equation

图1. Poisson方程的不规则的求解域

图1中， $\Omega$ 表示整个求解域，并且 ${\Gamma }_1,{\Gamma }_2$ 和 ${\Gamma }_3$ 表示求解域的三个边界。下面对整个不规则求解域进行均匀网格剖分来获取网格节点。然而由于不规则边界的存在，网格剖分获得的边界点无法均匀的分布在边界上，如图2所示。

Figure 2. Grid points obtained by mesh generation for irregular domain

图2. 不规则区域剖分获得的网格节点

图2中，蓝色点(见联机版)表示内部网格节点 ${\Omega }_k$ 并且k表示内部网格节点的序列编号。红色点(见联机版)表示由网格剖分获得的边界点 ${\Gamma }_b$ ，这里b表示边界点的序列编号。对于x方向剖分的次数为 $M-1$ ，该方向的剖分步长为 $\Delta x_i\left(i=1,2,\cdots ,M\right)$。并且y方向的剖分次数为 $N-1$ ，其对应的剖分步长为 $\Delta y_j\left(j=1,2,\cdots ,N\right)$。由于生成网格节点的不均匀性，方程(1)不能直接通过二阶中心差分进行离散，下面本文给出了非均匀离散形式的二阶中心差分。

$2\frac{\Delta x_{i-1}\left(U_{i+1,j}-U_{i,j}\right)+\Delta x_i\left(U_{i-1,j}-U_{i,j}\right)}{\Delta x_{i-1}\Delta x_i\left(\Delta x_i+\Delta x_{i-1}\right)}+2\frac{\Delta y_{j-1}\left(U_{i,j+1}-U_{i,j}\right)+\Delta y_j\left(U_{i,j-1}-U_{i,j}\right)}{\Delta y_{j-1}\Delta y_j\left(\Delta y_j+\Delta y_{j-1}\right)}=-f_{i,j}$ (2)

由方程(2)可以得到：

$\begin{array}{l}\frac{1}{\Delta x_i\left(\Delta x_i+\Delta x_{i-1}\right)}{U}_{i+1,j}-\left(\frac{1}{\Delta x_i\left(\Delta x_i+\Delta x_{i-1}\right)}+\frac{1}{\Delta x_{i-1}\left(\Delta x_i+\Delta x_{i-1}\right)}\right)U_{i,j}\\ +\frac{1}{\Delta x_{i-1}\left(\Delta x_i+\Delta x_{i-1}\right)}{U}_{i-1,j}+\frac{1}{\Delta y_j\left(\Delta y_j+\Delta y_{j-1}\right)}{U}_{i,j+1}\\ -\left(\frac{1}{\Delta y_j\left(\Delta y_j+\Delta y_{j-1}\right)}+\frac{1}{\Delta y_{j-1}\left(\Delta y_j+\Delta y_{j-1}\right)}\right)U_{i,j}\\ +\frac{1}{\Delta y_{j-1}\left(\Delta y_j+\Delta y_{j-1}\right)}{U}_{i,j-1}=-\frac{1}{2}{f}_{i,j}\end{array}$ (3)

令 ${\lambda }_1=\frac{1}{\Delta x_i\left(\Delta x_i+\Delta x_{i-1}\right)}$ ， ${\lambda }_2=\frac{1}{\Delta x_{i-1}\left(\Delta x_i+\Delta x_{i-1}\right)}$ ， ${\lambda }_3=\frac{1}{\Delta y_j\left(\Delta y_j+\Delta y_{j-1}\right)}$ ， ${\lambda }_4=\frac{1}{\Delta y_{j-1}\left(\Delta y_j+\Delta y_{j-1}\right)}$ ， $\lambda ={\lambda }_1+{\lambda }_2+{\lambda }_3+{\lambda }_4$ ，可以得到：

$U_{i,j}=\frac{{\lambda }_1}{\lambda }{U}_{i+1,j}+\frac{{\lambda }_2}{\lambda }{U}_{i-1,j}+\frac{{\lambda }_3}{\lambda }{U}_{i,j+1}+\frac{{\lambda }_4}{\lambda }{U}_{i,j-1}+\frac{1}{2\lambda }{f}_{i,j}$ (4)

由方程(4)可知，求解域中的任意内点 ${\Omega }_k$ 的函数值与其四个相邻点的函数值有关。由此可以对其他内点可以建立相同的近似方程，通过简化，可以得到所有内点与边界点的关系，从而可以得到任意内点 ${\Omega }_k$ 的函数值 $U\left({\Omega }_k\right)$。如果有 $N_p$ 个粒子在 ${\Omega }_k$ 点处释放，则这些粒子以方程(4)中对应的概率在网格上随机游

动。网格节点 ${\Omega }_k$ 上粒子的移动方向可根据方程(4)中以 $\left[\frac{{\lambda }_1^k}{{\lambda }^k},\frac{{\lambda }_2^k}{{\lambda }^k},\frac{{\lambda }_3^k}{{\lambda }^k},\frac{{\lambda }_4^k}{{\lambda }^k}\right]$ 为概率生成的随机数R确定，R在 $\left[1,2,3,4\right]$ 取值。其中0表示向左移动，1表示向右移动，2表示向上移动，3表示向下移动，粒子随机游动直至被边界点吸收，这样便构成了蒙特卡洛随机模型。那么任意内点 ${\Omega }_k$ 的函数值可以近似的表示为：

$U\left({\Omega }_k\right)={\displaystyle \underset{b}{\sum }g\left({\Gamma }_b\right)\frac{P_b}{N_p}}+\frac{1}{N_p}\underset{i=1}{\overset{N_p}{{\displaystyle \sum }}}\underset{m=1}{\overset{n_i-1}{{\displaystyle \sum }}}\frac{1}{2{\lambda }^m}f\left({\Omega }_m\right)$ (5)

这里 $P_b$ 表示被边界点 ${\Gamma }_b$ 吸收的粒子的个数， $n_i$ 表示第i个粒子到达边界所运动的步数，即第i个粒子经过了 $n_i-1$ 个内点在第 $n_i$ 次运动后被边界点吸收。 ${\lambda }^m$ 表示在内点 ${\Omega }_m$ 处对应的 $\lambda$ 的值。

3. Poisson方程的蒙特卡洛马尔科夫链方法

为了详细介绍马尔科夫链，下面将对求解域中的内点和边界点进行编号，如图3所示。

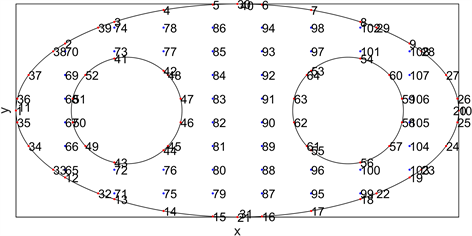
Figure 3. Serial numbers of interior points and boundary points in irregular domain

图3. 不规则区域中的内点和边界点的编号

图3中，内点的个数为 $N_f$ ，边界点的个数为 $N_b$。所有的内点和边界点按照图3的顺序排列成一列，然后每个粒子按照相应的概率移动直到被吸收，显然这是一个可吸收的马尔可夫链，其中马尔可夫链具有 $N_b$ 个可吸收态和 $N_f$ 个不可吸收态。在方程(4)中，在 $U_{i,j}$ 处释放的粒子到 $\left[U_{i+1,j},U_{i-1,j},U_{i,j+1},U_{i,j-1}\right]$ 的概率为它们各自的系数。假设 $\left[U_{i+1,j},U_{i-1,j},U_{i,j+1},U_{i,j-1}\right]$ 的编号为 $\left[m,n,p,q\right]$。对于编号为k的内点 $U_{i,j}$ 概率分布可以表示成下面的形式：

$P_k={\left[0,\cdots ,\frac{{\lambda }_1^k}{{\lambda }^k},0,\cdots ,\frac{{\lambda }_2^k}{{\lambda }^k},0,\cdots \frac{{\lambda }_3^k}{{\lambda }^k},0,\cdots \frac{{\lambda }_4^k}{{\lambda }^k},0,\cdots ,0\right]}_{1\times \left(N_f+N_b\right)}$ (6)

这里 $\left[\frac{{\lambda }_1^k}{{\lambda }^k},\frac{{\lambda }_2^k}{{\lambda }^k},\frac{{\lambda }_3^k}{{\lambda }^k},\frac{{\lambda }_4^k}{{\lambda }^k}\right]$ 分别处在 $P_k$ 的 $\left[m,n,p,q\right]$ 的位置。由于每个网格点都可以确定其概率分布，那么整个马尔可夫链的概率传递矩阵可以得到，记为：

$\mathcal{P}={\left[\begin{array}{cc}I& 0\\ R& Q\end{array}\right]}_{\left(N_f+N_b\right)\times \left(N_f+N_b\right)}$ (7)

其中， ${\mathcal{P}}_{i,j}$ 表示粒子从状态i到状态j的概率，矩阵 $R\left(N_f\times N_b\right)$ 表示粒子从不可吸收状态到可吸收状态的概率，矩阵 $Q\left(N_f\times N_f\right)$ 表示粒子从不可吸收状态到不可吸收状态的概率，矩阵 $I\left(N_b\times N_b\right)$ 表示粒子从可吸收状态到可吸收状态的概率，并且它是一个单位矩阵。矩阵0的元素都是0，表示粒子从可吸收状态到不可吸收状态的概率。对于可吸收马尔可夫链，矩阵 $E-Q$ 具有可逆矩阵，其中E是与Q同阶的单位矩阵。

$N={\left(E-Q\right)}^{-1}$

$N_{i,j}$ 具有一定的实际意义，表示从状态i到状态j的传输路径数。那么对应的可吸收概率矩阵为：

$B=N\cdot R$

那么对于所有内点的函数值可以表示为下面的形式：

$U_{\Omega }=B\cdot g_{\Gamma }+N\cdot {\mathcal{F}}_{\Omega }$ (8)

这里 $U_{\Omega }$ 表示所有内点的函数值， $g_{\Gamma }$ 表示所有边界点的函数值， ${\mathcal{F}}_{\Omega }=\frac{1}{2{\lambda }_{\Omega }}{f}_{\Omega }$ ，并且 $f_{\Omega }$ 表示所有内点对应的f的函数值， ${\lambda }_{\Omega }$ 为相应的内点所对应的 $\lambda$ 的值。这里值得注意的是 $U_{\Omega }$ 所对应的内点的函数值的编号与内点的编号是一致的。

4. 数值实验

为了进一步证明本文提出方法的有效性，本文将使用下面的形式来计算数值收敛阶。

$E^N\left(h\right)={\left|U\left(x_c,y_j\right)-u\left(x_c,y_j\right)\right|}_{\infty },rat{e}_h={\log }_2\left(\frac{E^N\left(h\right)}{E^N\left(2h\right)}\right)$

这里h表示的是在x和y方向上的剖分次数 $M=N$ 时， $h=\Delta x=\Delta y$。 $E^N\left(h\right)$ 表示数值解和精确解之间的最大范数误差， $rat{e}_h$ 表示空间收敛阶，并且 $c=round\left(M/2\right)$。

考虑二维不规则区域上Poisson方程的迪利克雷问题，可以描述为下面的形式：

$\{\begin{array}{l}\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=2{\text{e}}^{x+y},\left(x,y\right)\in \text{Ω}\\ u={\text{e}}^{x+y},\left(x,y\right)\in \text{Γ}\end{array}$

其中 $\Omega \cup \Gamma =\left\{\left(x,y\right)|\frac{x^2}{4}+y^2\le 1,{\left(x-1\right)}^2+y^2\ge \frac{1}{4},{\left(x+1\right)}^2+y^2\ge \frac{1}{4}\right\}$ ，该问题的解析解为 $u={\text{e}}^{x+y}$。

Figure 4. The comparison between the exact solution (right panel) and the numerical solution (left panel) with $M=N=80$

图4. 在 $M=N=80$ 下的解析解(右边)和数值解(左边)的对比

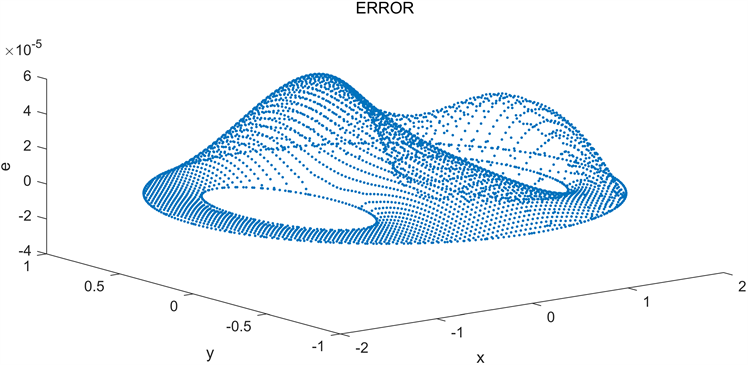
Figure 5. The error obtained by Monte Carlo Markov chain method with $M=N=80$

图5. 在 $M=N=80$ 下的数值解与解析解的误差

Table 1. The numerical convergence order by Monte Carlo Markov chain method

表1. 蒙特卡洛马尔科夫链方法数值收敛阶情况

图4展示了在 $M=N=80$ 下不规则区域上Poisson方程得到的精确解和数值解的比较。可以看出，两者的结果是一致的。图5展示了不规则区域上Poisson方程的数值解与解析解之间的误差，可以清楚的看出两者之间的误差很小。通过表1可以看出由蒙特卡洛马尔科夫链方法获得的数值收敛阶始终在2阶左右，其效果是显著的。

5. 结论

本文引入一种新的蒙特卡罗马尔可夫链方法求解不规则区域上的Poisson方程。数值结果表明了该方法的有效性和适应性。该方法为求解不规则区域上的微分方程提供了一种新的思路。此外，该方法简单，易于编程，还可推广到其它更复杂的微分方程。

参考文献

NOTES

*通讯作者