1. 引言
近年来,四阶微分方程边值问题广泛出现在医学、物理学、生物学等领域,受到了学者的密切关注。由于四阶边值问题起源于弹性梁状态问题的数学模型,此类问题研究比较活跃,有很多学者对四阶方程两点边值问题运用锥拉伸锥压缩不动点定理,上下解方法,单调迭代方法等进行了很好的研究 [1] - [7] ,但是有关复合型的微分方程组边值问题的研究并不多见。文献 [8] 研究了如下四阶复合型微分方程组边值问题多个正解的存在性:
其中非线性项
,
,且
。
受以上文献的启发,本文将考察如下含有
的一类耦合奇异半正微方程组的两点边值问题,通过讨论
的取值,得出
对其正解的存在性及多解性的影响。方程如下:
(1)
假设方程满足如下条件:
(H1)
,且
连续;
(H2)
,
,对
,
,其中
;
(H3)
,且为常数。
定义
为定义在闭区间
上全体连续函数构成的集合,在
上定义范数
,
,在E中取范数
。为了叙述方便,我们引入下列记号
显然K为E中的正规锥。
2. 预备知识
引理1 [1] :(锥拉伸与锥压缩不动点定理)设
与
是无穷维实Banach空间E中的两个有界开集,并且
,
是全连续算子,如果下列条件之一满足:
1)
。
2)
。
则算子A在
中有不动点。
引理2 [4] :边值问题
的格林函数为:
且具有下列性质:
1、当
时,有
,
。
2、
。
由此问题(1)的解等价于
的解。
记
定义算子:
显见问题(1)的解等价于算子T的不动点。
引理3:若方程满足(H1)-(H3),则算子T是全连续的,且
。
证明:由全连续算子的定义易证算子T全连续,下证
。由引理1性质2得
,
,
,则
,当
时,有
即
,
,所以
。
引理4 [9] :设L:
为线性全连续算子,且
,其中K是
中的锥,如果存在
及常数
,使得
,则L的谱半径
且L有一个相应于第一个特征值
的正特征函数
,即
。
引理5:设(H1)-(H3)成立,则算子T的谱半径
,且T有一个对应于第一个特征值
的正特征函数。
证明:因为T为全连续算子,且
。由条件(H1),(H2)知存在
,使得
因此,存在
,使得对于
,满足
,
。
取
,满足
且
,则
又由(H3):
,以及
可得,存在常数
,使得
。由引理4得算子T的谱半径
,且T有一个对应于第一个特征值
的正特征函数。
设
为线性边值问题
的第一个特征值,
为线性边值问题
的第一个特征值,则
。从而
的谱半径
,
的谱半径
。假设它们相对应的特征函数分别为
。则满足
,否则如果
,则
其中
,从而矛盾,不妨设
.在E上定义泛函:
则对
,
。令
,
则
(2)
并且满足:
即
(3)
3. 主要结果
定理1:若条件(H1)~(H3)成立,且
,则问题(1)至少有一个正解。
证明:以下证明分两步
1) 由
可得
且充分小,使得当
时,对 ,恒有
,恒有 。
。
令 ,假设存在
,假设存在 和
和 满足
满足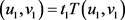 ,则由(3)式得
,则由(3)式得
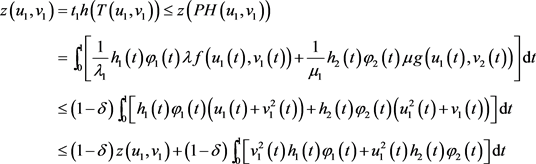
即 ,由(2)式得
,由(2)式得 ,即
,即 ,这与d充分小矛盾。根据不动点指数的同伦不变性得
,这与d充分小矛盾。根据不动点指数的同伦不变性得 。
。
2) 由 可得,
可得, ,使得当
,使得当 时,有
时,有 ,
,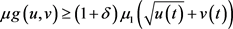 。又当
。又当 时,
时, 有界,故存在常数
有界,故存在常数 ,使得当
,使得当 时,对
时,对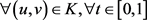 ,恒有
,恒有

取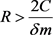 ,令
,令 ,假设存在
,假设存在 和
和 满足
满足 ,其中
,其中 ,则由(3)可得
,则由(3)可得

所以 ,这与
,这与 矛盾,从而假设不成立。故当R充分大时
矛盾,从而假设不成立。故当R充分大时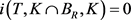 。再由不动点指数的可加性,得
。再由不动点指数的可加性,得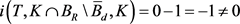 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。
定理2:若条件(H1)~(H3)成立,且 ,则问题(1)至少有一个正解。
,则问题(1)至少有一个正解。
证明:以下证明分两步
1) 由 可得
可得 ,使得当
,使得当 时,对
时,对 ,有
,有
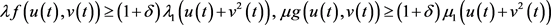
假设存在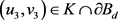 和
和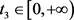 ,满足
,满足 ,其中
,其中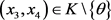 ,则由(3)可得
,则由(3)可得
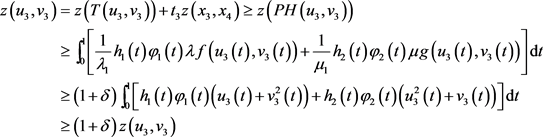
即 ,这与(2)式
,这与(2)式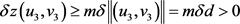 矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有
矛盾,从而假设不成立。由不动点指数的缺方向性知,当d充分小时,有 。
。
2) 又由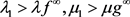 可得,
可得,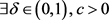 ,使得
,使得 时,有
时,有

取R充分大,满足 ,假设存在
,假设存在 和
和 满足
满足 ,则由(3)式得
,则由(3)式得
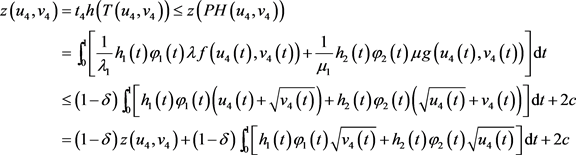
所以
又因为 ,从而
,从而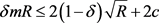 。这与R的选取矛盾,故当R充分大时,有
。这与R的选取矛盾,故当R充分大时,有 。再由不动点指数的可加性得
。再由不动点指数的可加性得 。从而算子T至少有一个不动点,即方程至少有一个解。
。从而算子T至少有一个不动点,即方程至少有一个解。
定理3:若条件(H1)~(H3)成立,对于 ,若存在数
,若存在数 ,使得当
,使得当 时,恒有
时,恒有
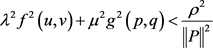
成立,其中 ,那么问题(1)至少有两个正解。
,那么问题(1)至少有两个正解。
证明:令 ,其中
,其中 ,若存在
,若存在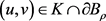 和
和 ,满足
,满足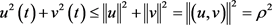 ,由
,由 可得
可得

从而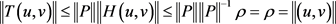 ,故由锥压缩定理知
,故由锥压缩定理知 。
。
利用定理1的第二步和定理2的第一步证明及不动点指数的可加性可得
 ,
,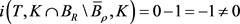
由不动点指数的可解性知,算子T在 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。
定理4:若条件(H1)-(H3)成立,对于 ,若存在数
,若存在数 ,使当
,使当 ,
, 时,恒有
时,恒有

成立,其中 ,则问题(1)至少有两个正解。
,则问题(1)至少有两个正解。
证明:若存在 和
和 ,满足
,满足 ,
,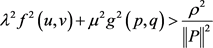 得
得

即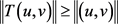 ,故由锥压缩定理知,
,故由锥压缩定理知, 。
。
利用定理1的第一步和定理2的第二步证明及不动点指数的可加性可得
 ,
,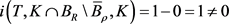
由不动点指数的可解性知,算子T在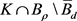 和
和 中分别至少有一个不动点,所以问题(1)至少有两个正解。
中分别至少有一个不动点,所以问题(1)至少有两个正解。
致谢
感谢导师陈芳启教授的悉心指导!
基金项目
国家自然科学基金(11872201)。