1. 引言
随着大型数据集越来越可用和重要,科学技术的最新发展已经引起了数据处理的革命。为了满足“大数据”时代的需要,压缩传感(CS) [1] 领域正在迅速发展。CS的过程包括编码和解码。编码过程涉及一组(线性)测量值
,其中A是一个大小为
的矩阵。如果
,我们称为
能被压缩。译码的过程是从b中恢复x,另外假设x是稀疏的。它可以表示为一个优化问题,
(1.1)
其中
表示
范数。因为
等于非零元素的数目,将
范数最小化,等于求出最稀疏的解。在CS中最大的障碍之一是解决解码问题式(1.1),因为
范数极小化问题的求解在数学上是一个NP [2] 难问题,即在多项式时间内无法有效求解。为了克服上述困难,一种流行的方法是用凸形代替,即
范数极小化
(1.2)
其中
。(1.2)是一个凸优化问题,同时,它可以通过梯度投影法 [3] ,同源性方法 [4] 等来求解。最近,将非凸度量作为
的替代方法的应用不断增加。特别是 [5] [6] 中
的非凸度量p可以看作是近似
随着
的连续策略。优化策略包括迭代重加权 [7] 和半阈值 [6] 。其他非凸
变形包括
[8] ,
(1.3)
结果表明,当测量矩阵A高度相干时,
极小化一致优于经典的
和
极小化,在 [8] 中理论上,给出了一个RIP类型的充分条件,以确保
能精确地恢复稀疏信号。
众所周知,神经网络在优化问题和许多应用中得到了广泛的应用。但是,可能会遇到高相干性的测量矩阵,开发出更好、高效的优化方法是有必要的。本文通过推广
形式,考虑
度量,
(1.4)
显然,这是一个非凸优化问题。应用变量替换以及投影算子 [9] 的知识,我们提出了一种新的无约束
极小化问题的神经网络模型。用这种方法不仅能真正解决问题同时也避免了次梯度项的困难。
2. 问题介绍
通过拉格朗日乘子,我们将问题转换为无约束优化问题
(2.1)
毫无疑问是不可微的,我们首先将目标函数进行转换,而不是直接寻找将非凸目标函数极小化的方法。假设在问题中,用
来代替未知变量x,其中
分别为x中所有的正的和负的元素,也就是说
,
,
,
。有了这样的替换,很容易有
其中
。因此,问题可以改写为
Subject to
(2.2)
这里
是一个正则化参数。这个问题相当于下面的非凸问题
Subject to
(2.3)
其中目标函数
是一个非凸连续微分,并且
3. 神经网络模型
本节介绍了求解CS中
极小化问题的IPNN方法。基于比例梯度投影,建立了求解非凸问题的神经网络模型。令
作为一个最优解,因为
二次可微,则对所有的
和
,有
。因此函数
在
上可微,因为
在
处达到最小值,因此
。则有
(3.1)
找到一个最优值是相当于求解变分不等式,它可以被视为一个在科学和工程领域的一个自然的平衡问题.因此我们的下一个任务是寻求一个适当的方法。由于,我们有以下的惯性投影神经网络IPNN模型
(3.2)
其中
,
是投影算子:
该模型属于一个存在于神经动力学优化模型中的双层结构,克服了一些缺点并且由于内点项
的存在加速了收敛过程。
4. 算法
在这个部分中,优化算法的原则总结在算法1中。该算法基于IPNN模型,提出了重构稀疏信号求解无约束
最小化问题的迭代步骤。由于问题的非凸性,该算法一般不能保证收敛到全局最小,因此一个好的初始化对该算法的性能是至关重要的。一个很好的启发是利用求解无约束的
最小化问题的解来作为这个算法的初始值。我们使用
来将算法初始化,其中
是A的伪逆,则很容易计算
通过
。
5. 数值仿真
在本节进行数值实验来证明我们提出的算法IPNN
的有效性和信号重构能力。所有的实验均在MATLAB上实现,采用的常微分方程求解器是ode15s。从 [8] 中测试了稀疏向量的精确重构在矩阵A较弱的条件下,可以保证问题的最小值的稀疏度。为了验证在A是一个高相干矩阵的情况下的稀疏向量精确重构,我们通过创建一个随机采样部分DCT矩阵
来产生传感矩阵,其中矩阵
。矩阵A的相干性随着正整数F的增加而增加。
的元素在[0,1]上独立同分布。接下来,我们将研究F与相干性之间的关系,其中相干性定义为
。
例1:考虑无约束
极小化问题
(5.1)
首先给出了无噪声情况下问题的稀疏信号重构。测试长度为n的稀疏信号
由标准正态分布生成。由A和
,可由
计算得到b。令
,
,
,
。IPNN
算法的效果可以从图中看出。
图1绘制了产生的矩阵
的相干性结果。很容易看出,
随着F增加趋向于变大,即A的相干性随着F增大而增大。为了方便起见,在不引起混淆的情况下,我们将使用F来表示相干性。因此,在随后的实验中,我们设置F = 14足以保证高相干性测量矩阵。

Figure 2.
contour line plot
图2.
等值线图
图2展示了当
取不同值时的
等值线图。
图3展示了神经网络的解渐近稳定且收敛于局部最优解
。
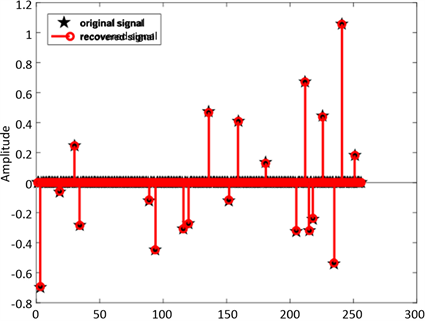
Figure 4. The original signal and reconstructed signal via IPNN
,
图4. IPNN
(
)算法下得原始信号与重构信号
从图4可以直观观察重构结果,显示原始信号和重构信号基本上重合。因此,在无噪声情况下,我们提出的算法IPNN
可以有效重构稀疏信号。
图5展示了50个实验值的平均相对误差,
(
)与
相比,收敛速度更快,且相对误差更小。
例2:在这一部分中,我们考虑了噪声情况下问题(5.1)的鲁棒恢复。我们将白高斯噪声加到干净的数据
中,然后得到测量值
,其中snr对应于以dB测量的信噪比(snr)值。我们
设置初始值
。重构信号
通过算法IPNN
获得,我们计算重构的信噪比通过
。
IPNN是一种通过
[10] 极小化实现稀疏信号恢复的惯性投影神经网络算法。DCA-
[8] 是求解
极小化问题的典型优化方法。通过嵌入
(
)范数噪声约束在最近出现的
方法中,采用了IR
[11] 方法从高相干测量矩阵中恢复一般噪声信号。在下面的实验中,我们设定
。优化算法比如ADMM-lasso [12] 是解决稀疏问题的重要和流行的经典算法。通过噪声的改变,我们在随机过采样部分DCT矩阵和常用随机高斯矩阵上比较了IPNN
(
),IPNN,IR
,DCA-
,ADMM-lasso。对于随机过采样的部分DCT矩阵,我们设
,
。对于高斯矩阵,我们假设
,
。每个记录值是50次随机实现的平均值。

Table 1. Randomly over-sampled partial DCT matrix
表1. 随机过采样部分DCT矩阵
表1显示了使用过采样DCT矩阵得到的结果。相比之下,在中等噪声下,我们的IPNN
表现更佳。
表2显示了高斯测量下的结果。我们的IPNN
也明显优于其他算法。
6. 结论
本文介绍了用IPNN
方法通过
极小化来实现稀疏信号的恢复。为了验证我们方法的有效性和鲁棒性,进行几组对比实验包括噪声和无噪声,以及高斯随机矩阵和高相干矩阵。结果表明,该方法在信号恢复方面优于其它最先进的方法。稀疏信号重构问题其应用广泛而成为一个热点问题,针对稀疏信号重构等相关问题,需要寻找更加实用有效的方法来解决这些非凸问题,结合神经网络,压缩感知将会迎来美好的明天。
基金项目
中央高校基本科研业务费资助项目(No. XDJK2018C076)。