Mie-Grüneisen多介质混合计算模型的Godunov型格式

The Godunov Type Scheme for Multi-Component Mie-Grüneisen Mixture Model

摘要: 本文的主要目的是为了推导Mie-Grüneisen多介质混合模型下的Godunov类型格式。Godunov格式在求解多介质问题的间断面时，通常能得到使数值解保持无振荡。为了适应Mie-Grüneisen多介质混合模型，将二维矩形的Godunov类型格式在有限体积算法下进行了重新构造。数值实验表明，Godunov格式在Mie-Grüneisen混合模型下能很好地相结合。

Abstract: The aim of this article is the deduction of Godunov type scheme for Mie-Grüneisen mixture model. For multi-component problem with discontinuous sections, the Godunov schemes always keep the solution non-oscillation. To adapt to Mie-Grüneisen mixture model, the Godunov fluxes are recon-structed under finite volume method in 2D rectangular grids. According to numerical test, the Go-dunov scheme can couple well with Mie-Grüneisen mixture model.

1. 引言

可压缩流场中的多介质Riemann问题，多年以来一直是研究者们所关注的一个焦点问题 [1] 。流体的运动特性可由欧拉方程描述，而流体的物理性质则由状态方程来描述。相比于其它形式的状态方程，Mie-Grüneisen方式无论是对流体 [2] 还是固体 [3] ，均能很好地描述其力学和热力学特性，因而得到广泛的应用。而薛克明提出的Mie-Grüneisen多介质混合模型 [4] ，则为Mie-Grüneisen方程下的多介质问题提供了很大的便利 [5] 。但是由于Mie-Grüneisen多介质混合模型目前并未得到广泛的重视，这使得它可供参考的数值离散格式仍然比较少 [6] 。而Godunov型格式则是计算流体力学有限体积方法中比较常见的一种格式，因为它能给带有强间断面的问题提供稳定的数值解 [7] 。相比于GFM等数值算法，它省去了其它的数值处理界面的过程 [8] ，仅自身的数值格式便具备较好的分辨率。对于Mie-Grüneisen多介质混合模型来说，其方程系统同时包括Euler守恒方程以及其它热力学参数的非守恒方程，不仅涉及的方程式较为复杂，而且具有很强的非守恒性，Godunov型格式的构造形式将显得非常复杂。

本文在Mie-Grüneisen多介质混合模型下，按照二维有限体积差分方法进行了数值离散化，离散后确定了守恒变量与通量的计算形式，并按特定的时间步长和均匀的空间步长进行数值迭代。该过程中，对Godunov格式下的通量做了细致的推导。为了验证该格式的计算稳定性，利用该模型模拟了一个复杂的二维流场的相互作用问题。

2. 计算方法

2.1. 控制方程组

这里考虑由多种流场介质共存的二维可压缩流场，那么整个流场的运动可以由欧拉方程来描述：

$\{\begin{array}{l}\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}\left(\rho u\right)+\frac{\partial }{\partial y}\left(\rho v\right)=0\\ \frac{\partial \left(\rho u\right)}{\partial t}+\frac{\partial }{\partial x}\left(\rho u^2+p\right)+\frac{\partial }{\partial y}\left(\rho uv\right)=0\\ \frac{\partial \left(\rho v\right)}{\partial t}+\frac{\partial }{\partial x}\left(\rho uv\right)+\frac{\partial }{\partial y}\left(\rho v^2+p\right)=0\\ \frac{\partial \left(\rho E\right)}{\partial t}+\frac{\partial }{\partial x}\left(\rho Eu+pu\right)+\frac{\partial }{\partial y}\left(\rho Ev+pv\right)=0\end{array}$ (1)

式中，r为密度，u、v分别为横向和纵向速度，E为能量，p为压力。欧拉方程(1)需要结合状态方程才能完成求解。这里使用Mie-Grüneisen状态方程：

$p-p_{ref}\left(\rho \right)=\rho \Gamma \left(\rho \right)\left(e-e_{ref}\left(\rho \right)\right)$ (2)

这里，G、p_ref、e_ref分别是由流体物理特性决定的热力学参数 [4] 。由于G、p_ref、e_ref通常都具有复杂的函数表达式，可以考虑利用非守恒型方程来对它们进行分别求解 [5] ：

$\{\begin{array}{l}\frac{\partial }{\partial t}\left(\frac{1}{\Gamma }\right)+u\frac{\partial }{\partial x}\left(\frac{1}{\Gamma }\right)+v\frac{\partial }{\partial y}\left(\frac{1}{\Gamma }\right)+\rho \varphi \frac{\partial u}{\partial x}+\rho \varphi \frac{\partial v}{\partial y}=0\\ \frac{\partial }{\partial t}\left(\frac{p_{ref}}{\Gamma }\right)+u\frac{\partial }{\partial x}\left(\frac{p_{ref}}{\Gamma }\right)+v\frac{\partial }{\partial y}\left(\frac{p_{ref}}{\Gamma }\right)+\rho \phi \frac{\partial u}{\partial x}+\rho \phi \frac{\partial v}{\partial y}=0\\ \frac{\partial }{\partial t}\left(\rho e_{ref}\right)+u\frac{\partial }{\partial x}\left(\rho e_{ref}\right)+v\frac{\partial }{\partial y}\left(\rho e_{ref}\right)+\rho \psi \frac{\partial u}{\partial x}+\rho \psi \frac{\partial v}{\partial y}=0\end{array}$ (3)

其中f、j、y代表1/G、p_ref/G、re_ref对密度r的导数项。

对于多介质流场，需要对界面进行捕捉。假设质量分数为Y_I，界面的运动可以通过以下方式来求解：

$\frac{\partial \left(\rho Y_{\text{I}}\right)}{\partial t}+\frac{\partial \left(\rho Y_{\text{I}}u\right)}{\partial x}+\frac{\partial \left(\rho Y_{\text{I}}v\right)}{\partial y}=0,i=1,2,\cdot \cdot \cdot ,m-1$ (4)

将守恒方程(1)、非守恒方程(3)和界面运动方程(4)联立起来，即可得到整个Mie-Grüneisen多介质混合模型的求解方程组。

2.2. 有限体积算法

Mie-Grüneisen多介质混合模型的有限体积格式可以表示成如下所示的形式：

$\frac{W_j^{n+1}-W_j^n}{\Delta t}+\frac{F_{i+1/2,j}-F_{i-1/2,j}}{\Delta x}+\frac{G_{i,j+1/2}-G_{i,j-1/2}}{\Delta y}=0$ (5)

这里Δt为时间步长，Δx、Δy为空间步长。W代表变量，分别用F、G表示x、y方向的通量。角标i和j分别代表x、y方向的节点序号，n为时间步长的序号。变量和通量各自的表达式分别为：

$W=\left\{\begin{array}{c}\rho \\ \rho u\\ \rho v\\ \rho E\\ 1/\Gamma \\ p_{ref}/\Gamma \\ \rho p_{ref}\\ \rho Y_{\text{I}}\end{array}\right\}$ ， $F=\left\{\begin{array}{c}\rho u\\ \rho u^2+p\\ \rho uv\\ \left(\rho E+p\right)u\\ \rho \varphi u\\ \rho \phi u\\ \rho \psi u\\ \rho Y_{\text{I}}u\end{array}\right\}+u\left\{\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1/\Gamma \\ p_{ref}/\Gamma \\ \rho p_{ref}\\ 0\end{array}\right\}$ ， $G=\left\{\begin{array}{c}\rho u\\ \rho uv\\ \rho v^2+p\\ \left(\rho E+p\right)v\\ \rho \varphi v\\ \rho \phi v\\ \rho \psi v\\ \rho Y_{\text{I}}v\end{array}\right\}+v\left\{\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1/\Gamma \\ p_{ref}/\Gamma \\ \rho p_{ref}\\ 0\end{array}\right\}$

Godunov型的通量F和G，其表达形式如下 [7] ：

$\{\begin{array}{l}{F}_{i+1/2,j}=\frac{1}{2}\left[F_L{}_{i+1/2,j}+F_R{}_{i+1/2,j}-\hat{R}\left|\hat{\Lambda }\right|\hat{L}\left(W_L{}_{i+1/2,j}-W_R{}_{i+1/2,j}\right)\right]\\ G_{i,j+1/2}=\frac{1}{2}\left[G_L{}_{i,j+1/2}+G_R{}_{i,j+1/2}-\hat{R}\left|\hat{\Lambda }\right|\hat{L}\left(W_L{}_{i,j+1/2}-W_R{}_{i,j+1/2}\right)\right]\end{array}$ (6)

这里，W_L、W_R代表通量所在的网格左右两侧的变量，F_L、F_R和G_L、G_R代表两侧变量形成的x、y方向通量。 $\hat{L}$ 、 $\hat{R}$ 、 $\hat{\Lambda }$ 则代表了Jacobi矩阵的左右特征向量和特征值对角矩阵的平均值。Jacobi矩阵为通量对变量的偏导数，即 $\partial F/\partial W$ 、 $\partial G/\partial W$ 。

2.3. 通量相关矩阵

对于左右两侧的变量及通量，表达形式如下：

$W_K=\left\{\begin{array}{c}{\rho }_K\\ {\rho }_K{u}_K\\ {\rho }_K{v}_K\\ {\rho }_K{E}_K\\ {\left(1/\Gamma \right)}_K\\ {\left(p_{ref}/\Gamma \right)}_K\\ {\left(\rho p_{ref}\right)}_K\\ {\left(\rho Y_{\text{I}}\right)}_K\end{array}\right\}$ ， $F_K或G_K=\left\{\begin{array}{c}{\left(\rho \theta \right)}_K\\ {\left(\rho \theta \right)}_K{u}_K+p_K{\zeta }_x\\ {\left(\rho \theta \right)}_K{v}_K+p_K{\zeta }_y\\ \left({\rho }_K{E}_K+p_K\right){\theta }_K\\ \theta {\left(1/\Gamma \right)}_K+\rho \varphi {\theta }_K\\ \theta {\left(p_{ref}/\Gamma \right)}_K+\rho \phi {\theta }_K\\ \theta {\left(\rho p_{ref}\right)}_K+\rho \psi {\theta }_K\\ {\left(\rho Y_I\right)}_K{\theta }_K\end{array}\right\}\left(K=L,R\right)$ (7)

这里，ζ_x和ζ_y的数值分别定义为：

${\zeta }_x=\{\begin{array}{l}1通量F\\ 0通量G\end{array},{\zeta }_y=\{\begin{array}{l}0通量F\\ 1通量G\end{array}$

其中 $\theta =u{\zeta }_x+v{\zeta }_y$ 。(7)中，未注明角标的参数θ、r、f、j、y则代表节点i，j处的数值。这样Jacobi矩阵A可以通过(7)式求偏导数得到：

$A=\left[\begin{array}{cccccccc}& {\zeta }_x& {\zeta }_y& & & & & \\ K{\zeta }_x-u\theta & \left(1-\Gamma \right)u{\zeta }_x+\theta & u{\zeta }_y-\Gamma v{\zeta }_x& \Gamma {\zeta }_x& -p\Gamma {\zeta }_x& \Gamma {\zeta }_x& -\Gamma {\zeta }_x& \\ K{\zeta }_y-v\theta & v{\zeta }_x-\Gamma u{\zeta }_y& \left(1-\Gamma \right)u{\zeta }_y+\theta & \Gamma {\zeta }_y& -p\Gamma {\zeta }_y& \Gamma {\zeta }_y& -\Gamma {\zeta }_y& \\ \left(K-H\right)\theta & H{\zeta }_x-\Gamma u\theta & H{\zeta }_y-\Gamma v\theta & \left(\Gamma +1\right)\theta & -p\Gamma \theta & \Gamma \theta & -\Gamma \theta & \\ -\varphi \theta & \varphi & & & \theta & & & \\ -\phi \theta & \phi & & & & \theta & & \\ -\psi \theta & \psi & & & & & \theta & \\ -Y_{\text{I}}\theta & Y_{\text{I}}& & & & & & \theta \end{array}\right]$ (8)

这里，H为熵： $H=E+p/\rho$ 。且有 $K=\Gamma \left(u^2+v^2\right)/2$ 。由矩阵A可以用偏微分关系求得特征值对角矩和左右特征向量矩阵：

$\Lambda =\left[\begin{array}{cccccccc}\theta -c& & & & & & & \\ & \theta & & & & & & \\ & & \theta & & & & & \\ & & & \theta +c& & & & \\ & & & & \theta & & & \\ & & & & & \theta & & \\ & & & & & & \theta & \\ & & & & & & & \theta \end{array}\right]$

这里c代表声速，计算式为：

$c=\sqrt{\Gamma \left(H-\frac{1}{2}\left(u^2+v^2\right)-p\varphi +\phi -\psi \right)}$ (9)

$L=\frac{\Gamma }{2c^2}\left[\begin{array}{cccccccc}\theta \xi +\frac{u^2+v^2}{2}& -u-{\zeta }_x\xi & -v-{\zeta }_y\xi & 1& -p& 1& -1& \\ -u^2-v^2+\kappa & 2u& 2v& -2& 2p& -2& 2& \\ \left({\zeta }_{y}u-{\zeta }_{x}v\right)\kappa & -{\zeta }_y\kappa & {\zeta }_x\kappa & & & & & \\ -\theta \xi +\frac{u^2+v^2}{2}& -u+{\zeta }_x\xi & -v+{\zeta }_y\xi & 1& -p& 1& -1& \\ -\varphi \left(u^2+v^2\right)& 2\varphi u& 2\varphi v& -2\varphi & 2\varphi p+\kappa & -2\varphi & 2\varphi & \\ -\phi \left(u^2+v^2\right)& 2\phi u& 2\phi v& -2\phi & 2\phi & -2\phi +\frac{\kappa }{\phi }& 2\phi & \\ -\psi \left(u^2+v^2\right)& 2\psi u& 2\psi v& -2\psi & 2\psi & -2\psi & 2\psi +\frac{\kappa }{\psi }& \\ -Y\left(u^2+v^2\right)& 2Yu& 2Yv& -2Y& 2Y& -2Y& 2Y& \kappa \end{array}\right]$

$R=\left[\begin{array}{cccccccc}1& 1& 0& 1& & & & \\ u-{\zeta }_{x}c& u& -{\zeta }_y& u+{\zeta }_{x}c& & & & \\ v-{\zeta }_{y}c& v& {\zeta }_x& v+{\zeta }_{y}c& & & & \\ H-\theta c& \frac{1}{2}\left(u^2+v^2\right)& -{\zeta }_{y}u+{\zeta }_{x}v& H+\theta c& p& -1& 1& \\ \varphi & & & \varphi & 1& & & \\ \phi & & & \phi & & 1& & \\ \psi & & & \psi & & & 1& \\ Y& & & Y& & & & 1\end{array}\right]$

这里 $k=2c^2/\Gamma$ ， $\xi =c/\Gamma$ 。

2.4. Roe平均值计算

在方程组(6)中， $\hat{L}$ 、 $\hat{R}$ 、 $\hat{\Lambda }$ 中的参数，需要根据左右两侧的状态取平均值。这里采用最为常用的一种Roe平均值，计算方式如下：

$\hat{u}=\frac{\sqrt{{\rho }_L}{u}_L+\sqrt{{\rho }_R}{u}_R}{\sqrt{{\rho }_L}+\sqrt{{\rho }_R}},\hat{v}=\frac{\sqrt{{\rho }_L}{v}_L+\sqrt{{\rho }_R}{v}_R}{\sqrt{{\rho }_L}+\sqrt{{\rho }_R}},\hat{H}=\frac{\sqrt{{\rho }_L}{H}_L+\sqrt{{\rho }_R}{H}_R}{\sqrt{{\rho }_L}+\sqrt{{\rho }_R}}$

原始的Roe格式未提供p和G的处理方法，这里采用如下计算方式：

$\frac{1}{\hat{\Gamma }}=\frac{\sqrt{{\rho }_L}\left(1/{\Gamma }_L\right)+\sqrt{{\rho }_R}\left(1/{\Gamma }_R\right)}{\sqrt{{\rho }_L}+\sqrt{{\rho }_R}},\frac{\hat{p}}{\hat{\Gamma }}=\frac{\sqrt{{\rho }_L}\left(p_L/{\Gamma }_L\right)+\sqrt{{\rho }_R}\left(p_R/{\Gamma }_R\right)}{\sqrt{{\rho }_L}+\sqrt{{\rho }_R}}$

参数f、j、y为节点处的数值，因此不需要对网格左右侧取平均值。声速c可根据(9)式完成求解。

3. 数值算例

这里再考虑一个钼和液态MORB(Mid-Ocean Ridge Basalt)相互作用的问题。初始时刻，整个流场计算域长宽都为1 m。MORB分布在[0.4, 0.6] × [0, 0.5]的一块方形区域，其余区域均为钼。左侧[0, 0.3 m]区域内的钼为高压态，除此以外都为正常态的钼。钼和液态MORB的物理特性均由Mie-Grüneisen状态方程(2)来表示，其中的参数为：

$\Gamma ={\Gamma }_0{\left(\frac{V}{V_0}\right)}^q,p_{ref}=p_0+\frac{c_0{}^2\left(V_0-V\right)}{{\left[V_0-s\left(V_0-V\right)\right]}^2},e_{ref}=e_0+\frac{1}{2}\left(p_{ref}+p_0\right)\left(V_0-V\right)$

这里V为相对体积，V = 1/r。流场中各介质的物理状态为：

$\begin{array}{l}\{\begin{array}{l}液态\text{MORB}:\rho =2.26\times {10}^3\text{kg}/{\text{m}}^{\text{3}},p=1\times {10}^5\text{pa},u=0,\\ 正常态钼:\rho =9.961\times {10}^3\text{kg}/{\text{m}}^{\text{3}},p=1\times {10}^5\text{pa},u=0\\ 压缩态钼:\rho =11.042\times {10}^3\text{kg}/{\text{m}}^{\text{3}},p=3\times {10}^{10}\text{pa},u=543\text{m}/\text{s}\end{array}\\ 液态\text{MORB}:{\rho }_0=2.26\times {10}^3\text{kg}/{\text{m}}^{\text{3}},c_0=2100\text{m}/\text{s},s=1.68,{\Gamma }_0=1.56,q=1.0\\ 钼:{\rho }_0=9.96\times {10}^3\text{kg}/{\text{m}}^{\text{3}},c_0=4770\text{m}/\text{s},s=1.43,{\Gamma }_0=0.18,q=1.0\end{array}$

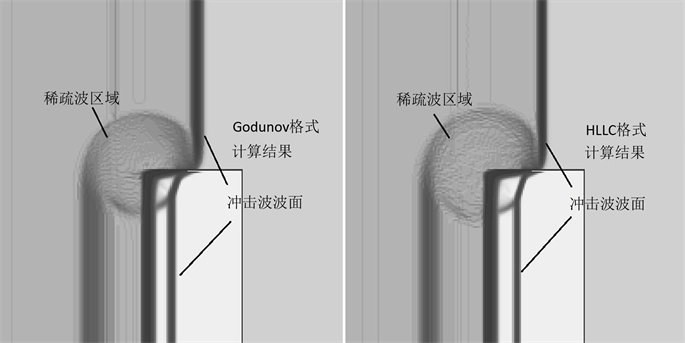
Figure 1. Density contours of Godunov scheme (left) and HLLC scheme (right)

图1. Godunov格式(左)和HLLC格式(右)的密度云图

Figure 2. Pressure contours of Godunov scheme (left) and HLLC scheme (right)

图2. Godunov格式(左)和HLLC格式(右)的压力云图

当高压态的钼以冲击波的形式向右推进时，上半部分没有受到其它介质的影响，一直沿直线传播；而下半部分冲击波冲击到MORB块上，与MORB块产生相互作用。图1和图2为50 μs时刻的密度与压力的分布状态。此时，一部分冲击波进入MORB块中继续传播，一部分返回钼中形成稀疏波。冲击波为强间断面，在图中可以观察到明显的波面。而稀疏波属于弱间断面，在图中则显示为大范围的密度变化。冲击波的波面与稀疏波的边界组合到一起，形成一个近似的圆形。

为了验证计算结果的准确性，本文将Godunov型格式的计算结果，与文献 [6] 中HLLC的计算结果进行了比较。比较的结果可以发现，无论是密度和压力，两者的计算结果均吻合的比较好。但是由于HLLC格式中，为了保证守恒方程与非守恒方程的波面运动速度一致，对差分格式上的进行了改动，这使得两种格式的计算结果中，冲击波波面的位置与稀疏波区域边界的位置出现了小幅度的差异。

4. 结论

本文针对Mie-Grüneisen多介质混合模型结构复杂、非线性强的特点，提供了Godunov型的计算格式。经过推导后的Godunov型格式，可以同时考虑到模型中的守恒与非守恒关系式，且求解过程不需要借助其它的数值手段。通过和其它格式的数值结果对比，证明Godunov型格式可以得到稳定无振荡的数值解。

基金项目

国家自然科学基金资助项目(11702066)；广东省自然科学基金(2017A030313275)；广东海洋大学“创新强校工程”省财政资金支持项目(GDOU2016050258, GDOU2017052623)。