一类中立型Markovian跳跃系统的渐近稳定性

Asymptotic Stability of a Class of Neutral Markovian Jump Systems

摘要: 稳定性是动力系统最重要的性质之一，对解决实际问题具有很重要的理论意义。而时滞的存在是系统性能变差和系统不稳定的根源，故引起国内外许多专家和学者对其进行研究。本文考虑了一类中立型Markovian跳跃系统的渐近稳定性问题。首先，构造李雅普诺夫函数，利用Ito’s引理和Jensen’s不等式，获得渐近稳定性的条件。其次，使用MATLAB中的LMI工具箱，验证结果的正确性。最后，列举两个实例，验证此方法的有效性。

Abstract: Stability is one of the most important properties of dynamical system, which has important theo-retical significance to solve practical problems. The existence of time-delays is the root of system performance difference and systematic instability, so it has been considered by many scientists and scholars at home and abroad. In this paper, the asymptotic stability of a class of neutral Markovian jump systems is considered. Firstly, the Lyapunov function is constructed and the conditions for asymptotic stability are obtained by using Ito’s lemma and Jensen’s inequality. Secondly, the LMI toolbox in MATLAB is used to verify the correctness of the results. Finally, two examples are given to verify the validity of the method.

1. 引言

中立型Markovian跳跃系统是一类特殊的切换系统，系统的切换规律由Markovian过程控制 [1] 。渐近稳定性是时滞系统中最重要的性质之一，近些年来，许多专家和学者分别对中立型系统、Markovian跳跃系统的渐近稳定性进行深入研究，且取得了丰硕的成果 [2] [3] [4] [5] [6] 。稳定性是系统受到外界干扰时，偏离其平衡状态，当干扰消失时，能否回到其平衡状态的动力学行为。对于研究系统的稳定性还有大量工作需要完成 [7] [8] [9] [10] 。

研究系统的稳定性，常用的方法有三种：劳斯判据、赫尔维茨判据、李雅普诺夫定理。中立型系统、Markovian跳跃系统的大多数稳定性结果是基于Lyapunov-Krasovskii (L-K)方法获得的 [11] [12] 。许多研究人员在李雅普诺夫定理的基础上，提出了各种技术来推导系统类别和时滞相关稳定性标准，例如模型转换技术、改进的边界技术和矩阵分析方法等 [10] [13] [14] [15] 。

本文考虑了一类具有时变时滞和分布时滞的中立型Markovian跳跃系统的渐近稳定性问题。构造李雅普诺夫函数，利用Ito’s引理和Jensen’s不等式分析技巧，获得渐近稳定性的条件。

2. 问题描述

首先，考虑以下具有时变时滞和分布时滞的中立型Markovian跳跃系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(r_t,t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)=A_{\left(r_t,t\right)}x\left(t\right)+B_{\left(r_t,t\right)}x\left(t-h\left(t\right)\right)+D_{\left(r_t,t\right)}{\displaystyle {\int }_{t-r}^{t}x\left(s\right)\text{d}s}\hfill \\ x\left(t_0+\theta \right)=0,\forall \theta \in \left[\rho ,0\right].\hfill \end{array}$ (1)

其中， $x\left(t\right)\in {\Re }^n$ 是状态向量， $\tau \left(t\right)$ 是离散时滞， $h\left(t\right)$ 是时变时滞，且满足以下不等式

$\begin{array}{l}0\le \tau \left(t\right)\le \tau ,0<\stackrel{\dot{}}{\tau }\left(t\right)\le {\mu }_1<1,\\ 0\le h_0\le h\left(t\right)\le h,0<\stackrel{\dot{}}{h}\left(t\right)\le {\mu }_2<1.\end{array}$ (2)

$A_{\left(r_t,t\right)},B_{\left(r_t,t\right)},C_{\left(r_t,t\right)}$ 和 $D_{\left(r_t,t\right)}\in {\Re }^{n\times n}$ 是已知含有状态转移概率的常数矩阵， $\left\{r_t\right\},t>0$ 在马尔科夫过程有限状态概率空间中 $\xi =\left\{1,2,3,\cdots ,N\right\}$ 取值，且有 $\Lambda =\left({\lambda }_{ij}\right)\left(i,j\in \xi \right)$ ，即

$P\left(r_{\left(t+\Delta \right)}=j|r_{\left(t\right)}=i\right)=\{\begin{array}{ll}{\lambda }_{ij}\Delta +o\left(\Delta \right),\hfill & i\ne j\hfill \\ 1+{\lambda }_{ii}\Delta +o\left(\Delta \right),\hfill & i=j\hfill \end{array}$ (3)

其中， $\Delta >0，\underset{△\to 0}{\lim }\frac{o\left(\Delta \right)}{\Delta }=0,{\lambda }_{ij}\ge 0$ ，对任意的 $i\ne j$ ， ${\lambda }_{ij}\ge 0$ 表示由t时刻的第i状态转移到 $t+\Delta$ 时刻的第j状态的概率，并且有 ${\lambda }_{ii}=-{\displaystyle \underset{j=1,j\ne i}{\overset{N}{\sum }}{\lambda }_{ij}}$ 。它们的状态转移概率矩阵为

$\Lambda =\left[\begin{array}{cccc}{\lambda }_{11}& ?& {\lambda }_{13}& {\lambda }_{14}\\ ?& {\lambda }_{22}& ?& ?\\ {\lambda }_{31}& ?& {\lambda }_{33}& {\lambda }_{34}\\ {\lambda }_{41}& ?& ?& ?\end{array}\right],$ (4)

其中 $?$ 表示未知的状态转移概率，对于任意的 $i\in \xi$ ，集合 $U^i$ 表示 $U^i=U_k^i\cup U_{uk}^i$ 其中

$U_k^i:=\left\{j:对于j\in \xi ,{\lambda }_{ij}已知\right\},$

$U_{uk}^i:=\left\{j:对于j\in \xi ,{\lambda }_{ij}已知\right\}.$

此外， $U_k^i$ 是一个非空集，可以表示为 $U_k^i=\left\{k_1^i,k_2^i,\cdots ,k_n^i\right\}$ ，其中 $1\le n\le N$ 为非负整数， $$ 表示状态转移概率矩阵 $\Lambda$ 中第i行第j列已知元素。

3. 定义及引理

定义1 [16] 如果对于任意的 $\delta$ 和 $x\left(0\right)=x_0\in R^n$ ，满足以下不等式

${\displaystyle {\int }_{t=0}^{\infty }E\left\{{\Vert x\left(t,x_0\right)\Vert }^{\delta }\right\}\text{d}t}<\infty$ (5)

则系统是渐近稳定的。

引理1 [17] 针对中立型马尔科夫跳跃系统(1)，若 $V\left(x_t,t>0,r_t=i\right)=V\left(x_t,t,i\right)$ ，Lyapunov函数满足以下等式

$LV\left(x_t,t,i\right)=\underset{\Delta \to 0^{+}}{\lim }\frac{1}{\Delta }\left[E\left\{V\left(x_{t+\Delta },t+\Delta ,r_{t+\Delta }\right)|x_t,r_t=i\right\}-V\left(x_t,t,i\right)\right]<0$ (6)

则系统(1)是稳定的。

引理2 [18] 假设 $h\in R^n$ 和 $x\left(t\right)\in R^n$ ，对于任意正定矩阵W有以下不等式成立

$-h{\displaystyle {\int }_{t-h}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)W\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le {\left[\begin{array}{c}x\left(t\right)\\ x\left(t-h\right)\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}-W& W\\ W& -W\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ x\left(t-h\right)\end{array}\right]$ (7)

引理3 [19] 对于任意正定矩阵 $S\in R^{n\times n}$ ，标量 $\alpha >\beta$ ，有以下不等式成立

$\left(\alpha -\beta \right){\displaystyle {\int }_{\beta }^{\alpha }{x}^{\text{T}}}\left(s\right)Sx\left(s\right)\text{d}s\ge \left({\displaystyle {\int }_{\beta }^{\alpha }{x}^{\text{T}}}\left(s\right)\text{d}s\right)S\left({\displaystyle {\int }_{\beta }^{\alpha }x}\left(s\right)\text{d}s\right)$ (8)

4. 主要结果

定理1 假如存在实对称矩阵 $P_i\in {\Re }^{n\times n}$ ，适当维数的实矩阵 $R_i,Q_i,W,S_1,S_2,S_3,O\in {\Re }^{n\times n}$ ，且 $M_1,M_2,M_3$ 是任意维的矩阵，则系统(1)渐近稳定。

$\Phi =\left[\begin{array}{ccccccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}& {\varphi }_{14}& W& {\varphi }_{16}& {\varphi }_{17}\\ \ast & {\varphi }_{22}& {\varphi }_{23}& {\varphi }_{24}& 0& 0& {\varphi }_{27}\\ \ast & \ast & {\varphi }_{33}& {\varphi }_{34}& 0& {\varphi }_{36}& 0\\ \ast & \ast & \ast & {\varphi }_{44}& 0& 0& {\varphi }_{47}\\ \ast & \ast & \ast & \ast & -W& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\varphi }_{66}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\varphi }_{77}\end{array}\right]<0$ (8)

$\begin{array}{l}{\displaystyle \underset{j=U_k^i}{\sum }{\lambda }_{ij}}\left(Q_j-Q_i\right)<0;{\displaystyle \underset{j=U_k^i}{\sum }{\lambda }_{ij}}\left(R_j-R_i\right)<0,\\ P_j-P_i\le 0,j\in U_{uk}^i,j\ne i;Q_j-Q_i\le 0,j\in U_{uk}^i,j\ne i;\\ Q_j-Q_i\ge 0,j\in U_k^i,j=i;R_j-R_i\le 0,j\in U_{uk}^i,j\ne i;\\ R_j-R_i\ge 0,j\in U_k^i,j=i.\end{array}$

其中

${\varphi }_{11}=P_i{A}_i+A_i^{\text{T}}{P}_i+Q_i+h{S}_1-\frac{1-{\mu }_2}{h}{S}_3-W-\left(\frac{h_0^4}{4}+h_0^2\right)T+rO+M_1{A}_i+{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}\left(P_j-P_i\right)$ ,

${\varphi }_{12}=h{S}_2-M_1+A_i^{\text{T}}{M}_2$ , ${\varphi }_{13}=P_i{B}_i+\frac{1-{\mu }_2}{h}{S}_3+M_1{B}_i$ ,

${\varphi }_{14}=P_i{C}_i+M_1{C}_i+A_i^{\text{T}}{M}_3$ , ${\varphi }_{16}=-\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}+h_0^{2}T$ ,

${\varphi }_{17}=P_i{D}_i+M_1{D}_i$ , ${\varphi }_{22}=R_i+{\tau }^{2}W-M_2$ , ${\varphi }_{23}=B_i^{\text{T}}{M}_2$ ,

${\varphi }_{24}=C_i^{\text{T}}{M}_2-M_3$ , ${\varphi }_{27}=D_i^{\text{T}}{M}_2$ , ${\varphi }_{33}=-\left(1-{\mu }_2\right)Q_i$ ,

${\varphi }_{34}=B_i^{\text{T}}{M}_3$ , ${\varphi }_{36}=\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}$ , ${\varphi }_{44}=-\left(1-{\mu }_1\right)R_i+2M_3{C}_i$ ,

${\varphi }_{47}=M_3{D}_i$ , ${\varphi }_{66}=-\frac{1-{\mu }_2}{h}{S}_1$ , ${\varphi }_{77}=-\frac{1}{r}O$ .

证明：构造李雅普诺夫函数

$V\left(x_t,t,r_t\right)={\displaystyle \underset{n=1}{\overset{7}{\sum }}{V}_n}\left(x_t,t,r_t\right)$ (9)

其中

$V_1\left(x_t,t,r_t\right)=x^{\text{T}}\left(t\right)P_{i}x(t)$

$V_2\left(x_t,t,r_t\right)={\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)Q_{i}x\left(s\right)\text{d}s}$

$V_3\left(x_t,t,r_t\right)={\displaystyle {\int }_{t-\tau \left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)R_i\stackrel{\dot{}}{x}\left(s\right)\text{d}s}$

$V_4\left(x_t,t,r_t\right)={\displaystyle {\int }_{t-h\left(t\right)}^t\left(h\left(t\right)-t+s\right){\xi }^{\text{T}}\left(s\right)S\xi \left(s\right)\text{d}s}$

$V_5\left(x_t,t,r_t\right)={\displaystyle {\int }_{-\tau \left(t\right)}^t{\displaystyle {\int }_{t+\theta }^t{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)\tau \left(t\right)W\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\theta }}$

$V_6\left(x_t,t,r_t\right)=\frac{h_0{}^2}{2}{\displaystyle {\int }_{-h_0}^0{\displaystyle {\int }_{\theta }^0{\displaystyle {\int }_{t+\lambda }^t{x}^{\text{T}}\left(s\right)Tx\left(s\right)\text{d}s\text{d}\theta \text{d}\lambda }}}$

$V_7\left(x_t,t,r_t\right)={\displaystyle {\int }_{-r}^t{\displaystyle {\int }_{t+\theta }^t{x}^{\text{T}}\left(s\right)Ox\left(s\right)\text{d}s\text{d}\theta }}$

注意： $\xi \left(t\right)={\left[\begin{array}{cc}{x}^{\text{T}}\left(t\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\end{array}\right]}^{\text{T}}$

由引理1可得

$\begin{array}{c}L{V}_1\left(x_t,t,i\right)=2x^{\text{T}}\left(t\right)P_i\stackrel{\dot{}}{x}\left(t\right)+x^{\text{T}}\left(t\right){\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{P}_{j}x\left(t\right)\\ =2x^{\text{T}}\left(t\right)P_i\left[A_{i}x\left(t\right)+B_{i}x\left(t-h\left(t\right)\right)+C_i\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)+D_i{\displaystyle {\int }_{t-r}^{t}x\left(s\right)\text{d}s}\right]+x^{\text{T}}\left(t\right){\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{P}_{j}x\left(t\right)\\ =x^{\text{T}}\left(t\right)\left[P_i{A}_i+A_i^{\text{T}}{P}_i\right]x\left(t\right)+2x^{\text{T}}\left(t\right)P_i{B}_{i}x\left(t-h\left(t\right)\right)+2x^{\text{T}}\left(t\right)P_i{C}_i\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)\\ +2x^{\text{T}}\left(t\right)P_i{D}_i{\displaystyle {\int }_{t-r}^{t}x\left(s\right)\text{d}s}+x^{\text{T}}\left(t\right){\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{P}_{j}x\left(t\right)\end{array}$ (10)

$\begin{array}{c}L{V}_2\left(x_t,t,i\right)=x^{\text{T}}\left(t\right)Q_{i}x\left(t\right)-\left(1-\stackrel{\dot{}}{h}\left(t\right)\right)x^{\text{T}}\left(t-h\left(t\right)\right)Q_{i}x\left(t-h\left(t\right)\right)+{\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{Q}_j\right)x\left(s\right)\text{d}s\\ \le x^{\text{T}}\left(t\right)Q_{i}x\left(t\right)-\left(1-{\mu }_2\right)x^{\text{T}}\left(t-h\left(t\right)\right)Q_{i}x\left(t-h\left(t\right)\right)+{\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{Q}_j\right)x\left(s\right)\text{d}s\end{array}$ (11)

$\begin{array}{c}L{V}_3\left(x_t,t,i\right)={\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)R_i\stackrel{\dot{}}{x}\left(t\right)-\left(1-\stackrel{\dot{}}{\tau }\left(t\right)\right){\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)R_i\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)+{\displaystyle {\int }_{t-\tau \left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{R}_j\right)x\left(s\right)\text{d}s\\ \le {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)R_i\stackrel{\dot{}}{x}\left(t\right)-\left(1-{\mu }_1\right){\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)R_i\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)+{\displaystyle {\int }_{t-\tau \left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{R}_j\right)x\left(s\right)\text{d}s\end{array}$ (12)

$\begin{array}{c}L{V}_4\left(x_t,t,i\right)=h\left(t\right){\xi }^{\text{T}}\left(t\right)S\xi \left(t\right)-\left(1-\stackrel{\dot{}}{h}\left(t\right)\right){\displaystyle {\int }_{t-h\left(t\right)}^t{\xi }^{\text{T}}\left(s\right)S\xi \left(s\right)\text{d}s}\\ \le h{\left[\begin{array}{c}x\left(t\right)\\ \stackrel{\dot{}}{x}\left(t\right)\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}{S}_1& S_2\\ S_2^{\text{T}}& S_3\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \stackrel{\dot{}}{x}\left(t\right)\end{array}\right]\\ -\frac{1-{\mu }_2}{h}{\left[{\displaystyle {\int }_{t-h\left(t\right)}^t\left(\begin{array}{c}x\left(s\right)\\ \stackrel{\dot{}}{x}\left(s\right)\end{array}\right)\text{d}s}\right]}^{\text{T}}\left[\begin{array}{cc}{S}_1& S_2\\ S_2^{\text{T}}& S_3\end{array}\right]\left[{\displaystyle {\int }_{t-h\left(t\right)}^t\left(\begin{array}{c}x\left(s\right)\\ \stackrel{\dot{}}{x}\left(s\right)\end{array}\right)\text{d}s}\right]\\ \le h{\left[\begin{array}{c}x\left(t\right)\\ \stackrel{\dot{}}{x}\left(t\right)\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}{S}_1& S_2\\ S_2^{\text{T}}& S_3\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \stackrel{\dot{}}{x}\left(t\right)\end{array}\right]\\ -\frac{1-{\mu }_2}{h}{\left[\begin{array}{c}{\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\\ x\left(t\right)-x\left(t-h\left(t\right)\right)\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}{S}_1& S_2\\ S_2^{\text{T}}& S_3\end{array}\right]\left[\begin{array}{c}{\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\\ x\left(t\right)-x\left(t-h\left(t\right)\right)\end{array}\right]\end{array}$

由引理3可得

$\begin{array}{c}L{V}_4\left(x_t,t,i\right)\le x{\left(t\right)}^{\text{T}}\left(h{S}_1-\frac{1-{\mu }_2}{h}{S}_3\right)x\left(t\right)+{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)h{S}_2^{\text{T}}x\left(t\right)+x{\left(t\right)}^{\text{T}}h{S}_2\stackrel{\dot{}}{x}\left(t\right)+{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)h{S}_3\stackrel{\dot{}}{x}\left(t\right)\\ -\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)\left(\frac{1-{\mu }_2}{h}{S}_1\right)\left({\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)-x{\left(t\right)}^{\text{T}}\left(\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}\right)\left({\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)\\ +x^{\text{T}}\left(t-h\left(t\right)\right)\left(\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}\right)\left({\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)-\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)\left(\frac{1-{\mu }_2}{h}{S}_2\right)x\left(t\right)\\ +\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)\left(\frac{1-{\mu }_2}{h}{S}_2\right)x\left(t-h\left(t\right)\right)+x^{\text{T}}\left(t\right)\left(\frac{1-{\mu }_2}{h}{S}_3\right)x\left(t-h\left(t\right)\right)\\ +x^{\text{T}}\left(t-h\left(t\right)\right)\left(\frac{1-{\mu }_2}{h}{S}_3\right)x\left(t\right)-x^{\text{T}}\left(t-h\left(t\right)\right)\left(\frac{1-{\mu }_2}{h}{S}_3\right)x\left(t-h\left(t\right)\right)\end{array}$ (14)

$L{V}_5\left(x_t,t,i\right)={\tau }^2\left(t\right){\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)W\stackrel{\dot{}}{x}\left(t\right)-{\displaystyle {\int }_{t-\tau \left(t\right)}^t{\stackrel{\dot{}}{x}}^{\text{T}}}\left(s\right)\tau W\stackrel{\dot{}}{x}\left(s\right)\text{d}s$

由引理2可得

$\begin{array}{c}L{V}_5\left(x_t,t,i\right)\le {\tau }^2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)W\stackrel{\dot{}}{x}\left(t\right)+\left[\begin{array}{cc}{x}^{\text{T}}\left(t\right)& x^{\text{T}}\left(t-\tau \left(t\right)\right)\end{array}\right]\left[\begin{array}{cc}-W& W\\ W& -W\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ x\left(t-\tau \left(t\right)\right)\end{array}\right]\\ ={\tau }^2{\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)W\stackrel{\dot{}}{x}\left(t\right)+x^{\text{T}}\left(t\right)\left(-W\right)x\left(t\right)+x^{\text{T}}\left(t-\tau \left(t\right)\right)Wx\left(t\right)\\ +x^{\text{T}}\left(t\right)Wx\left(t-\tau \left(t\right)\right)+x^{\text{T}}\left(t-\tau \left(t\right)\right)\left(-W\right)x\left(t-\tau \left(t\right)\right)\end{array}$ (15)

$\begin{array}{c}L{V}_6\left(x_t,t,i\right)=\frac{{\left(h_0^2\right)}^2}{4}{x}^{\text{T}}\left(t\right)Tx\left(t\right)-\frac{h_0^2}{2}{\displaystyle {\int }_{-{\tau }_0}^0{\displaystyle {\int }_{t+\theta }^t{x}^{\text{T}}\left(s\right)Tx\left(s\right)\text{d}s\text{d}\theta }}\\ \le \frac{h_0^4}{4}{x}^{\text{T}}\left(t\right)Tx\left(t\right)-\left[h_0{x}^{\text{T}}\left(t\right)-\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)T\left(h_{0}x\left(t\right)-{\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)\right]\\ \le x^{\text{T}}\left(t\right)\left(\frac{h_0^4}{4}T-h_0^{2}T\right)x\left(t\right)+x^{\text{T}}\left(t\right)\left(h_0^{2}T\right)\left({\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)\\ +\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)\left(h_0^{2}T\right)x\left(t\right)-\left({\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}\right)T\left({\displaystyle {\int }_{t-h\left(t\right)}^{t}x\left(s\right)\text{d}s}\right)\end{array}$ (16)

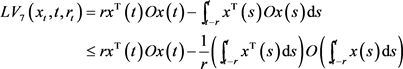(17)

对于任意矩阵 $M_1,M_2,M_3$ ，有以下等式成立

$\begin{array}{c}0=\left[\begin{array}{ccc}{x}^{\text{T}}\left(t\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)\end{array}\right]\left[\begin{array}{c}{M}_1\\ M_2\\ M_3\end{array}\right]\\ \times \left[-\stackrel{\dot{}}{x}\left(t\right)+A_{\left(r_t,t\right)}x\left(t\right)+B_{\left(r_t,t\right)}x\left(t-h\left(t\right)\right)+C_{\left(r_t,t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)+D_{\left(r_t,t\right)}{\displaystyle {\int }_{t-r}^{t}x\left(s\right)\text{d}s}\right]\end{array}$ (18)

由条件 $-{\displaystyle \underset{j=1,j\ne i}{\overset{N}{\sum }}{\lambda }_{ij}}=0$ ，有以下矩阵等式成立

$-x^{\text{T}}\left(t\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{P}_i\right)x\left(t\right)=0,\forall i\in \xi$ (19)

$-{\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{Q}_i\right)x\left(t\right)\text{d}s=0,\forall i\in \xi$ (20)

$-{\displaystyle {\int }_{t-\tau \left(t\right)}^t{x}^{\text{T}}}\left(s\right)\left({\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}{R}_i\right)x\left(t\right)\text{d}s=0,\forall i\in \xi$ (21)

由以上(10)~(21)可得

$\begin{array}{c}LV\left(x_t,t,i\right)={\displaystyle \underset{n=1}{\overset{7}{\sum }}L{V}_n\left(x_t,t,i\right)}\\ \le {\Psi }^{\text{T}}\left(t\right)\Phi \Psi \left(t\right)+x^{\text{T}}\left(t\right){\displaystyle \underset{j\in U_{uk}^i}{\sum }{\lambda }_{ij}}\left(P_j-P_i\right)x\left(s\right)+{\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}}\left(s\right){\displaystyle \underset{j\in U_k^i}{\sum }{\lambda }_{ij}}\left(Q_j-Q_i\right)x\left(s\right)\text{d}s\\ +{\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}}\left(s\right){\displaystyle \underset{j\in U_{uk}^i}{\sum }{\lambda }_{ij}}\left(Q_j-Q_i\right)x\left(s\right)\text{d}s+{\displaystyle {\int }_{t-\tau \left(t\right)}^t{x}^{\text{T}}}\left(s\right){\displaystyle \underset{j\in U_k^i}{\sum }{\lambda }_{ij}}\left(R_j-R_i\right)x\left(s\right)\text{d}s\\ +{\displaystyle {\int }_{t-\tau \left(t\right)}^t{x}^{\text{T}}}\left(s\right){\displaystyle \underset{j\in U_{uk}^i}{\sum }{\lambda }_{ij}}\left(R_j-R_i\right)x\left(s\right)\text{d}s\end{array}$

其中

${\Psi }^{\text{T}}\left(t\right)=\left[\begin{array}{cccc}{x}^{\text{T}}\left(t\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)& x^{\text{T}}\left(t-h\left(t\right)\right)& {\stackrel{\dot{}}{x}}^{\text{T}}\left(t-\tau \left(t\right)\right)\end{array}\begin{array}{ccc}{x}^{\text{T}}\left(t-\tau \left(t\right)\right)& {\displaystyle {\int }_{t-h\left(t\right)}^t{x}^{\text{T}}\left(s\right)\text{d}s}& {\displaystyle {\int }_{t-r}^t{x}^{\text{T}}\left(s\right)\text{d}s}\end{array}\right]$

所以有系统(1)的稳定条件 $LV\left(x_t,t,i\right)\le 0$ ，即

${\displaystyle {\int }_{t=0}^{\infty }E\left\{{\Vert x\left(t,x_0\right)\Vert }^{\delta }\right\}\text{d}t}<\infty$ (22)

则系统(1)是渐近稳定的。

其次，考虑以下具有时变时滞和分布时变时滞的中立型Markovian跳跃系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(r_t,t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)=A_{\left(r_t,t\right)}x\left(t\right)+B_{\left(r_t,t\right)}x\left(t-h\left(t\right)\right)+D_{\left(r_t,t\right)}{\displaystyle {\int }_{t-r\left(t\right)}^{t}x\left(s\right)\text{d}s},\hfill \\ x\left(t_0+\theta \right)=0,\forall \theta \in \left[0,\rho \right].\hfill \end{array}$ (23)

推论1 假如存在实对称矩阵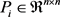，适当维数的实矩阵 $R_i,Q_i,W,S_1,S_2,S_3,O\in {\Re }^{n\times n}$ ，且 $M_1,M_2,M_3$ 是任意维的矩阵，则系统(23)渐近稳定。

$\tilde{\Phi }=\left[\begin{array}{ccccccc}{\tilde{\varphi }}_{11}& {\tilde{\varphi }}_{12}& {\tilde{\varphi }}_{13}& {\tilde{\varphi }}_{14}& W& {\tilde{\varphi }}_{16}& {\tilde{\varphi }}_{17}\\ \ast & {\tilde{\varphi }}_{22}& {\tilde{\varphi }}_{23}& {\tilde{\varphi }}_{24}& 0& 0& {\tilde{\varphi }}_{27}\\ \ast & \ast & {\tilde{\varphi }}_{33}& {\tilde{\varphi }}_{34}& 0& {\tilde{\varphi }}_{36}& 0\\ \ast & \ast & \ast & {\tilde{\varphi }}_{44}& 0& 0& {\tilde{\varphi }}_{47}\\ \ast & \ast & \ast & \ast & -W& 0& 0\\ \ast & \ast & \ast & \ast & \ast & {\tilde{\varphi }}_{66}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\tilde{\varphi }}_{77}\end{array}\right]<0$ (24)

$\begin{array}{l}{\displaystyle \underset{j=U_k^i}{\sum }{\lambda }_{ij}}\left(Q_j-Q_i\right)<0;{\displaystyle \underset{j=U_k^i}{\sum }{\lambda }_{ij}}\left(R_j-R_i\right)<0,\\ P_j-P_i\le 0,j\in U_{uk}^i,j\ne i;Q_j-Q_i\le 0,j\in U_{uk}^i,j\ne i;\\ Q_j-Q_i\ge 0,j\in U_k^i,j=i;R_j-R_i\le 0,j\in U_{uk}^i,j\ne i;\\ R_j-R_i\ge 0,j\in U_k^i,j=i.\end{array}$

其中

${\tilde{\varphi }}_{11}=P_i{A}_i+A_i^{\text{T}}{P}_i+Q_i+h{S}_1-\frac{1-{\mu }_2}{h}{S}_3-W-\left(\frac{h_0^4}{4}+h_0^2\right)T+rO+M_1{A}_i+{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\lambda }_{ij}}\left(P_j-P_i\right)$

${\tilde{\varphi }}_{12}=h{S}_2-M_1+A_i^{\text{T}}{M}_2$ , ${\tilde{\varphi }}_{13}=P_i{B}_i+\frac{1-{\mu }_2}{h}{S}_3+M_1{B}_i$ , ${\tilde{\varphi }}_{14}=P_i{C}_i+M_1{C}_i+A_i^{\text{T}}{M}_3$ ,

${\tilde{\varphi }}_{16}=-\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}+h_0^{2}T$ , ${\tilde{\varphi }}_{17}=P_i{D}_i+M_1{D}_i$ , ${\tilde{\varphi }}_{22}=R_i+{\tau }^{2}W-M_2$ , ${\tilde{\varphi }}_{23}=B_i^{\text{T}}{M}_2$ , ${\tilde{\varphi }}_{24}=C_i^{\text{T}}{M}_2-M_3$ , ${\tilde{\varphi }}_{27}=D_i^{\text{T}}{M}_2$ , ${\tilde{\varphi }}_{33}=-\left(1-{\mu }_2\right)Q$ , ${\tilde{\varphi }}_{34}=B_i^{\text{T}}{M}_3$ , ${\tilde{\varphi }}_{36}=\frac{1-{\mu }_2}{h}{S}_2^{\text{T}}$ , ${\tilde{\varphi }}_{44}=-\left(1-{\mu }_1\right)R+2M_3{C}_i$ , ${\tilde{\varphi }}_{47}=M_3{D}_i$ , ${\tilde{\varphi }}_{66}=-\frac{1-{\mu }_2}{h}{S}_1$ , ${\tilde{\varphi }}_{77}=-\frac{1-{\mu }_3}{r}O$ .

证明：推论1的证明过程和定理1类似，但需注意系统(23)含有时变时滞和分布时变时滞，此时分布时变时滞 $r\left(t\right)$ 需满足以下不等式

$0\le r\left(t\right)\le \tau ,0<\stackrel{\dot{}}{r}\left(t\right)\le {\mu }_3<1.$

即(17)式变为

$\begin{array}{c}\tilde{L}{V}_7\left(x_t,t,r_t\right)=r\left(t\right)x^{\text{T}}\left(t\right)Ox\left(t\right)-{\displaystyle {\int }_{t-r\left(t\right)}^t{x}^{\text{T}}}\left(s\right)Ox\left(s\right)\text{d}s\\ =r\left(t\right)x^{\text{T}}\left(t\right)Ox\left(t\right)-\frac{1-\stackrel{\dot{}}{r}\left(t\right)}{r\left(t\right)}\left({\displaystyle {\int }_{t-r\left(t\right)}^t{x}^{\text{T}}}\left(s\right)\text{d}s\right)O\left({\displaystyle {\int }_{t-r\left(t\right)}^{t}x}\left(s\right)\text{d}s\right)\\ \le r{x}^{\text{T}}\left(t\right)Ox\left(t\right)-\frac{1-{\mu }_3}{r}\left({\displaystyle {\int }_{t-r\left(t\right)}^t{x}^{\text{T}}}\left(s\right)\text{d}s\right)O\left({\displaystyle {\int }_{t-r\left(t\right)}^{t}x}\left(s\right)\text{d}s\right)\end{array}$ (25)

5. 仿真算例

例1 考虑以下具有时变时滞和分布时滞的中立型Markovian跳跃系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(r_t,t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)=A_{\left(r_t,t\right)}x\left(t\right)+B_{\left(r_t,t\right)}x\left(t-h\left(t\right)\right)+D_{\left(r_t,t\right)}{\displaystyle {\int }_{t-r}^{t}x\left(s\right)\text{d}s},\hfill \\ x\left(t_0+\theta \right)=0,\forall \theta \in \left[\rho ,0\right].\hfill \end{array}$

$A_1=\left[\begin{array}{cc}-1.2& 0.1\\ -0.1& -1\end{array}\right]$ , $A_2=\left[\begin{array}{cc}-1.2& 0.15\\ 0.1& -1.5\end{array}\right]$ , $B_1=\left[\begin{array}{cc}-0.6& 0.7\\ -1& -0.8\end{array}\right]$ , $B_2=\left[\begin{array}{cc}-0.15& 1.5\\ -1& -0.8\end{array}\right]$ ,

$C_1=C_2=\left[\begin{array}{cc}c& 0\\ 0& c\end{array}\right]$ , $$ , $D_2=\left[\begin{array}{cc}0.15& -1\\ -1& 0\end{array}\right]$ ,

假设

$h=0.1,\tau =0.1,{\mu }_1=0.75,{\mu }_2=0.5,r=0.75,h_0=\mathrm{0.1.}$

在这里，我们的目的是使用matlab中的LMI工具箱验证定理1中结果的有效性，假设初始状态 $x_0={\left[\begin{array}{cc}-1.8& 1.4\end{array}\right]}^{\text{T}}$ ，可得系统(1)的状态轨迹图(见图1)。

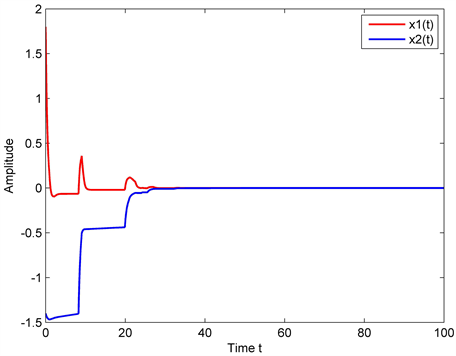
Figure 1. The state trajectory of a neutral Markovian jump system with time-varying delay and distributed delay

图1. 具有时变时滞和分布时变时滞的中立型Markovian跳跃系统状态轨迹图

例2 考虑以下具有时变时滞和分布时变时滞的中立型Markovian跳跃系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)-C_{\left(r_t,t\right)}\stackrel{\dot{}}{x}\left(t-\tau \left(t\right)\right)=A_{\left(r_t,t\right)}x\left(t\right)+B_{\left(r_t,t\right)}x\left(t-h\left(t\right)\right)+D_{\left(r_t,t\right)}{\displaystyle {\int }_{t-r\left(t\right)}^{t}x\left(s\right)\text{d}s},\hfill \\ x\left(t_0+\theta \right)=0,\forall \theta \in \left[0,\rho \right].\hfill \end{array}$

$A_1=\left[\begin{array}{cc}-2& 1\\ 1& -0.9\end{array}\right]$ , $B_1=\left[\begin{array}{cc}-1& -0.2\\ 1& 2\end{array}\right]$ , $C_1=\left[\begin{array}{cc}-1& -2\\ -1& 2\end{array}\right]$ , $D_1=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$ ,

$A_2=\left[\begin{array}{cc}-1& 1.5\\ 0& 1\end{array}\right]$ , $B_2=\left[\begin{array}{cc}2.5& 0\\ 0& 1\end{array}\right]$ , $C_2=\left[\begin{array}{cc}0.15& 0\\ -1& 0\end{array}\right]$ , $D_2=\left[\begin{array}{cc}0.15& -1\\ -1& 0\end{array}\right]$ .

假设

$h=0.1,\tau =0.1,{\mu }_1=0.75,{\mu }_2=0.5,r=0.75,h_0=0.1,{\mu }_3\text{=}\mathrm{0.75.}$

在这里，我们的目的是使用MATLAB中的LMI工具箱验证推论1中结果的有效性，假设初始状态 $x_0={\left[\begin{array}{cc}-2.0& 0.5\end{array}\right]}^{\text{T}}$ ，可得系统的状态轨迹图(见图2)。

Figure 2. The state trajectory of a neutral Markov jumping system with time-varying delay and time-varying distributed delay

图2. 具有时变时滞和分布时变时滞的中立型Markovian跳跃系统状态轨迹图

6. 总结

本文考虑了一类中立型Markovian跳跃系统的渐近稳定性问题。首先，构造李雅普诺夫函数，运用Ito’s引理和Jensen’s不等式分析技巧，获得系统渐近稳定的条件。其次，使用MATLAB中的LMI工具箱，验证结果的正确性。最后，列举两个实例，得到此方法的有效性。

基金项目

贵州省科技厅科学研究基金(J[2015]2074)，贵州省科技厅、贵州民族大学联合基金项目(LKM[2013]21)，贵州省教育厅群体创新研究项目贵州民族大学博士启动基金项目(KY[2016]021)，贵州民族大学科研基金资助项目(2017YB066)。

NOTES

^*通讯作者。