1. 引言
经典的1-倾斜模和倾斜代数是倾斜理论的两个基本的研究对象。前者是由Brenner和Buttler在 [1] 中提出的;后者作为遗传代数上1-倾斜模的自同态代数是由Happel和Ringel在 [2] 中引入的。对于任一个正整数m,Miyashita在 [3] 中将1-倾斜模的概念推广到m-倾斜模。众所周知,倾斜模和倾斜代数在代数表示论中起到十分重要的作用,研究诸如代数扩张等具有一定联系的两个代数间的倾斜不变性一直为人们所关注 [4] [5] [6] 。
设A是一个有限维K-代数,F是一个MaLand意义下 [7] [8] 的可分K-扩张,则
是A的一类重要的代数扩张。Passman [6] 证明了
既是A的优化扩张还是A的Frobienus扩张。因而,
和A之间的不变性质一直是人们重要研究对象。诸如表示型,整体维数,Gorenstein-整体维数等等都在
和A之间保持不变 [5] [6] [8] 。南京大学黄兆泳教授和本文作者在 [4] 中证明了二者具有相同的有限维数和表示维数。从 [4] 中可知
是遗传代数当且仅当A是遗传代数。而遗传代数恰好是一类重要的倾斜代数。一个自然的问题就是:如果
和A中有一个是倾斜代数,那么另一个是否为倾斜代数?本文给出了一个完整的回答。本文的主要定理
定理1.1:设K是一个代数封闭域,A是一个有限维K-代数,F是一个可分K-扩张。则A是倾斜代数当且仅当
是倾斜代数。
2. 预备知识
本文中的所有代数都是有限维K-代数,其中K是一个代数封闭域,所有模都是有限生成右模。设A有限维K-代数,将所有有限生成的A-模构成的范畴记为mod A。记pdAT和addAT分别为A-模T的投射维数和A-模T有限直和的直和项,记gl.dim A为A的整体维数。
设A是一个有限维K-代数,F是一个可分K-扩张。因为
既是A的优化扩张还是A的Frobienus 扩张,我们有以下结论。
引理2.1:设A是一个有限维K-代数,F是一个可分K-扩张。
1) 对于任一个
-模M,则M是
-模
的直和项;
2) 对于任一个
-模N,有
;
3) 如果I是内射A-模,则
是内射
-模;
4)
。
定义2.2 [3] :有限生成A-模T称为m-倾斜模,如果
1)
;
2) 对于任意正整数i,都有
;
3) mod A中存在长正合列:
。
定义2.3 [2] :有限维代数A称为倾斜代数,如果存在遗传代数B上的1-倾斜模T,使得
。
不难证明有限维A是倾斜代数当且仅当存在一个自同态代数为遗传代数的1-倾斜A-模。
设
是加法范畴,
为由
到AB (Abel群范畴)的所有反变函子组成的范畴。称函子
是凝聚函子,如果
中存在正合列:
,
,
。我们将
中所有凝聚函子组成的子范畴记为
。由Yoneda’s引理,
的投射对象是
中的形如
,
的函子。
的整体维数定义为所有凝聚函子的投射维数的上确界。下面的引理给出了自同态代数的整体维数和凝聚函子范畴的整体维数之间的联系。
引理2.4 [9] :设A是有限维K-代数,M是有限生成A-模。则
。
3. 主要结果
引理3.1:设K是一个域,A是一个有限维K-代数,F是K上的一个可分域扩张,M是一个
模,m是正整数。则
1) 如果X是m-倾斜A-模,则
是m-倾斜
-模。
2) 如果Y是m-倾斜A-模,则Y是m-倾斜
-模。
证明:首先,由( [4] ,引理3.5)得
是有限维K-代数。
1) 由m-倾斜代数的定义,结论显然成立。
2) 设
。
我们先证明必要性。
a) 设M是一个m-倾斜
-模,则由引理2.1可得
。
b) 设I是
的一个内射分解,则对于任意正整数i,则我们有以下同构
。
因为对于任意正整数i,
,故
。
c) 由m-倾斜模的定义可得
正合列
,
其中,所有
。显然,上面的正合列也是mod A中的正合列。
因为A是A-模
的直和项,我们有正合列:
。
其中,
。
综合a),b),c),由m-倾斜模的定义可知,Y是一个m-倾斜A-模。
再证充分性。假设Y是一个m-倾斜A-模。因为
,由引理2.1可得
。
对于任意正整数i,因为
,所以
根据m-倾斜模的定义,我们有正合列
其中,
。
用正变函子-⊗KF到上述正合列中,可得
中的正合列
。
另一方面,因为
,我们有
-双模同构
。
从而可得
-模同构
因此,
。从而可得Y是一个m-倾斜
-模。
下面的引理在本文的主要定理的证明中起到十分重要的作用,并且引理本身也是一个十分有趣的结论。
引理3.2:设A是Artin代数,T是有限生成的A-模,使得
。则
当且仅当addAT对子模封闭。
证明:先证必要性。要证addAT对子模封闭,只需证明T的有限直和的任意子模仍在addAT中。设M为Tt的任一个子模,其中t是正整数,
是嵌入映射。则范畴((addAT)op,Ab)中存在一个正合列:
,
其中
。由( [9] ,引理1.3)可得
。因此,
。由题设和引理2.4可得
。
因此,
是范畴
的投射对象。从而,由Yoneda’s引理得
。
下证必要性。对于任意
,mod A中存在态射
,使得
在
中正合。
令
,
,由题设可得
。
因为
,故正合列
可裂。
因此,序列
在
中正合。由此得到
上的正合列:
从而
。由引理2.4可得
。
定理3.3:设A有限维K-代数,F是K的有限域扩张。则A是倾斜代数当且仅当
是倾斜代数。
证明:先证必要性。因为A是倾斜代数,则存在1-倾斜A-模T,使得EndAT是遗传代数。
由引理3.1可知,
是1-倾斜
-模。
因为
,由引理2.1可得
。由倾斜代数的定义可知
是倾斜模。
再证充分性。设
是一个倾斜代数,则存在1-倾斜
-模X,使得
是一个遗传代数,从而
对子模封闭。又由引理3.1可得X是一个1-倾斜A-模。
以下证明XA对子模封闭。设N是
的任一个子模,其中
为自然数,则
与
的一个子模同构。由
-模同构
可得
,故
。又由引理2.1可得
为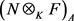 的直和项,从而,我们有
。
的直和项,从而,我们有
。
由引理3.2可得,
是一个遗传代数。因此,A是一个倾斜代数。
基金项目
此项研究受国家自然科学基金资助项目(11601304)和商丘师范学院校级青年骨干教师资助项目(2015GGJS04)资助。