1. 引言
本篇文章中所有的图都限定为无向的简单图。相关的术语和符号可以参考文献 [1] 。设
是一个简单图,其中
是图G的顶点集,
是图G的边集,我们分别用
和
记作
和
的阶。通常我们用
表示阶为n的路。对于
中的每一个点v,用
表示与点v相邻的所有顶点的集合,称为v的邻点集。
称为点v的度数。一般地,我们用
表示H是图G的一个子图或者表示H同构于G中的一个子图。
在一个连通图G中,记
为G中任意两个点
和v之间的距离(两点之间最短路的长度),
为图G的Wiener指标,定义为
。
这个概念最初是由Harry Wiener在文献 [2] 中提到的。从那时起,许多研究者对Wiener指标进行了广泛的研究。关于一些Wiener指标的化学应用和数学研究的调查可以参考文献 [3] [4] 以及其中引用的参考资料。
为图G的线图,其中
并且对于任意两个点在
中相邻当且仅当这两个点对应的边在G中相邻。
为图G的补图,其中
并且对于任意两个点u和v在
中相邻当且仅当u和v在G中不相邻。在文献 [5] 中Chartrand等研究者称线图的补图为跳图,记作
并且给出了
一些跳图是哈密顿的充分条件。吴和孟在文献 [6] 中给出了一些哈密顿跳图的结构。我们可以在文献 [7] [8] [9] [10] 中查阅到线图的补图的更多结果。
在文献 [5] 中Chartrand等研究者证明了如果一个跳图
是连通的,则它的直径不超过4。在文献 [2] 中吴和郭给出了跳图的直径r在1到4之间的原图G的结构。在本文中,我们将根据吴和郭的结果确定连通的跳图
的Wiener指标。
2. 主要内容
2.1. 预备知识
在文献 [5] 中Chartrand等人给出了下面的结果。
定理2.1.1 [5] 如果
是连通的,则
。
在文献 [2] 中吴和郭根据上面的结果给出了下面的定理。
定理2.1.2 [2] 对于一个边数不小于1的图G,如果
是连通的,则:
1)
当且仅当
;
2)
当且仅当:
a) G包含一个子图
,
是由给
中的点u加一个新的邻点,
b) 如果G中存在一条边关联v或x,则这条边必须是vx。此外,如果
,则
,
c) G中任意一条除
以外的边都与u关联;
3)
当且仅当:
a) G包含
,
b) 对于G中任意一条不在
上的边必有一个端点在
的2度顶点上,
c) 同时G不满足(2)中的情况;
4)
,其他。
在本文,我们主要根据上面对线图的补图的刻画来计算线图的补图的Wiener指标。
2.2. 直径小于等于2
引理2.2.1 如果
,
,
,则
。
证明:因为
,所以对于任意的点
,u和v之间的距离为1或2。因此
.
定理2.2.2对于一个边数为m的图G,如果
,则
证明:因为
,所以
,
其中
。
所以由引理2.2.1知:
.
2.3. 直径等于3
由定理2.1.2知:当
,则图G的结构如图1所示。
令
和
分别作为
的顶点集和边集,且
,
。假设
,
,
并且
,
,
,显然
,
,
。
定理2.3.1对于一个边数为m的图G,如果
,则
,
其中
且
。
证明:首先
。
如果
,对于任意边
且
,则在
中
到
,
,
,
的距离之和为6。令
且
。有
,
其中
。
现在我们来计算
:
对于任意边
和
其中
,则
。因此
.
对于任意边
,则
。因此
.
对于任意边
,则
。因此
.
对于任意边
,则
。因此
.
综上所述:
.
因此
.
2.4. 直径等于4
由定理2.1.2知:当
,G有三种结构形式
和
,如图2所示。
,
.
,
.
,
.
定理2.4.1 对于一个点数为n的图G,如果
,则
证明:对于任意图G,如果
,则对于任意边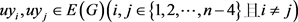 ,有
。因此
,有
。因此
.
对于任意边
,则
。因此
.
对于任意边
,显然
。因此
.
同理,
,
,
,
。
综上所述:
.
根据上面的方法我们得到,若
或
,有
基金项目
国家自然科学基金青年科学基金(NO. 11801487)。