1. 引言
很多前人对电脑涉及几何造型方面或者几何设计方面的两类问题进行了广泛的研究,发现曲面拼接问题在其当中的运用是非常的普遍。如Warren提出基于理想生成元的方法 [1] ,Wallner和Hottmann [2] 得到了二次曲面之间的有理拼接曲面,Groebner基方法 [3] 和吴文俊提出的特征列方法 [4] 使得交换代数及代数几何中的许多结果变成可计算的。Hartmann [5] 在构造了一个函数光滑拼接管道轴线的基础上,光滑拼接了两个圆管道,而在拼接粗细不同的管道拼接时,对于轴线光滑度有更高的要求。在计算几何领域针对怎样光滑拼接轴线异面的管道这一基础难点问题,到目前为止成功的研究成果相对来说甚少。雷娜 [6] 把两个已知的圆管道(其轴线为彼此异面)分成两段式成功地完成了光滑的三次拼接,其应用的方法是圆柱的辅助,并且借助了吴文俊公式。白根柱利用伍铁如 [7] 提出的曲面通过截平面展开的标准表达式的方法研究了两个轴线异面柱面沿着垂直截口光滑拼接问题 [8] ,得到了三次拼接曲面存在的充分必要条件,而且给出了三次曲面的光滑拼接存在时两个轴线异面的隐式代数曲面的系数所满足的条件。之后,我们提出了基于轴线光滑拼接的轴线异面管道光滑拼接方法,在文 [9] 中构造了以空间Bézier曲线为轴线的管道光滑拼接了两个轴线异面的管道,称之为广义Bézier管道,我们还可以构造以空间Bézier曲线为轴线的圆管道光滑拼接两个轴线异面的圆管道,在文 [10] 中构造了以带有形状参数
的Bézier曲线为轴线的圆管道光滑拼接两个轴线异面的粗细相同的圆管道。本文进一步研究以带有形状参数
的Bézier曲线为轴线的圆管道光滑拼接两个轴线异面的粗细不相同的圆管道。
定义1 [11] 给定四个控制顶点
,对任意
,
,构造一支三次Bézier曲线
其中的基函数为如下一个三次多项式
而
分别为形状参数。
由于(附加有2个形状参数的) Bézier曲线可以调控少数控制点旁边的曲线的形状,为了两个轴线异面且粗细不同的圆管道完成很好的光滑拼接,来构造了此曲线为轴线的圆管道。
2. 构造基于轴线光滑拼接的轴线异面管道的光滑拼接管道
设
和
是两个轴线异面的圆管道的参数表示,其中
是两个轴线异面的粗细不同的圆管道的半径,
,
分别是
和
时的法矢和副法矢。
和
是两个圆管道的轴线,分别位于
平面上和位于
平面上与
轴相交。
设
是
上不同的两个点,
是
上不同的两个点,把
当作控制顶点可以构造由带有形状参数
的三次Bézier曲线与之对应的一个特征多边形。那么根据相应的定义,得到一种三次空间Bézier曲线,两个轴线异面的粗细不同的圆管道可以借助于此曲线来完成轴线的光滑拼接。其参数表示为
我们再构造光滑拼接两个轴线异面的粗细不同的圆管道的某一母线的带有形状参数
的如下一支三次空间Bézier曲线
其中
是四个光滑拼接彼此轴线异面并且粗细不同圆管道母线的控制多边形的顶点。
于是,我们得以构造一拼接管道,使得有着异面轴线和不同半径的圆管道在里面完成拼接光滑。其参数表示为
其中
是一支三次Bézier曲线,其能光滑拼接两个轴线异面粗细不同的管道的轴线,并且带有
,
形状参数。而
是另一支光滑拼接两个轴线异面而且不同粗细的圆管道的某一母线的带有形状参数
的三次Bézier曲线
,
表示欧几里得范数。
3. 拼接实例
例1:两个管道,设轴线异面,其参数表示为
和
其中
分别为两个轴线异面的粗细不同圆管道的半径,在
和
时其法矢为
,其副法矢为
。取
,分别为带有两个形状参数
,
的Bézier曲线的四个控制顶点,当
时,两个异面轴线拼接光滑的参数表示为
构造一支光滑拼接两个轴线相互异面、粗细不同的圆管道的某一母线的带形状参数
的三次空间Bézier曲线
其中
分别为带有形状参数
和
的粗细不同的管道光滑拼接某两个母线的三次Bézier曲线的四个控制顶点。则两个管道(轴线异面并且粗细不同)进行光滑拼接的拼接管道的参数表示为
其中
和
分别为拼接管道在点
处的法矢和副法矢,
,
表示欧几里得范数。
其拼接效果图,如图1。
例2:有两个管道,设轴线异面,其参数表示为
和
其中
轴线异面粗细不同圆管道的半径,在
和
时,
是法矢,
是副法矢。而Bézier曲线(带有两个
和
形状参数)的四个控制顶点分别为
,
,
,
,当
时,两个异面的轴线拼接光滑的参数表示为

Figure 1. The blending of tubes with non-coplanar axes when the axes are vertical
图1. 轴线异面管道的轴线异面角为垂直的情形
构造一支三次空间Bézier曲线(带形状参数
和
、能光滑拼接两个轴线相互异面、粗细不同的圆管道的某一母线)
其中
,
分别是光滑拼接轴线相互
异面、粗细不同管道的某个母线的(带有两个形状参数
的) Bézier曲线的四个控制顶点,则两个(粗细不相同而且轴线相互异面)管道达到光滑地拼接,其拼接管道的参数表示为
则在点
处
是拼接管道的法矢,而
是拼接管道的副法矢,
,
表示欧几里得范数。
其拼接效果图,如图2。
4. 结束语
本文借助于一种带有形状参数
的三次Bézier曲线,利用它能够调控其控制顶点周围的曲线形
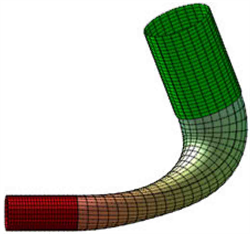
Figure 2. The blending of tubes with non-coplanar axes when the axes are non-vertical
图2. 轴线异面管道的轴线异面角不垂直的情形
状的这一特性,在轴线异面的两个管道的轴线能够光滑地拼接的基础上,轴线异面半径不同的两个管道的拼接光滑得以实现,进而得到了一个拼接管道使得轴线异面粗细不同的管道在其中能够光滑地拼接。在构造这个拼接管道实现光滑拼接过程中,只是利用把带有形状参数
和
的三次Bézier曲线来当作轴线的这一种媒介管道,进而构造出了一种光滑拼接两个轴线异面的管道。不同的管道完成光滑拼接可以借助于各种不相同的媒介来构造出不相同的光滑拼接管道。因此,两个轴线异面的管道完成拼接光滑可以借助于更多的媒介(即空间曲线)来构造得以实现,从而满足不同的用途。
基金项目
国家自然科学基金项目资助(11561052)。