1. 引言
生物趋化性为生物种群在某种特定的生物环境中在化学信号物质的影响下做定向运动,关于生物趋化性的研究对生物学领域有很重要的意义。在现实生活中运用也很广泛,如生物除污、伤口的愈合等等。最早的生物趋化模型是由Patlak和Keller-Segel提出,最简单的K-S趋化模型 [1] 如下
(1.1)
其中
表示一个光滑有界区域,
表示细胞的种群密度,
表示化学物质的浓度,
表示趋化敏感系数,
表示趋化灵敏度,体现趋化模型最本质的一项。数学家最注重研究趋化模型解的性态是否具有坍塌行为,即模型解在有限时间内或无限时间内是否爆破,此类问题的研究已经有了许多成果。当
时,Yagi等人证明了此模型解全局存在,不存在坍塌现象 [2] 。当
时,存在临界常数
,Nagai和Senba证明了如果初值满足
时,则此模型解存在且一致有界 [3] ,Horstmann和Wang证明了如果初值满足
,则此模型解在有限时间内或无限时间内发生爆破 [4] 。进一步,Nagai证明了满足
时,此模型经典解也在有限时间内发生爆破 [5] 。当
时,Winkler在文献 [6] 中证明了若对于任意的
,存在
使得
和
成立,此模型解存在且一致有界,而当初值满足
时,文献 [7] 利用Lyapunov泛函证明了此模型解会在有限时间内存在坍塌现象。
受文献 [8] [9] 工作的启发,本文研究具有间接信号产出的带有一般的趋化敏感函数的趋化模型,具体模型如下:
(1.2)
其中 是一个光滑有界区域,
表示飞行的山地松甲虫的种群密度,
表示做窝的山地松甲虫的种群密度,
表示化学信号的浓度。当
且
时,王笑丹等人在文献 [10] 中证明了模型解全局存在且一致有界。当
且
,logistic源项为
时,Li和Tao证明了模型解全局存在且一致有界 [11] 。但是当
,此模型的解的性态不明确。本文,主要考虑一般的趋化敏感函数情况,假设趋化敏感函数
和函数
满足
是一个光滑有界区域,
表示飞行的山地松甲虫的种群密度,
表示做窝的山地松甲虫的种群密度,
表示化学信号的浓度。当
且
时,王笑丹等人在文献 [10] 中证明了模型解全局存在且一致有界。当
且
,logistic源项为
时,Li和Tao证明了模型解全局存在且一致有界 [11] 。但是当
,此模型的解的性态不明确。本文,主要考虑一般的趋化敏感函数情况,假设趋化敏感函数
和函数
满足
(1.3)
(1.4)
(1.5)
与高维K-S模型解存在有限时间坍塌相比,模型(1.2)的解不会在有限时间内爆破。本文对于具有一般的趋化敏感函数的趋化模型(1.2)经典解的全局有界性结论如下:
定理1:假设非负初值
满足
、
和
,设
满足条件(1.3)~(1.5),则生物趋化模型(1.2)有唯一、非负经典解且关于时间一致有界。
2. 预备知识
为了证明定理1,先给出一些相关的引理。
引理2.1:假设非负初值
满足
、
和
。则存在
和非负函数
满足
使得
是模型(1.2)在
上唯一的经典解。而且
,则
证明:模型(1.2)经典解的局部存在性可利用不动点定理得到,详见文献 [12] [13] [14] 。
引理2.2:假设条件(1.3)~(1.5)成立,则存在常数
,使得模型(1.2)的解
满足
(2.1)
(2.3)
证明:对于模型(1.2)的第一个方程两边在
上积分,容易得出(2.1)式。对于模型(2.2)的第三个方程两边在
上积分,可得
那么,存在常数
,解得
接下来,引进一个有用的不等式,详见证明过程参考文献 [3] [14] 。
引理2.3:假设
则对所有的
满足
,
和
,则存在常数
使得
其中
且
3. 解的全局有界性
为了证明定理1,需要先建立
与
的有界性,下面给出一些相关的引理及其证明。
引理3.1:假设条件(1.3)~(1.5)成立,则存在常数
,
,使得对所有的
有
(3.1)
(3.2)
证明:首先定义函数
设
,
且
(3.3)
和
(3.4)
以及
(3.5)
通过直接计算,容易得到
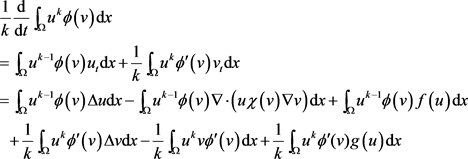
因为
,
和
以及
。那么可以得出
(3.6)
其中
此外,利用杨不等式估计和(1.3)式得出
和
那么,(3.6)式可以写成
(3.7)
根据题意,接下来处理(3.7)式中不等式右端的前两项,我们计算
和
那么有
根据(3.3)式,可知上式显然成立。
定义函数
。
所以
。
根据(3.5)式,有
则(3.7)式可改写为
那么根据引理2.3不等式和
得
其中
和
根据引理2.2的性质可得

因为
,可知
那么可以得出
容易解得这个常微分方程
下面证明(3.2)式,模型(1.2)中第三个方程同乘
再在
上积分得
利用杨不等式可得
那么存在常数
,使得下式成立
容易得出
4. 定理1的证明
由引理2.1可知,对于
,存在
可得
根据热半群理论 [14] ,设
,
使得
,容易得出
由算子理论和引理3.1,可以得到
其中c为一个正的常数,那么存在常数 ,由嵌入定理可得
,由嵌入定理可得
对于任意的
,通过模型(1.2)的第一个方程计算,容易得到
其中
,那么有
其中
那么,可以得到
解得
定义函数
设
,那么可知
令
,可以得到
对于
,根据
,解得
即
那么可以得到
5. 结论
综上所述,证明了高维空间中具有间接信号产出生物趋化模型解的全局有界性,但模型(1.2)有数值模拟等问题仍可继续研究。
基金项目
伊犁师范学院研究生科研创新项目《一类生物趋化模型解的存在性和渐近性》 (YLSF2017031);自治区青年科技创新人才培养项目“偏微分方程理论及其在图像处理中的应用” (2017Q081)。
NOTES
*通讯作者。