1. 引言
令
为一个有界光滑区域,所谓
上可测函数f生成的重排函数空间
是指由所有满足条件:
的可测函数g组成的全体。
如果可行集为某个可测函数的所有重排函数组成的重排函数空间,则在此可行集上考虑的最优化问题即是重排优化问题。重排优化问题的相关理论最早由Burton建立,见参考文献 [1] [2] 。之后许多作者在寻找重排优化问题最优解的存在性和唯一性以及对称性等不同方面做了很多更为广泛的研究,见参考文献 [3] - [9] 。
值得注意的是,以上文献中研究的都是Laplace算子等局部算子相关的重排优化问题。非局部算子相关的重排优化问题研究结果并不多见。
在文献 [10] 中,我们考虑了如下边值问题
(1.1)
相关的重排优化问题,其中
是如下定义的分数阶Laplace型非局部算子
,
更多非局部算子相关的重排优化问题研究结果见 [11] [12] 。
在文献 [10] 中,扰动项
关于第二变元单调非增是方程(1.1)存在唯一解的一个重要假设条件。
本文将考虑如下的扰动方程
引出的重排优化问题,其中
为一个参数,
为某个可测函数。
容易看出,扰动项
关于第二变元是单调递增的,这是与文献 [10] 中关于扰动项
条件的一个重要区别。
记
为方程
的能量泛函,即
(1.2)
假设
为可测函数,本文将研究下述重排优化问题:是否存在
使得
(Opt)
?
其中
为方程
的唯一基态解(参见定理3.1)。
不同于文献 [11] [12] ,文献 [11] 考虑的是与非局部算子相关的第一特征值优化问题,文献 [12] 研究的为含分数阶Laplace算子的形状优化问题。与文献 [10] 不同,由于本文研究的重排优化问题(Opt)中具有两个独立选取的函数
和
,这将给我们的研究带来更多困难。
2. 预备知识
仍记
为一个有界光滑区域。定义分数阶Sobolev空间如下
,
其中
。
为Hilbert空间,其中u和v之间的内积定义为:
.
设
,则u的范数为
.
定义2.1 称
为方程
的一个解,如果
.
容易验证,方程
的能量泛函
且
.
所以,
为方程
的解当且仅当
。
在本文中,我们将记
为通常的空间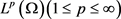 中的范数。记号C表示某个正常数。
中的范数。记号C表示某个正常数。
现在我们给出一些本文中常用的引理。
引理2.1 (见文献 [13] 引理8) 可以连续嵌入
可以连续嵌入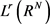 ,其中
,其中 且当
且当 时
时
是紧嵌入。
引理2.2 (见文献 [2] 引理2.1) 若 ,则对任意的
,则对任意的 都有
都有 且
且 。
。
引理2.3 (见文献 [7] 引理2.3) 设 ,
,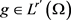 则存在
则存在 为关于
为关于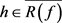 的线性泛函
的线性泛函 最大值点。
最大值点。
引理2.4 (见文献 [14] 引理6.2和定理6.1) 特征值方程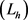
 (2.1)
(2.1)
的第一特征值 可表示如下:
可表示如下:
 (2.2)
(2.2)
且若 ,则存在
,则存在 使得
使得
 . (2.3)
. (2.3)
3. 方程 解的存在唯一性
解的存在唯一性
定理3.1 设 ,
,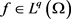 ,
, ,
,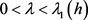 ,其中
,其中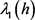 表示特征值方程
表示特征值方程
 的第一特征值,则方程
的第一特征值,则方程 存在唯一解
存在唯一解 ,且
,且 。
。
证明:第一步:证明方程 解的存在性。任取
解的存在性。任取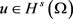 ,结合Holder不等式和引理2.1可得
,结合Holder不等式和引理2.1可得
 ,
,
其中 。
。
利用(1.2)和(2.2),容易知道
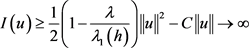 , 若
, 若 ,
,
所以泛函I是强制的。
容易看出泛函I是弱下半连续的。因此,I存在一个全局极小点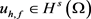 即
即 。又
。又 ,则由全局极小原理可得
,则由全局极小原理可得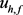 是方程
是方程 的一个解,即
的一个解,即
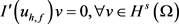 .
.
第二步:证明方程 解的唯一性。
解的唯一性。
利用反证法,假设存在 是方程
是方程 的解且
的解且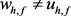 ,即至少存在一个正测集
,即至少存在一个正测集 使得
使得
 . (2.4)
. (2.4)
由定义2.1可知,对任一个 都有
都有
 ,
,
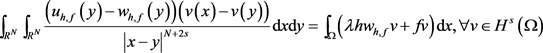 .
.
上两式相减可得
 .
.
特别地,令 并注意到
并注意到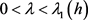 ,
, 则由(2.2),(2.4)可知
则由(2.2),(2.4)可知

矛盾。
综上:方程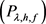 存在唯一解
存在唯一解 。
。
注:若 ,
, 是方程
是方程 的一个解,令
的一个解,令 是方程
是方程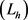 的特征函数,则容易验证,对任意的
的特征函数,则容易验证,对任意的 和
和 都有
都有
 .
.
由定义2.1,这表明 也是方程
也是方程 的解。因此,本文只考虑
的解。因此,本文只考虑 的情形以保证方程
的情形以保证方程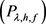 解的唯一性。
解的唯一性。
4. 重排优化问题(Opt)的可解性
定理4.1 设 ,
, ,
,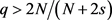 ,
, ,其中
,其中 由(2.3)定义,则问题(Opt)是可解的,即存在
由(2.3)定义,则问题(Opt)是可解的,即存在 ,
, 使得
使得
 ,
,
其中 表示方程
表示方程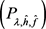 的唯一解。
的唯一解。
证明:令 ,其中
,其中 为对应方程
为对应方程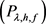 的唯一解,则A是有意义的,即
的唯一解,则A是有意义的,即 。
。
事实上,任取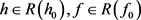 ,则由(2.2)和(2.3)容易验证
,则由(2.2)和(2.3)容易验证
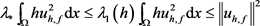 .
.
再利用Holder不等式和引理2.1可以知道,
 . (4.1)
. (4.1)
又由引理2.2,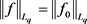 ,所以由上式可以得到A一定是有限数,即A是良定义的。
,所以由上式可以得到A一定是有限数,即A是良定义的。
任取 为一个极小化序列,即
为一个极小化序列,即 ,
, 且
且
 ,
,
其中 。由不等式(4.1)可知
。由不等式(4.1)可知 在
在 中有界,则存在子列(不妨仍记为
中有界,则存在子列(不妨仍记为 )弱收敛于
)弱收敛于 且强收敛于u在
且强收敛于u在 中。记
中。记 为
为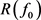 在
在 中的弱闭包。因为
中的弱闭包。因为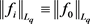 ,则
,则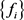 也存在子列(不妨仍记为
也存在子列(不妨仍记为 )弱收敛于某个
)弱收敛于某个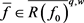 。因为
。因为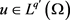 ,根据弱收敛的定义可得
,根据弱收敛的定义可得
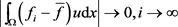 .
.
再利用Holder不等式,所以
 . (4.2)
. (4.2)
记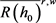 为
为 在
在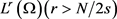 中的弱闭包。因为
中的弱闭包。因为 则
则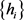 在
在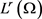 中有界,所以存在子列(不妨仍记为
中有界,所以存在子列(不妨仍记为 )弱收敛于某个
)弱收敛于某个 。通过类似地论证可以得到
。通过类似地论证可以得到
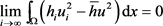 . (4.3)
. (4.3)
结合(4.2),(4.3)并利用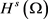 中范数的弱下半连续性,所以
中范数的弱下半连续性,所以
 (4.4)
(4.4)
由引理2.3,存在 为线性泛函
为线性泛函 的极大点。因此,
的极大点。因此,
 .
.
同理,存在 为线性泛函
为线性泛函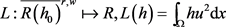 的极大点。因此,
的极大点。因此,
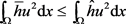 .
.
再结合(4.4),容易得到
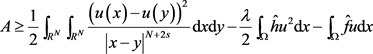 . (4.5)
. (4.5)
又由定理3.1,则
 . (4.6)
. (4.6)
由(4.5)和(4.6)即可推出, 。
。
注意到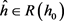 ,
, ,而由定义
,而由定义 ,所以显然
,所以显然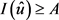 。
。
综上,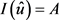 。命题得证。
。命题得证。
基金项目
本文得到国家自然科学基金项目(11771319)和江苏省自然科学基金青年基金(BK20150281,BK20170590)及江苏省高校自然科学研究面上项目(16KJB110020)的支持。