试位法的一种改进及其收敛性分析

An Improvement of the Regular Falsi Method and Its Convergence Analysis

摘要: 试位法是用数值方法求单变量非线性方程根的算法，方法简单易行。试位法作为二分法的改进，在大多数情况下优于二分法。本文结合二分法与试位法，给出了试位法的一种改进算法，并对其收敛情况进行了讨论，证明该算法的收敛性，给出了收敛指数的估计。

Abstract: The Regular Falsi method is an algorithm for finding the root of a univariate nonlinear equation by numerical method. The method is simple and easy. The Regular Falsi method is an improvement of the Bisection method and is superior to the Bisection method in most cases. In this paper, an improved algorithm of the test method is given by combining the dichotomy and the test position method. The convergence of the algorithm is proved and the convergence index is estimated.

1. 引言

通过数学分析的知识我们知道，对于单变量函数，给定一个区间，如果在这个区间上函数连续，且在两端点的值异号，则在这个区间内函数至少有一个零点，即方程 $f\left(x\right)=0$ 在这个区间内有实根。

假设函数 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上连续，在 $\left[a,b\right]$ 内有单根且在端点处的函数值异号，即 $f\left(a\right)f\left(b\right)<0$，

给出如下迭代格式：

$c=b-\frac{f\left(b\right)\left(b-a\right)}{f\left(b\right)-f(a)}$

如果 $f\left(c\right)f\left(b\right)<0$，则：令 $a=c$， $b=b$，继续进行上式的迭代过程；如果 $f\left(c\right)f\left(b\right)>0$，则按照如下改进后的迭代格式进行：

$c=b-\frac{f\left(b\right)\left(b-a\right)}{f\left(b\right)-\gamma f(a)}$

其中参数 $\gamma \in \left(0,1\right]$。改进后的格式被称为Illinois-type算法 [1] 。

2. 对参数的理解

2.1. 二分法

二分法是一种非常简单的数值方法，其基本原理是连续函数的介值定理。同上文假设的条件，计算区间 $\left[a,b\right]$ 中点处的函数值 $f\left(\frac{a+b}{2}\right)$。若则重置区间 $\left[a,b\right]$ 为 $\left[a,\frac{a+b}{2}\right]$ (反之取另一半区间 $\left[\frac{a+b}{2},b\right]$ 进行)，重复以上操作直至达到精度要求，根据区间套定理知如此构造的迭代序列收敛，且收敛速度与公比为 $\frac{1}{2}$ 的等比数列收敛速度相同 [2] 。

2.2. 试位法

设 $f\left(x\right)$ 在闭区间 $\left[a,b\right]$ 上连续且在端点处异号。以连接与 $B\left(b,f\left(b\right)\right)$ 的直线段L近似代替函数 $f\left(x\right)$ 的图像，而以L与x轴的交点坐标c作为 $f\left(x\right)$ 零点的近似。

根据三角形相似，可以建立求解c的方程：

$\frac{0-f\left(b\right)}{c-b}=\frac{f\left(b\right)-f\left(a\right)}{b-a}$

整理后即得：

$c=b-\frac{f\left(b\right)\left(b-a\right)}{f\left(b\right)-f(a)}$

若 $f\left(c\right)\ne 0$，则方程的实际根落在 $\left[a,c\right]$ 或 $\left[c,b\right]$ 中，选择这个区间重置原区间。重复如上过程直至 $\left|f\left(c\right)\right|$ 前后两次迭代结果的差小于事先设定的误差。

3. 收敛性分析

3.1. 收敛性

设 $f\left(x\right)\in C\left[a,b\right]$，对于迭代产生的序列 $\left[a_n,b_n\right]$，根据试位法的迭代原则知序列 $\left\{a_n\right\}$ 单调不减，序列 $\left\{b_n\right\}$ 单调不增，因此收敛，分别设其极限为 $d_1$， $d_2$，且有 $d_1\le d_2$。

1) 假设 $d_1$， $d_2$ 都不是 $f\left(x\right)$ 的根。

存在 $\epsilon >0$，正整数N，当时， $\left|f\left(a_n\right)\right|\ge \epsilon$， $\left|f\left(b_n\right)\right|\ge \epsilon$。由迭代格式知：

$c_n-a_n=\frac{f\left(a_n\right)\left(a_n-b_n\right)}{f\left(b_n\right)-f\left(a_n\right)}$， $c_n-b_n=\frac{f\left(b_n\right)\left(a_n-b_n\right)}{f\left(b_n\right)-f(an)}$

$\left|f\left(x\right)\right|$ 在 $\left[a,b\right]$ 上有界，设为M。则对于任意的正整数n，都成立

$\left|a_{n+1}-b_{n+1}\right|\le \max \left(\left|c_n-a_n\right|,\left|c_n-b_n\right|\right)\le \frac{M\left|a_n-b_n\right|}{M+\epsilon }$

因此，

$\left|a_{N+k}-b_{N+k}\right|\le {\left(\frac{M}{M+\epsilon }\right)}^k\left|a_N-b_N\right|$

从而得到

$\underset{n\to +\infty }{\lim }{a}_n=\underset{n\to +\infty }{\lim }{b}_n=d_1$

但是，既然对于任意的n，有 $f\left(a_n\right)f\left(b_n\right)<0$，这说明 $f\left(d_1\right)\ne 0$，即 $d_1$， $d_2$ 均不是方程 $f\left(x\right)=0$ 的根。

2) 假设 $d_1$ 是方程的根， $d_2$ 不是方程的根。

根据上述公式有

$\left|c_n-a_n\right|\le \frac{\left|f\left(a_n\right)\right|\left|a_n-b_n\right|}{\left|f\left(b_n\right)\right|}$

而不等式右端极限存在，为0，所以有

$\underset{n\to +\infty }{\lim }{c}_n=d_1$

同理，如果 $d_2$ 是方程的根， $d_1$ 不是方程的根，有 $\underset{n\to +\infty }{\lim }{c}_n=d_2$

3) 假设 $d_1$， $d_2$ 都是方程的根。若 $d_1\ne d_2$，则存在一子列 $c_i$ 收敛到 $d_1$，或有另一子列收敛到 $d_2$，即 $\underset{n\to +\infty }{\lim }{c}_n=d_1$。

下面我们证明，除非 $a_0$ 或者 $b_0$ 是 $f\left(x\right)$ 的根，或者对于某些n， $c_n$ 是 $f\left(x\right)$ 的根，就有 $d_1=d_2$。

假设 $d_1\ne d_2$，对于任意 $\delta >0$，存在正整数N，当 $n\ge N$ 时有：

$d_1-a_n<\delta$，

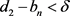
显然有，对于任意正整数n， $c_n<d_1$ 或 $c_n>d_2$。若对某些n成立 $c_n<d_1$，则：

$\frac{f\left(b_n\right)a_n-b_{n}f\left(a_n\right)}{f\left(b_n\right)-f\left(a_n\right)}<d_1$

且 $f\left(b_n\right)\le \frac{b_n-d_1}{d_1-a_n}$。不妨设 $f\left(a_n\right)<0$， $f\left(b_n\right)>0$。为了序列 $\left\{b_n\right\}$ 收敛到 $d_2$ ( $b_n>d_2$ )，必须有对于比n大的m，满足 $c_m>d_2$，这表明：

同理，对于大于n的p，有

$\left[-f\left(a_p\right)\right]\ge \frac{d_2-a_m}{b_m-d_2}f\left(b_m\right)\ge {\left(\frac{d_2-d_1}{\delta }\right)}^2\left[-f\left(a_n\right)\right]$

如此进行下去，则对于任给的 $F>0$，对于 $\left|f\left(x\right)\right|>F$，x趋近于 $d_2$。既然 $d_1$ 不是 $f\left(x\right)$ 的根，则 $\underset{n\to +\infty }{\lim }f\left(a_n\right)=0$，即。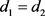

综上所述，迭代格式收敛。

3.2. 收敛速度

由上一部分证明知序列 $\left\{c_n\right\}$ 收敛。对于充分光滑的函数 $f\left(x\right)$，能求得序列 $\left\{c_n\right\}$ 收敛速度的下界 [2] 。设 $f\left(x\right)$ 连续二次可微，且在内有 $\left|f^{\prime }\left(x\right)\right|$ 不恒等于0；设 $x^{*}$ 是 $f\left(x\right)$ 的零点。根据试位法的迭代格式

$c_{n+1}-x^{*}=\frac{\left(b_n-x^{*}\right)f\left(a_n\right)-f\left(b_n\right)\left(a_n-x^{*}\right)}{f\left(a_n\right)-f(bn)}$

因为

$\frac{\text{d}}{\text{d}x}\left[\frac{f\left(x\right)}{x-x^{*}}\right]=\frac{f^{\prime }\left(x\right)\left(x-x^{*}-f\left(x\right)\right)}{{\left(x-x^{*}\right)}^2}$

根据Cauchy中值定理，存在 $\xi \in \left[a_n,b_n\right]$ 使得

$\frac{c_{n+1}-x^{*}}{\left(b_{n+1}-x^{*}\right)\left(a_{n+1}-x^{*}\right)}=\frac{f^{\prime }\left(\xi \right)\left(\xi -x^{*}\right)-f^{\prime }\left(\xi \right)}{f^{\prime }\left(\xi \right){\left(x-x^{*}\right)}^2}$

根据Taylor公式，有

$0=f\left(x^{*}\right)=f\left(\xi \right)+f^{\prime }\left(\xi \right)\left(x^{*}-\xi \right)+\frac{f^{″}\left(\theta \right)}{{\left(x^{*}-\xi \right)}^2}$

其中 $\theta$ 介于 $\xi$ 与 $x^{*}$ 之间。结合前一个式子，则有

$c_{n+1}-x^{*}=\frac{f^{″}\left(\theta \right)}{2f\left(\xi \right)}\left(b_n-x^{*}\right)\left(a_n-x^{*}\right)$

记 ${\epsilon }_n=c_n-x^{*}$， ${{\eta }^{}}_n=b_n-x^{*}$ ， ${{\eta }^{\prime }}_n=a_n-x^{*}$，则上式可写为

${\epsilon }_{n+1}=\frac{f^{″}\left(\theta \right)}{2f\left(\xi \right)}{\eta }_n{{\eta }^{\prime }}_n$

根据可微性的假设，存在正数m，M，使得对任意 $x\in \left[a,b\right]$，有 $\left|f^{\prime }\left(x\right)\right|\ge m$， $\left|f^{″}\left(x\right)\right|\le M$，则

$\left|{\epsilon }_{n+1}\right|\le \frac{M}{2m}\left|{\eta }_n\right|\left|{{\eta }^{\prime }}_n\right|$

用 $K=\frac{M}{2m}$ 乘不等式的两边，有

$K\left|{\epsilon }_{n+1}\right|\le K^2\left|{\eta }_n\right|\left|{{\eta }^{\prime }}_n\right|$

它等价于不等式 $d_{n+1}\le d_i{d}_j$，其中 $d_l=K\left|{\epsilon }_l\right|$ (注：这里将 $\eta$ 也用 $\epsilon$ 表示)。设初始逼近 $a_0$，满足

$d=\max \left\{d_0,{d^{\prime }}_0\right\}\le 1$

则迭代到第k步时， $d_{k+1}\le d^{k+1}$，这说明试位法是线性收敛的 [3] 。当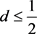时，试位法收敛速度快于二分法。

4. Illinois算法

4.1. 收敛性

Illinois算法很好地避免了不动点的出现，近似根从两端收敛到精确根，即迭代生成的新区间的长度

。基于这一条件，根据区间套定理以及一致连续定理，我们给出一下证明。

因为函数 $f\left(x\right)$ 在 $\left[a,b\right]$ 上连续，则 $f\left(x\right)$ 在 $\left[a,b\right]$ 上一致连续，即： $\forall \epsilon >0$， $\exists \delta >0$，只要 $\left|x_1-x_2\right|<\delta$，就有 $\left|f\left(x_1\right)-f\left(x_2\right)\right|<\epsilon$。则 $\forall \epsilon >0$， $\exists \delta >0$ ，当 $\left|b_n-a_n\right|<\delta$，就有 $\left|f\left(b_n\right)-f\left(a_n\right)\right|<\epsilon$。

对于上述 $\delta$， $\exists N$，当 $n>N$ 时，

$\left|b_n-a_n\right|=\left|b_n-x^{*}\right|+\left|x^{*}-a_n\right|<\delta$

则 $\left|f\left(b_n\right)-f\left(a_n\right)\right|<\epsilon$，即

$\left|f\left(b_n\right)-0\right|+\left|0-f\left(a_n\right)\right|<\epsilon$

因为 $\forall n$， $x^{*}\in \left[a_n,b_n\right]$，又因为 $\underset{n\to +\infty }{\lim }\left|b_n-a_n\right|=0$，根据区间套定理

$\underset{n\to +\infty }{\lim }{b}_n=x^{*}=\underset{n\to +\infty }{\lim }{a}_n$

则 $\underset{n\to +\infty }{\lim }f\left(b_n\right)=f\left(x^{*}\right)=\underset{n\to +\infty }{\lim }f(an)$

又因为 $a_n\le c_n\le b_n$，所以

$\underset{n\to +\infty }{\lim }{c}_n=x^{*}$

$\underset{n\to +\infty }{\lim }f\left(c_n\right)=f\left(x^{*}\right)=0$

即迭代序列收敛到方程的根。

4.2. 收敛速度

仍采用上文记号 ${\epsilon }_i$，令

$\beta =\frac{C_2}{C_1}$

$L={\beta }^2-\frac{C_3}{C_1}$

由上一小节证明，

${\epsilon }_{i+1}\sim L{\epsilon }_i{\epsilon }_{i-1}$

Illinois算法一次迭代包括先进行一次试位法，在进行两次修正 [4] ，则

${\epsilon }_{i+3}\sim L^2{\left({\epsilon }_i\right)}^3$

得到Illinois算法的收敛指数 [5] 为 $3^{\frac{1}{3}}$。即经过一次Illinois后，误差缩小为上一次的 $3^{\frac{1}{3}}$ 次方。

5. 函数实例

5.1. 不动点的情况

先来看一个出现不动点的情况： $f\left(x\right)=x^3+x^2-10$，初始区间为 $\left[-1,2\right]$。

在使用试位法求根时，出现了不动点 $x=2$ 的情况，迭代序列从左端点收敛到 $x^{*}=1.3652300$；而Illinois算法从第4次迭代开始不动点消失，迭代序列从两端收 $x^{*}$ ，收敛速度快于试位法；另外，当迭代相同次数时(10次)，后者精度高于前者。

5.2. 算例对比测试

选取了两个比较有代表性的算例进行了测试，将精度设定为10⁻¹⁵，计算结果如表1 (I代表Illinois算法，F代表试位法)。

Table 1. Comparison of examples between regular falsi method and illinois method

表1. 试位法与Illinois算法的算例对比

6. 总结

当函数接近线性时(图像上来看越接近直线)，该算法的效果明显。大多数情况下，试位法的效果会明

显优于二分法。但是，如果区间 $\left[a,b\right]$ 的长度比较大，曲线 $f\left(x\right)$ 在 $\left[a,b\right]$ 内某一点附近一阶导数值突然急

剧增长，在这种情况下，试位法出现了一个端点总是不动的情形，因此近似根只从一端收敛到精确根，这样它减慢了收敛速度，效果反而不如二分法。尤其当初始区间很大或函数在区间内偏离线性近似很远时收敛更慢。为了消除这种情况下的负面影响，可以对试位法做相应改进，在改进的试位法中，如果一个端点重复两次或更多次作为新的含根区间的端点(称为不动点)，则我们将这个点的函数值乘一个因子，使得线性插值的根更接近于精确根。这种改进真正体现了“试位”的思想。