1. 引言
分数阶微分方程的数值方法的精度常依赖于精确解的光滑性。针对精确解不光滑的情况,许多学者开始研究数值方法的修正格式,以保持离散格式的高精度。例如,Lubich [1] [2] [3] 给出基于1阶和2阶向后差分格式的两种修正方法,并给出收敛性分析。Yan [4] [5] 考虑L1格式的修正格式,并提出基于分段2次插值
的新型离散格式,然后给出其修正格式。Tadjeran [6] 提出分数阶扩散方程的2阶C-N格式,Jin [7] 接着考虑分数阶C-N格式的修正。在本文中,我们考虑齐次分数阶扩散方程的加权C-N格式,并针对精确解不光滑的情况提出比较简单的修正方法,只需修正原格式的第1步,即可保持格式的2阶时间精度。本文接着给出修正格式的收敛性分析,最后通过数值算例验证方法的有效性。
本文考虑如下齐次分数阶扩散方程:
(1)
其中
,
是Caputo时间分数阶导数,其定义为:
(2)
算子A表示有界正则区域上的自伴正定二阶椭圆偏微分算子 [4],满足
(3)
其中
表示
范数,记
为Riemman-Liouville导数,则有
。
2. 加权C-N格式及其修正格式
令
,则方程(1)可表示为:
(4)
令
为时间步长,
,h为空间步长,
。
表示
的向后Euler卷积逼近,其生成函数为:
(5)
分数阶导数的逼近格式在
时刻的时间精度为1阶,在
时刻的时间精度为2阶,对
在
时刻和
时刻作线性拉格朗日插值,可得
时刻的逼近格式
。带入方程(4),可得加权C-N格式:
(6)
在精确解不光滑的情况下,加权C-N格式达不到2阶时间精度。我们对加权C-N格式(6)的第1步得初值条件添加一个权系数
,适当选取 可使离散格式保持2阶精度,加权C-N修正格式如下:
可使离散格式保持2阶精度,加权C-N修正格式如下:
(7)
3. 加权C-N修正格式的收敛性分析
为了证明加权C-N修正格式的收敛性分析,我们先给出3个引理。
引理1:定义式子:
(8)
本文统一令
,
[1],当权系数
时,则有:
(9)
其中C为正常数。
证明:令
,
,则
,
,
,所以
,即可证得
。
引理2:定义式子:
(10)
(11)
则下式成立:
(12)
(13)
其中
表示
范数,C为正常数。
证明:令
,则
时,
,所以
,即
。
由引理1可得
,将
带入式(3)可得:
(14)
(15)
且下式成立:
(16)
带入式(10)即可证得式(12)和(13):
(17)
(18)
引理3:
分别由引理1和引理2定义,则下式成立:
(19)
证明:令
,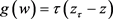 ,则
,
,
,所以可得
,即:
,则
,
,
,所以可得
,即:
(20)
由
( [8] 引理B.1),且由式(16)及可得:
(21)
其中
,即证得引理3。
为了给出收敛性分析,接下来我们分别借助Laplace变换和Cauchy积分公式,给出齐次分数阶扩散方程(4)的精确解和加权C-N修正格式(7)的数值解。对方程(4)作Laplace变换可得:
(22)
对式(21)作Laplace逆变换可得方程(4)的精确解:
(23)
其中
,
[4]。
考虑加权C-N修正格式(7),式子两边同乘
,并关于n求和,
,令
,于是
,由式(5)可得:
(24)
(25)
令
,由Cauchy积分公式及式(8)、(10)和(11)可得加权C-N修正格式的数值解:
(26)
定理1
分别为
时刻方程(4)的精确解和加权C-N修正格式(7)的数值解,则下式成立:
(27)
证明:
,而
,由引理1和引理2可得:
(28)
接着考虑
,令
,c为正常数,则:
(29)
(30)
则可证得
,即权系数取
时,加权C-N修正格式为时间2阶精度。
4. 数值算例
数值算例1:考虑如下齐次分数阶扩散方程:
(31)
该方程的精确解为
,u在
时不光滑。不同时间步长的误差如表1所示,不同
下的误差与对应步长的对数关系如图1所示,其中空间步长取
,统一取离散误差为
误差
。

Table 1. L 2 error of weighted C-N scheme (6) and weighted C-N modified scheme (7)
表1. 加权C-N格式(6)和加权C-N修正格式(7)的
误差
表1给出不同
及不同时间步长取值下,两种方法所得的误差。方法(a)为加权C-N格式离散,方法(b)为加权C-N修正格式离散,由表1可以看出,两种格式误差均收敛,且修正后的误差更小,方法更精确。
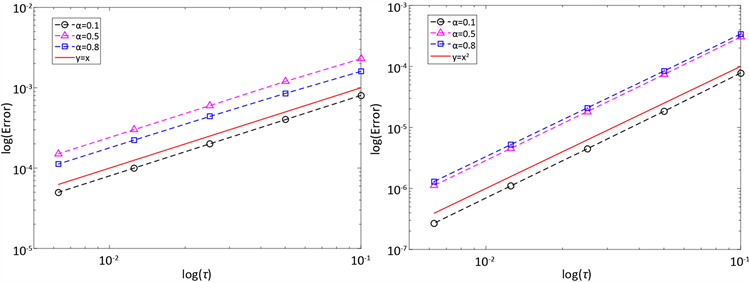
Figure 1. The relationship between error and time step
图1. 误差与时间步长的关系
图1给出不同
下误差与时间步长的关系,两坐标均为对数坐标,其中图1(a)为加权C-N格式,图1(b)为加权C-N修正格式。正如理论证明的结果一样,加权C-N格式只有1阶时间精度,而修正后的格式可达到2阶时间精度。
数值算例2:考虑如下齐次分数阶扩散方程:
(32)
该方程的精确解为
,u在
时不光滑。取
,不同时间步长下的两种格式的误差和精度如表2所示。

Table 2. Error and time accuracy of weighted C-N scheme (6) and weighted C-N modified scheme (7)
表2. 加权C-N格式(6)和加权C-N修正格式(7)的误差和时间精度
由表2可以看出,随着时间步长减小,两方法的误差均减小,但加权C-N格式只有1阶时间精度,而修正格式的精度可达到2阶。
基金项目
国家自然科学基金青年科学基金项目(61802129),广东省国家青年基金纵向协同项目(2018A030310381)。