具有广义Holling III型功能反应的Leslie捕食–食饵系统的平衡点分类和稳定性分析

Classification and Stability Analysis of Equilibrium Points in a Leslie Predator-Prey System with Generalized Holling Type III Functional Response

摘要: 在本文中，我们考虑一个具有Holling III型功能反应的Leslie型捕食–食饵系统。我们通过对原系统构造合适的变量变换，将其化为一个等价的系统。通过对等价系统的平衡点分类和稳定性进行分析，我们得出了原系统的平衡点分类和稳定性结果。

Abstract: In this paper, we consider a Leslie predator-prey system with Holling type III functional response. We construct a suitable variable transformation for the original system, and then obtain an equivalent system. By investigating the classification and stability of the equilibrium points of the equivalent system, we derive the results on the classification and stability of the equilibrium points of the original system.

1. 引言

考虑如下具有功能反应的Leslie捕食–食饵系统 [1] ：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{K}\right)-yp\left(x\right),\\ \frac{\text{d}y}{\text{d}t}=sy\left(1-\frac{y}{hx}\right).\end{array}$ (1)

其中， $x,y$ 分别表示食饵种群和捕食者种群的密度； $r,s>0$，分别表示食饵和捕食者的内在增长率； $K>0$，表示食饵的环境承载力； $h>0$， $\frac{1}{h}$ 是支撑一个捕食者所需的食饵数量。根据生态系统的意义，我们在区域 $G=\left\{\left(x,y\right)|x>0,y\ge 0\right\}$ 上讨论 [2]。

近几年来，Ali Atabaigi等研究了由Holling IV型或Monod-Haldane功能反应产生的Leslie型捕食者–食饵系统的平衡点的类型和稳定性 [3]。黄秀琴研究了一般形式的捕食–食饵模型的平衡点的类型和稳定性 [4]。本文受其启发，研究由广义Holling III型功能性反应 $p\left(x\right)=\frac{m{x}^2}{a{x}^2+bx+1}$ 产生的Leslie型捕食者–食饵系统：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{K}\right)-\frac{m{x}^{2}y}{a{x}^2+bx+1},\\ \frac{\text{d}y}{\text{d}t}=sy\left(1-\frac{y}{hx}\right).\end{array}$ (2)

$p\left(x\right)$ 是捕食者的摄取率作为食饵密度的函数 [5]。其中， $b>-2\sqrt{a},a>0,m>0$，对所有的 $x\ge 0$，使得 $a{x}^2+bx+1>0$，因此，对所有的 $x>0$， $p\left(x\right)>0$。

对系统(2)作变换：

$\bar{t}=rt,\bar{x}=\frac{x}{K},\bar{y}=\frac{mKy}{r},\bar{a}=a{K}^2,\bar{b}=bK,\delta =\frac{s}{r},\beta =\frac{s}{hm{K}^2}.$ (3)

将 $\bar{x},\bar{y},\bar{t},\bar{a},\bar{b}$ 仍记为 $x,y,t,a,b$，则系统(1)可以化为其等价系统：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\frac{x^{2}y}{a{x}^2+bx+1},\\ \frac{\text{d}y}{\text{d}t}=y\left(\delta -\frac{\beta y}{x}\right).\end{array}$ (4)

2. 系统的平衡点分析

对于任意的参数，系统(4)总是存在一个边界平衡点 $E_0=\left(1,0\right)$，并且 $E_0$ 是一个双曲鞍点。这个边界平衡点的生态学解释是：当缺乏捕食者时，食饵种群达到它的环境承载能力 [6]。平衡点 $E_0$ 将x轴正轴分成两个部分，这两个部分是 $E_0$ 的两个稳定流形，并且在G的内部，存在 $E_0$ 的唯一不稳定流形。

不失一般性，假设点 $E_1=\left(\bar{x},\bar{y}\right)$ 是系统(4)的任意正平衡点，则 $\bar{x}$ 是方程

$a{\bar{x}}^3+\left(\frac{\delta }{\beta }+b-a\right){\bar{x}}^2+\left(1-b\right)\bar{x}-1=0$ (5)

在区间 $\left(0,1\right)$ 上的根。由于系统(4)的正平衡点个数由方程(5)在区间 $\left(0,1\right)$ 上的根的个数决定，并且我们注意到，方程(5)在区间 $\left(0,1\right)$ 上可能有一个、两个或三个正根，则系统(4)在区间 $\left(0,1\right)$ 上可能有一个、两个或三个正平衡点。系统(4)在正平衡点 $E_1=\left(\bar{x},\bar{y}\right)$ 处的雅可比矩阵为

$J\left(E_1\right)=\left[\begin{array}{cc}1-2\bar{x}-\frac{\left(b{\bar{x}}^2+2\bar{x}\right)\bar{y}}{{\left(a{\bar{x}}^2+b\bar{x}+1\right)}^2}& \frac{-{\bar{x}}^2}{a{\bar{x}}^2+b\bar{x}+1}\\ \frac{\beta {\bar{y}}^2}{{\bar{x}}^2}& \delta -\frac{2\beta \bar{y}}{\bar{x}}\end{array}\right],$ (6)

并且雅可比矩阵的行列式和迹分别为

$Det\left(J\left(E_1\right)\right)=\left(\delta -\frac{2\beta \bar{y}}{\bar{x}}\right)\left(1-2\bar{x}-\frac{\delta \left(b{\bar{x}}^3+2{\bar{x}}^2\right)}{\beta {\left(a{\bar{x}}^2+b\bar{x}+1\right)}^2}\right)+\frac{\beta {\bar{y}}^2}{a{\bar{x}}^2+b\bar{x}+1},$ (7)

$Tr\left(J\left(E_1\right)\right)=1-2\bar{x}-\frac{\left(b{\bar{x}}^2+2x\right)\bar{y}}{{\left(a{\bar{x}}^2+b\bar{x}+1\right)}^2}+\delta -\frac{2\beta \bar{y}}{\bar{x}}.$ (8)

当 $Det\left(J\left(E_1\right)\right)=0$ 时， $E_1\left(\bar{x},\bar{y}\right)$ 是一个退化平衡点；当 $Det\left(J\left(E_1\right)\right)\ne 0$ 时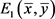，是一个基本的平衡点；当 $Det\left(J\left(E_1\right)\right)<0$ 时， $E_1\left(\bar{x},\bar{y}\right)$ 是一个双曲鞍点。

3. 主要结论及证明

类似于参考文献 [7]，考虑系统(4)的平衡点个数，我们能够得到下面的结论。

引理1：令 ${\Delta }_0={\left(\frac{\delta }{\beta }+b-a\right)}^2+3a\left(b-1\right)$， ${\Delta }_1=-4{\Delta }_0^3+{\left(27a^2+9a\left(1-b\right)\left(\frac{\delta }{\beta }+b-a\right)-2{\left(\frac{\delta }{\beta }+b-a\right)}^3\right)}^2$。

1) 如果 ${\Delta }_1>0$，则系统(4)有一个唯一的正平衡点 $E^{\ast }=\left(x^{\ast },y^{\ast }\right)$，它是一个基本的平衡点，并且是一个反鞍点；

2) 如果 ${\Delta }_1=0$，并且

2.1) ${\Delta }_0>0$，系统(4)有两个正平衡点：一个是基本的反鞍平衡点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{\beta \delta }{\beta \delta +{\left(1-\delta \right)}^2},\frac{{\delta }^2}{\beta \delta +{\left(1-\delta \right)}^2}\right)$，另一个是退化平衡点 $E^{\ast }\left(x^{\ast },y^{\ast }\right)=\left(1-\delta ,\frac{\delta }{\beta }\left(1-\delta \right)\right)$ ；

2.2) ${\Delta }_0=0$，则系统(4)有唯一的正平衡点 $E^{\ast }\left(x^{\ast },y^{\ast }\right)=\left(\frac{\text{3}}{1-b},\frac{\delta }{\beta }\frac{3}{1-b}\right)$，它是一个退化平衡点；

3) 如果 ${\Delta }_0<0$， $\frac{\delta }{\beta }\le a-b-\sqrt{3a\left(1-b\right)}$ 和 $-2\sqrt{a}<b<1$，则系统(4)有三个正平衡点 $E_1^{\ast }\left(x_1^{\ast },y_1^{\ast }\right)$， $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)$，和 $E_3^{\ast }\left(x_3^{\ast },y_3^{\ast }\right)$，它们都是基本的平衡点，并且 $E_3^{\ast }\left(x_3^{\ast },y_3^{\ast }\right)$ 是一个鞍点。

引理1的证明：对于引理中的情形1)，唯一的正平衡点的稳定性容易证明。本文只证明引理中的情形2.1)。

首先寻找一些参数，使得系统(4)有一个非双曲平衡点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)$，且 $Det\left(J\left(E_2^{\ast }\right)\right)>0,Tr\left(J\left(E_2^{\ast }\right)\right)=0$，和一个退化平衡点 $E^{\ast }\left(x^{\ast },y^{\ast }\right)$，且 $Det\left(J\left(E^{\ast }\right)\right)=0,Tr\left(J\left(E^{\ast }\right)\right)=0$。

我们能够验证，如果 $Det\left(J\left(E^{\ast }\right)\right)=0,Tr\left(J\left(E^{\ast }\right)\right)=0$，则

$x^{\ast }=1-\delta ,y^{\ast }=\frac{\delta }{\beta }\left(1-\delta \right),a=\frac{{\left(\delta -1\right)}^2+\beta \delta }{\beta \delta {\left(1-\delta \right)}^2},b=\frac{{\left(\delta -1\right)}^3-2\beta \delta }{\beta \delta \left(1-\delta \right)}.$ (9)

其中， $0<\delta <1$，如果 $a=\frac{{\left(\delta -1\right)}^2+\beta \delta }{\beta \delta {\left(1-\delta \right)}^2}$， $b=\frac{{\left(\delta -1\right)}^3-2\beta \delta }{\beta \delta \left(1-\delta \right)}$， $0<\delta <1$，则系统(4)可以简化为其等价系统。

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\frac{x^{2}y}{\frac{{\left(\delta -1\right)}^2+\beta \delta }{\beta \delta {\left(1-\delta \right)}^2}{x}^2+\frac{{\left(\delta -1\right)}^3-2\beta \delta }{\beta \delta \left(1-\delta \right)}x+1},\\ \frac{\text{d}y}{\text{d}t}=y\left(\delta -\frac{\beta y}{x}\right).\end{array}$ (10)

解得系统(10)有两个正平衡点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{\beta \delta }{\beta \delta +{\left(1-\delta \right)}^2},\frac{{\delta }^2}{\beta \delta +{\left(1-\delta \right)}^2}\right)$， $E^{\ast }\left(x^{\ast },y^{\ast }\right)=\left(1-\delta ,\frac{\delta }{\beta }\left(1-\delta \right)\right)$。

定理1：如果 $\left(a,b,\beta \right)=\left(\frac{1+{\delta }^2}{{\left(1-\delta \right)}^3},-\frac{{\delta }^2+\delta +2}{1-\delta },\frac{{\left(1-\delta \right)}^3}{{\delta }^2\left(1+\delta \right)}\right)$，且 $0<\delta <1$，则系统(4)有两个正平衡点：

a) $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{1-\delta }{1+{\delta }^2},\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2\left(1+{\delta }^2\right)}\right)$ 是一个多重数为1的不稳定多重焦点；

b)是一个余维为2的尖点。

定理1的证明：如果 $\left(a,b,\beta \right)=\left(\frac{1+{\delta }^2}{{\left(1-\delta \right)}^3},-\frac{{\delta }^2+\delta +2}{1-\delta },\frac{{\left(1-\delta \right)}^3}{{\delta }^2\left(1+\delta \right)}\right)$，且 $0<\delta <1$，则系统(4)化为等价系统。

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\frac{x^{2}y}{\frac{1+{\delta }^2}{{\left(1-\delta \right)}^3}{x}^2-\frac{{\delta }^2+\delta +2}{1-\delta }x+1},\\ \frac{\text{d}y}{\text{d}t}=y\left(\delta -\frac{{\left(1-\delta \right)}^3}{{\delta }^2\left(1+\delta \right)}\frac{y}{x}\right).\end{array}$ (11)

系统(10)有两个正平衡点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{1-\delta }{1+{\delta }^2},\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2\left(1+{\delta }^2\right)}\right)$ 和 $E^{\ast }\left(x^{\ast },y^{\ast }\right)=\left(1-\delta ,\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2}\right)$。

a) 令 $u=x-\frac{1-\delta }{1+{{\displaystyle \delta }}^2},v=y-\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2\left(1+{\delta }^2\right)}$，将点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)$ 转化为原点，系统(11)围绕原点的泰勒展开形式为

$\begin{array}{c}\frac{\text{d}u}{\text{d}t}=\delta u-\frac{{\left(1-\delta \right)}^3}{{\delta }^2\left(1+{\delta }^2\right)}v+\left(1+\delta +{\delta }^3\right)u^2+\frac{{\left(1-\delta \right)}^4}{{\delta }^3}uv+\frac{\left(1+\delta \right)\left(1+{\delta }^2\right)\left(1+\delta -{\delta }^2+3{\delta }^3-{\delta }^4+{\delta }^5\right)}{\left(-1+\delta \right){\delta }^2}{u}^3\\ +\frac{{\left(1-\delta \right)}^2\left(2-\delta +3{\delta }^2-{\delta }^3+{\delta }^4\right)}{{\delta }^3}{u}^{2}v+{\rm O}\left({\left|u,v\right|}^4\right)\end{array}$ (12)

$\begin{array}{c}\frac{\text{d}v}{\text{d}t}=\frac{{\delta }^4\left(1+\delta \right)}{{\left(1-\delta \right)}^3}u-\delta v-\frac{{\delta }^4\left(1+\delta \right)\left(1+{\delta }^2\right)}{{\left(1-\delta \right)}^4}{u}^2+\frac{2\delta \left(1+{\delta }^2\right)}{1-\delta }uv-\frac{{\left(1-\delta \right)}^2\left(1+{\delta }^2\right)}{{\delta }^2\left(1+\delta \right)}{v}^2+\frac{{\delta }^4\left(1+\delta \right){\left(1+{\delta }^2\right)}^2}{{\left(1-\delta \right)}^5}{u}^3\\ -\frac{2\delta {\left(1+{\delta }^2\right)}^2}{{\left(1-\delta \right)}^2}{u}^{2}v+\frac{\left(1-\delta \right){\left(1+{\delta }^2\right)}^2}{{\delta }^2\left(1+\delta \right)}u{v}^2+{\rm O}\left({\left|u,v\right|}^4\right)\end{array}$ (13)

对(12)和(13)作变换：

$u=\sqrt{\frac{{\left(1-\delta \right)}^7}{{\delta }^5{\left(1+{\delta }^2\right)}^2\left(1+{\delta }^2\right)}}x+\frac{{\left(1-\delta \right)}^3}{{\delta }^3\left(1+\delta \right)}y,v=y.$ (14)

则系统(12)和(13)可以化为其等价系统

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=-\sqrt{\frac{{\delta }^3\left(1-\delta \right)}{1+{\delta }^2}}y+f\left(x,y\right),\\ \frac{\text{d}y}{\text{d}t}=\sqrt{\frac{{\delta }^3\left(1-\delta \right)}{1+{\delta }^2}}x+g\left(x,y\right).\end{array}$ (15)

其中，

$\begin{array}{c}f\left(x,y\right)=\frac{\sqrt{{\left(1-\delta \right)}^7}\sqrt{{\delta }^5{\left(1+\delta \right)}^2\left(1+{\delta }^2\right)}\left(-1-\delta +{\delta }^2-2{\delta }^3+{\delta }^4\right)}{{\delta }^5\left(-1-\delta +{\delta }^4+{\delta }^5\right)}{x}^2+\frac{{\left(1-\delta \right)}^3\left(3+2\delta -{\delta }^2+2{\delta }^3\right)}{{\delta }^3\left(1+\delta \right)}xy\\ +\frac{\sqrt{{\delta }^5{\left(1+\delta \right)}^2\left(1+{\delta }^2\right)}{\left(1-\delta \right)}^6\left(2+\delta -{\delta }^2+{\delta }^3\right)}{\sqrt{{\left(1-\delta \right)}^7}{\delta }^6{\left(1+\delta \right)}^2}{y}^2+\frac{{\left(1-\delta \right)}^5\left(-1-\delta +2{\delta }^2-3{\delta }^3+{\delta }^5-{\delta }^6+{\delta }^7\right)}{{\delta }^7{\left(1+\delta \right)}^2}{x}^3\\ +\frac{\sqrt{{\delta }^5{\left(1+\delta \right)}^2\left(1+{\delta }^2\right)}\left(1-\delta \right)\left(-3-3\delta +8{\delta }^2-8{\delta }^3-{\delta }^4+6{\delta }^5-4{\delta }^6+3{\delta }^7\right)}{{\delta }^{10}{\left(1+\delta \right)}^3}\\ -\frac{{\left(1-\delta \right)}^5\left(3+3\delta -4{\delta }^2+14{\delta }^3-12{\delta }^4+14{\delta }^5-5{\delta }^6+3{\delta }^7\right)}{{\delta }^8\left(1+\delta \right)}x{y}^2\\ -\frac{\sqrt{{\left(1-\delta \right)}^7}\left(1-\delta \right){\left(1+{\delta }^2\right)}^2\left(1+\delta -3{\delta }^2+4{\delta }^3-2{\delta }^4+{\delta }^5\right)}{{\delta }^6\sqrt{{\delta }^5{\left(1+\delta \right)}^2\left(1+{\delta }^2\right)}}{y}^3+{\rm O}\left({\left|x,y\right|}^4\right)\end{array}$ (16)

$g\left(x,y\right)=-\frac{{\left(1-\delta \right)}^3}{\delta \left(1+\delta \right)}{x}^2+\frac{{\left(-1+\delta \right)}^2\sqrt{{\left(1-\delta \right)}^7}\sqrt{{\delta }^5{\left(1+\delta \right)}^2\left(1+{\delta }^2\right)}}{{\delta }^6{\left(1+\delta \right)}^3}{x}^3+\frac{{\left(1-\delta \right)}^5\left(1+{\delta }^2\right)}{{\delta }^4{\left(1+\delta \right)}^2}{x}^{2}y+{\rm O}\left({\left|x,y\right|}^4\right)$ (17)

Liapunov常数 [8] [9] 为

$\begin{array}{c}\mathrm{Re}{c}_1=\frac{1}{16}\{\left(f_{xxx}+f_{xyy}+g_{xxy}+g_{yyy}\right)\\ +\frac{1}{\omega }{\left[f_{xy}\left(f_{xx}+f_{yy}\right)-g_{xy}\left(g_{xx}+g_{yy}\right)-f_{xx}{g}_{xx}+f_{yy}{g}_{yy}\right]\}|}_{x=y=0}\\ =\frac{{\left(-1+\delta \right)}^2\left(-3+2\delta -8{\delta }^2+{\delta }^3-{\delta }^5+{\delta }^6\right)}{8{\delta }^8\left(1+\delta \right)}>0\end{array}$ (18)

其中， $\omega =\frac{{\delta }^3\left(1-\delta \right)}{14\pi \left(1+{\delta }^2\right)}$，由于 $0<\delta <1$，则 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{1-\delta }{1+{\delta }^2},\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2\left(1+{\delta }^2\right)}\right)$ 是一个多重数为1的不稳定多重焦点。

b) 作变换：

$x_1=x-\left(1-\delta \right)，x_2=y-\frac{{\delta }^3\left(1+\delta \right)}{{\left(1-\delta \right)}^2}.$ (19)

则系统(15)简化为其等价系统

$\{\begin{array}{l}\frac{\text{d}{x}_1}{\text{d}t}=\delta x_1+\frac{{\left(-1+\delta \right)}^3}{{\delta }^2\left(1+\delta \right)}{x}_2-\frac{2+\delta }{1+\delta }{x}_1^2+\frac{{\left(1-\delta \right)}^3}{{\delta }^3\left(1+\delta \right)}{x}_1{x}_2+{\rm O}\left({\left|x_1,x_2\right|}^3\right),\\ \frac{\text{d}{x}_2}{\text{d}t}=\frac{{\delta }^4\left(1+\delta \right)}{{\left(1-\delta \right)}^3}{x}_1-\delta x_2-\frac{{\delta }^4\left(1+\delta \right)}{{\left(1-\delta \right)}^4}{x}_1^2+\frac{2\delta }{1-\delta }{x}_1{x}_2-\frac{{\left(1-\delta \right)}^2}{{\delta }^2\left(1+\delta \right)}{x}_2^2+{\rm O}\left({\left|x_1,x_2\right|}^3\right).\end{array}$ (20)

作变换：

$y_1=x_1,y_2=\delta x_1+\frac{{\left(-1+\delta \right)}^3}{{\delta }^2\left(1+\delta \right)}{x}_2.$ (21)

则系统(20)可以化为等价系统

$\{\begin{array}{l}\frac{\text{d}{y}_1}{\text{d}t}=y_2-\frac{1}{1+\delta }{y}_1^2-\frac{1}{\delta }{y}_1{y}_2+{\rm O}\left({\left|y_1,y_2\right|}^3\right),\\ \frac{\text{d}{y}_2}{\text{d}t}=-\frac{\delta }{1+\delta }{y}_1^2-y_1{y}_2+\frac{1}{1-\delta }{y}_2^2+{\rm O}\left({\left|y_1,y_2\right|}^3\right).\end{array}$ (22)

在原点 $\left(0,0\right)$ 的一个小邻域内作变换：

$z_1=y_1-\frac{2\delta -1}{2\delta \left(1-\delta \right)}{y}_1^2,z_2=y_2-\frac{1}{1+\delta }{y}_1^2-\frac{1}{1-\delta }{y}_1{y}_2.$ (23)

则系统(22)可以化为等价系统

$\{\begin{array}{l}\frac{\text{d}{z}_1}{\text{d}t}=z_2+{\rm O}\left({\left|z_1,z_2\right|}^3\right),\\ \frac{\text{d}{z}_2}{\text{d}t}={\mu }_1{z}_1^2+{\mu }_2{z}_1{z}_2+{\rm O}\left({\left|z_1,z_2\right|}^3\right).\end{array}$ (24)

其中， ${\mu }_1=\frac{-\delta }{1+\delta },{\mu }_2=-\frac{\delta +3}{1+\delta }$，因为 ${\mu }_1{\mu }_2=\frac{\delta \left(\delta +\text{3}\right)}{{\left(1+\delta \right)}^2}\ne \text{0}$，所以平衡点 $E^{\ast }\left(x^{\ast },y^{\ast }\right)$ 是一个余维为2的尖点。定理得证，从而引理中的2.1)得证，即 ${\Delta }_0>0$ 时，系统(4)有两个不同的正平衡点：一个是基本的反鞍平衡点 $E_2^{\ast }\left(x_2^{\ast },y_2^{\ast }\right)=\left(\frac{\beta \delta }{\beta \delta +{\left(1-\delta \right)}^2},\frac{{\delta }^2}{\beta \delta +{\left(1-\delta \right)}^2}\right)$，另一个是退化平衡点 $E^{\ast }\left(x^{\ast },y^{\ast }\right)=\left(1-\delta ,\frac{\delta }{\beta }\left(1-\delta \right)\right)$。

致谢

感谢审稿老师及编辑老师提出的宝贵意见。