1. 引言
2012年,郭铁信教授与笔者建立了定义在完备随机度量空间上的Ekeland变分原理与Caristi不动点定理 [1]。经典泛函分析中,史树中教授在文献 [2] 中研究了完备度量空间上的Ekeland变分原理与Caristi不动点定理是等价的。这启发我们在随机度量理论中来思考这个问题。虽然目前还不能确定TC-拓扑下完备随机度量空间上Ekeland变分原理与Caristi不动点定理是否等价,但本文证明了在
-拓扑下两者确实是等价的。再者,利用两种拓扑下基本结果之间的关系,本文证明了在特殊的随机度量空间——随机赋范模上,Ekeland变分原理与Caristi不动点定理在两种拓扑下都是等价的;最后由完备随机赋范模上的Caristi不动点定理,在两种拓扑下建立了完备随机赋范模上的方向压缩不动点定理。
文献 [3] 与 [4] 也曾讨论过完备随机度量空间上的Ekeland变分原理与Caristi不动点定理及其等价性问题,但是本文与其有如下几点不同:首先相比较文献 [3] 与 [4] 中给出的随机度量空间上的下半连续函数的定义,本文中下半连续函数的定义更弱、更自然,而且我们允许函数取值于
,而文献 [3] 与 [4] 中仅仅允许函数取值于
,故我们的结果改进了 [3] 与 [4] 中的相应结果。再者,本文的结果是在两种拓扑
-拓扑与TC-拓扑下建立的,而文献 [3] 与 [4] 的结果仅是在
-拓扑下建立的。而且,相比较文献 [2] 的证明方法,本文的证明方法更为简洁。
2. 主要结果
在文献 [1] 中,郭铁信教授与笔者建立了
-完备RM-空间上的Ekeland变分原理的精确形式及一般形式,即如下引理1和引理2。
引理1 [1] (
-完备RM-空间上Ekeland变分原理的精确形式)
设
为以
为基的
-完备RM-空间,函数
为真的、
-下半连续的且有下界的函数。那么对于任意的
,存在
满足如下条件:
1)
;
2) 对于任意的
且
,有
成立,即存在
且
使得在
上
成立。
引理2 [1] (
-完备RM-空间上Ekeland变分原理的一般形式)
设
为以
为基的
-完备RM-空间,函数
为真的、
-下半连续的且有下界的函数。则存在
使得
。
其实,
-完备RM-空间上的Ekeland变分原理的这两种形式是等价的,证明如下。
定理1 引理1 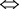 引理2。
引理2。
证明 显然由引理1 可得引理2;若将引理2中E的闭子集
来代替E,将
代替
,则得到引理1。故引理1等价于引理2。
下面的引理3为郭铁信教授与笔者建立的
-完备RM-空间上的Caristi不动点定理。
引理3 [1] (
-完备RM-空间上的Caristi不动点定理)
设
为以 为基的
-完备RM-空间,函数
为真的、
-下半连续的且有下界的函数。映射
满足
为基的
-完备RM-空间,函数
为真的、
-下半连续的且有下界的函数。映射
满足 则T有不动点。
则T有不动点。
下面我们证明
-完备RM-空间上的Ekeland变分原理与Caristi不动点定理即引理2与引理3是等价的。
定理2 引理2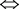 引理3。
引理3。
证明 1) 必要性:由引理2知,存在
,对于任意的
且
,有
成立,即存在
且
使得在
上
成立。我们可以推断
。否则,若
,则存在
且
使得在
上
成立。这与
产生矛盾。故
,即T有不动点。
2) 充分性:反证法。若引理2不成立,则对于任意的
,存在
使得
且
成立。定义函数
为
。则
且
成立。由
知,T无不动点。而由
成立及引理3知T有不动点。产生矛盾,故引理2成立。
由此,我们可知以上三个引理都是等价的,即
推论1 引理1
引理2
引理3。
郭铁信教授在长文 [5] 中系统地建立了上述提到的两种拓扑即
-拓扑及局部
-凸拓扑下导出的某些基本定理之间的内在关系,即两种拓扑下RN-模的完备性、闭集以及下半连续性之间的关系。又由于随机赋范模是特殊的随机度量空间,局部
-凸拓扑下完备随机赋范模上的Ekeland变分原理与Caristi不动点定理也是等价的。
由
-完备RM-空间上的Caristi不动点定理,可得如下
-完备RN-模上的方向压缩不动点定理。
推论2 (
-完备RN-模上的强压缩不动点定理)
设
为数域R上以
为基的
-完备RN-模。
且在
上
。
为
-连续函数且具有局部性质。若对于任意的
,存在
使得
且
1)
;
2)
。
则T有不动点。
证明 定义函数
如下:若
,则
;若
,则
。显然,函数T有不动点等价于f有不动点。
另定义函数
为
。因为T为
-连续函数,故
为
-连续函数。从而
为
-下半连续函数。
由T具有局部性质,故
从而
具有局部性质。显然,0是函数
的下界。
为了证明f有不动点,由引理3知,我们只需要证明
成立即可。
若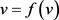 ,则显然
成立。
,则显然
成立。
若
,则
。由(1) (2)知,
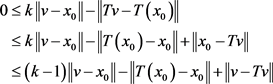
故
成立。
再由两种拓扑下随机赋范模的完备性以及下半连续函数的关系 [5],可得TC-完备的RN-模上的方向压缩不动点定理如下:
推论3 (TC-完备RN-模上的方向压缩不动点定理)
设
为数域R上以
为基的TC-完备RN-模且具有可数连结性质。
且在
上
。
为TC-连续函数且具有局部性质。若对于任意的
,存在
使得
且
1)
;
2)
。
则T有不动点。
3. 总结
本为在两种拓扑下证明了完备随机度量空间上的Ekeland变分原理与Caristi不动点定理的等价性。并在两种拓扑下建立了完备随机赋范模上的方向压缩不动点定理。
基金项目
国家自然科学基金(No: 11601030);北京市自然科学基金(No: 1194022);“十三五”时期北京市属高校高水平教师队伍建设支持计划(No: CIT&TCD201704071);北京联合大学人才强校优选-百杰计划(项目号:BPHR2018CZ09)。
NOTES
*通讯作者。