基于模式感知元分块技术的Web实体解析算法

Web Entity Resolution Algorithm Based on Schema-Aware Meta-Blocking Technology

摘要: 实体解析ER (Entity Resolution)是识别一个或多个数据源中同一实体记录。对于在多数据源中直接比较每对记录计算复杂度较大的问题，通常采用分块的方法。由于在Web数据源中大部分是模式未知的，通常采用元分块技术，虽然减少了丢失可能的匹配，但是增加了在同一块中放置不匹配实体记录的可能性。为此提出了一种基于局部敏感哈希的属性匹配归纳法从多个Web大数据集中对属性进行匹配划分，去除了属性间冗余的比较；然后通过一种基于聚合熵加权图的元分块技术，来提高Web数据源的分块质量，去除了分块中实体记录之间多余的比较，降低了算法的复杂度。最后采用实际数据集进行实验验证了该算法的有效性。

Abstract: Entity Resolution is the identification of the same Entity record in one or more data sources. For problems with high complexity of directly comparing each pair of records in multiple data sources, chunking is usually adopted. Since most of the Schema are unknown in Web data sources, Me-ta-blocking techniques are commonly used, which reduce the possibility of missing matches but in-crease the possibility of placing mismatched entity records in the same block. To solve the above problems, an attribute matching induction method based on locally sensitive hashing is proposed to conduct attribute’s matching division from multiple Web big data sets to remove redundant com-parison among attributes. Then, a block technique based on aggregation entropy weighted graph is used to improve the block quality of Web data sets, remove redundant comparisons in the blocks and reduce the complexity of the algorithm. Finally, the effectiveness of the algorithm is verified by experiments with actual data sets.

1. 引言

现阶段，实体解析问题是数据质量领域比较热门的研究领域。正如基于Web的实体和关系的挖掘来建立大型通用知识库那样，只有将不同的数据源集成时，这些数据的真正价值才会被挖掘出来以供企业、政府和研究人员利用 [1]。

实体解析指的是识别一个或多个数据源中同一实体记录的任务 [2]。对实体集合中所有可能匹配的记录进行比较是一个二次方问题。因此在庞大的数据集中采用传统的比较方法是不切实际的。为此，通常将类似的记录分块，然后只比较那些出现在同一块中的记录可以提高实体解析算法的效率。但是对于多个数据源中的数据来说，通常有着不同的模式，那么数据源之间的模式匹配就必须在实体解析之前进行。而对于Web上大量高度异构和有噪音的数据来说，传统的模式匹配将不再适用。目前主要采用模式未知(Schema-agnostic)的模块划分方法解决这个问题。传统的模式未知分块技术是标记分块(Token blocking) [3] [4]。这种技术指的是将数据集中出现的每个标记数据(Token)都看作是一个模块划分键 [2]。因此，每个分块会与一个标记数据相关联，并且包含这个标记数据出现的所有实体记录。标记分块可将每个记录都放置在多个分块中，虽然减少了丢失可能的匹配，但是却增加了不匹配的实体记录放置在同一个块中的可能性。本文在采用基于局部敏感哈希的属性匹配归纳的基础上引入并改进了一种松散模式感知的元分块技术 [5] [6]，在保证较高的召回率的同时，也提高了精准率。

本文主要贡献如下：

1) 将具有大量属性的Web源数据集中的属性依据信息熵和等价类的方法进行属性选择和分类，以减少数据集中的不相关属性的比较；

2) 引入了局部敏感哈希的预处理步骤，将属性匹配归纳法(Attribute-match induction)应用到具有大量属性的Web数据集中，利用属性匹配归纳法进行属性匹配和划分，以减少不相关的属性之间冗余比较；

3) 依据属性匹配和划分的模式信息，利用改进了的基于聚合熵加权图的元分块方法消除了多余比较；

4) 最后对该算法进行了实验验证。

2. 相关工作

在实体解析(ER)中为了提高效率通常采用分块技术 [7] [8]，现阶段的分块技术分为两大类：一类是基于模式的分块技术，有后缀数组(Suffix Array) [3]，q-grams [9]，和Canopy Clustering [10] 等方法，另一类是模式未知的分块技术，例如：标记分块(Token Blocking) [4] 和属性匹配归纳法(Attribute-match induction) [4] [11]。

在模式未知的分块技术中，属性聚类(Attribute Clusting) [4] 和文献 [6] 中的方法TYPiMatch将统计出来的数据信息提取到特定的分块键中。属性聚类依赖于对数据集中所有可能匹配的属性进行比较，而对于那些相似度较高的属性对来说，这是一个低效的过程，因为绝大多数的比较都是多余的。本文基于局部敏感哈希的预处理步骤旨在解决这个问题。TYPiMatch [4] 是在Web通用数据集中从属性集中识别出频繁出现的字段(数值，字符串)，并使用这些信息来选择分块键，但是它不能有效地扩展到大数据集中。

元分块 [5] [6] 旨在提高数据分块技术产生的块集合质量。现有的元分块技术是完全模式未知的。在本文中采用的是利用Web数据源中松散模式信息的元分块技术，来提高分块质量。

3. 相关概念及理论

3.1. 相关概念及评价方法

实体概要：

由一个特殊的标识符和一组属性名和属性值组成的元组 $\left\{\langle a_1,v_1\rangle ,\langle a_2,v_2\rangle ,\langle a_3,v_3\rangle ,\cdots ,\langle a_n,v_n\rangle \right\}$。在这里用 $A_{\epsilon }=\left\{a_1,a_2,a_3,\cdots ,a_4\right\}$ 表示与实体集合 $\epsilon =\left\{p_1,p_2,p_3,\cdots ,p_n\right\}$ 相关联的一组有匹配可能性的属性集。实体

集合 $\epsilon$ 是一组实体记录。如果两个实体记录 $p_i,p_j\in \epsilon$ 指向现实世界同一个对象那么它们是匹配的( $p_i\approx p_j$ )；实体解析(ER)是识别给定的实体集合 $\epsilon$ 中相匹配实体记录的任务。

实体解析主要分为两种情况：

1) Clean-Clean ER：输入两个无重复的实体集合 ${\epsilon }_1$ 和 ${\epsilon }_2$ ，并对来自不同数据源中的实体概要

$\left\{\left(p_i,p_j\right)|p_i\in {\epsilon }_1,p_j\in {\epsilon }_2\right\}$ 进行比较，对Clean-Clean ER最直接的解决方法需要 $\left|{\epsilon }_1\right|\times \left|{\epsilon }_2\right|$ 次比较；

2) dirty ER：输入含有重复记录的集合 $\epsilon$ ，并对所有可能匹配的实体概要进行了比较。最直接的解决方法是执行 ${\left|{\epsilon }_i\right|}^2$ 次比较。 $\left|{\epsilon }_i\right|$ 是一个实体集合 ${\epsilon }_i$ 的基数。

实现实体解析的有效途径是对实体概要进行适当的模块划分，即根据模块划分键(索引准则)索引相似的实体概要，将实际的比较限制在同一块中，以减少实体解析算法复杂性。使用 $\beta =\left\{b_1,b_2,\cdots ,b_i\right\}$ 表示一组块集合，它的基数 $\Vert \beta \Vert ={\displaystyle {\sum }_{b_i\in \beta }\Vert b_i\Vert }$ ，其中 $\Vert b_i\Vert$ 是块 $b_i$ 中的比较次数。

本文使用召回率(PC)和精准率(PQ)来评估块集合 $\beta$ 的质量 [7]。 $PC\left(\beta \right)$ 指检测到的重复实体概要与实际重复实体概要之间的比值； $PQ\left(\beta \right)$ 指的是实际的比较次数中有效的比较所占的比率。本文还引入了F₁-score [7]。

公式： $PC\left(\beta \right)=\frac{\left|D^{\beta }\right|}{\left|D^{\delta }\right|}$ ； $PQ\left(\beta \right)=\frac{\left|D^{\beta }\right|}{\Vert \beta \Vert }$ ； $F_1\left(\beta \right)=2\cdot \frac{PC\left(\beta \right)\cdot PQ\left(\beta \right)}{PC\left(\beta \right)+PQ(\beta )}$

$D^{\beta }$ 是在块 $\beta$ 中出现的一组重复实体概要， $D^{\delta }$ 是一组在集合 $\epsilon$ 中出现的所有重复实体概要。

通常情况下，模式未知的模块划分(元分块)可以保证较高的召回率(PC)，但牺牲了精准率(PQ)。低精确率(PQ)是由于多余的比较造成的：冗余的比较指重复的比较一组实体概要；多余的比较是对非匹配的实体概要进行的比较( $p_i\cancel{\approx }{p}_j$ )。

因此本文采用属性匹配归纳法和元分块方法来减少这些多余和冗余的比较，来提高实体解析算法的效率。

3.2. 属性匹配归纳法

属性匹配归纳法的目标是，在模式未知的情况下，在两个实体集合 ${\epsilon }_1,{\epsilon }_2$ 中从属性值的分布规律中归纳出相似度较高的属性对组。可以利用这些信息来提高模式不可知的分块技术的效率。

属性匹配归纳法：给定两个实体集合 ${\epsilon }_1,{\epsilon }_2$ ，依据相似度测量来识别相似属性对

$\left\{\langle a_i,a_j\rangle |a_i\in A_{{\epsilon }_1},a_j\in A_{{\epsilon }_2}\right\}$ ，并利用这些属性对来产生属性分区。即，将属性名称空间 $\left(A_{{\epsilon }_1}\times A_{{\epsilon }_2}\right)$ 划分成不重叠的子集。

属性对空间的聚类划分主要基于四个步骤：属性值转换、属性表示模型、属性对的相似性度量和聚类算法。

i) 属性值转换：给定两个实体集合 ${\epsilon }_1,{\epsilon }_2$ ，使用元组 $\langle a_j,\tau \left(V_{a_j}\right)\rangle$ 表示实体集合中的每一个属性， $a_j\in A_{{\epsilon }_i}$ 是一个属性名， $\tau$ 是一个属性值转换函数，生成一组从值 $V_{a_j}$ 中派生出来的标记来表示属性 $a_j$ 存在于

$\epsilon$ 中。函数 $\tau$ 通常是一组文本转换函数(包括标记化、去除禁用词、词元化等)。给定一个转换函数 $\tau$ ，

两个实体集合 ${\epsilon }_1$ 和 ${\epsilon }_2$ 中可能的属性值就是 $T_A=T_{a_{{\epsilon }_1}}\cap T_{a_{{\epsilon }_2}}$ ，其中 $T_{a_{\epsilon }}={\displaystyle {\cup }_{a_i\in A_{\epsilon }}\tau \left(V_{a_i}\right)}$。

ii) 属性表示模型：用矢量 $T_i$ 来表示每一个属性 $a_i$ ，每一个值 $v_{in}\in T_i$ 与元素 $t_i\in T_A$ 相关联。如果 $t_n\notin \tau \left(V_{a_i}\right)$ ，那么 $v_{in}$ 就等于0。如果 $t_n\in \tau \left(V_{a_i}\right)$ ，那么 $v_{in}$ 就使用加权函数计算的值表示，比如：加权函数可采用TF-IDF(t_n)，或者在 $\tau \left(V_{a_i}\right)$ 中的元素 $t_n$ 使用二进制表示(即：如果 $t_n\in \tau \left(V_{a_i}\right)$ 那么 $V_{in}=1$ ，否则 $V_{in}$ 为

0)。例如：属性值转换 是将值转换成标记，采用二进制表示这些标记，然后把属性集被表示为一个矩阵：列对应于属性；行对应于实体集合中出现的可能的标记；如果标记 $t_n$ 出现在属性 $a_i$ 中，每一个元素表示为 $V_{in}=1$ 否则表示为0。

iii) 相似度测量：对于每一个可能的属性对 $\left(a_j,a_k\right)\in \left(A_{{\epsilon }_1}\times A_{{\epsilon }_2}\right)$ 的相似度，是通过测量矢量 $T_i$ 和 $T_k$ 的相似性来比较的(比如：相似性函数可采用Dice，Jaccard，Cosine)。注意，相似性度量方法必须与属性模型表示兼容；例如，Jaccard的相似度不能与TF-IDF的权值同时使用。

iv) 聚类算法：该算法输入属性表示模型及其实体概要的相似度，对它们的属性名进行非重叠分区，它的输出是属性分区。

3.3. 元分块

元分块的主要思想是重组一个由冗余分块技术生成的块集合，观测两个实体概要共用的属性块越多，匹配的概率就越大，在重组的同时，将它们放在同一个块中。

元分块：给定一个块集合 $\beta$ ，重构标记分块，采用剪枝策略生成一个新的块集合 ，在保证(PC)召回率不变的情况下提高了PQ (精准率)。即： $PQ\left({\beta }^{\prime }\right)\gg PQ\left(\beta \right)$ 以及 $PC\left({\beta }^{\prime }\right)\approx PC\left(\beta \right)$。

元分块图：使用加权图 $G_{\beta }\left\{V_{\beta },E_{\beta },W_{\beta }\right\}$ 表示一个块集合 $\beta$。 $V_{\beta }$ 表示所有 $p_i\in \epsilon$ 的节点集。如果两个实体概要至少在同一个块中出现一次，那么两个实体概要之间存在一条边： $E_{\beta }=\left\{e_{ij}:\exists p_i,p_j\in \epsilon |\left|{\beta }_{ij}\right|>0\right\}$ 是一组边； ${\beta }_{ij}={\beta }_i\cap {\beta }_j$ ， ${\beta }_i$ 和 ${\beta }_j$ 分别是包含 $p_i$ 和 $p_j$ 的两个块。 $W_{\beta }$ 是与边相关的一组权值。权值表示匹配的可能性；这是采用边修剪策略的基准，用来保留匹配可能性更大的边。

剪枝方法：在元分块技术中可以采用两种修剪方法，一种是基于基数的，指的是先确定比较的数量以及执行的时间然后依据 权重保留Top-k的边，但是这种方法牺牲了召回率；另一种是基于权值的，通过权重阈值来保留最有可能匹配的边。两种修剪标准都可以应用在局部或全局上。在第一种情况下，Top-k边和权重阈值 $\theta$ 可以应用在以节点为中心的剪枝策略中。即对每个节点及其相邻的边进行剪枝操作；在第二种情况下，Top-k边是在所有的边中选择的，阈值 $\theta$ 对于所有边都是唯一的。

剪枝策略：利用这些特征，可以组成四种修剪策略。权边修剪(WEP)去除所有的权值小于 $\theta$ 的边。基数边修剪(CEP)按降序对所有边进行排序，并且只保留前k个边。权值节点修剪(WNP)，依次考虑每个节点 $n_i$ 和它的相邻边，并修剪那些低于全局阈值 ${\theta }_i$ 的边。类似于WNP的基数节点修剪(CNP)是以节点为中心的，但是不是一个权重阈值，而是采用了基数阈值 $k_i$ (即：为每个节点保留Top $k_i$ 个边)。

在修剪的最后，每一组由边连接的节点构成的连通图组成一个新的块。当两个相匹配的实体概要最终只能出现在同一个块集合中时，元分块就从根本上消除了冗余的比较。

4. 松散模式感知元分块方法模型

主体思想：首先采用一种属性匹配归纳法对多个Web数据集中属性进行匹配划分，然后重组基于标记分块方法的块集合，组成元分块图，最后利用聚合熵对基于图的元分块加以改进，以达到对多数据源进行实体解析的目的。

该方法输入两个实体集合(图1)。主要由三个阶段组成，如图2中：单数据源属性选择、多数据源松散属性匹配归纳、基于聚合熵加权图的元分块。下面详细介绍下面的三个步骤。

Figure 1. (a) Collection of entity records from four different data sources; (b) Divide the generated block set with the tag module

图1. (a) 来自四个不同数据源的实体记录的集合；(b) 用标记模块划分生成的块集合

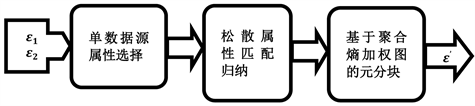
Figure 2. Flow chart of the loosely pattern-aware block method

图2. 松散模式感知元分块方法流程图

4.1. 单数据源属性选择

在单数据源中，由于数据集中含有大量的数据属性，这些数据属性对于接下来的实体解析来说，其重要程度是不同的，所以本文采用属性选择方法来选择相对重要的属性集，以减少所需分析数据属性比较的次数，使处理后的数据属性集能更有效的进行实体解析。

本文将属性分为两类：

分类属性：根据属性的取值，可以将其分为多个类别的属性。例如：楼盘类型可以分为别墅、洋房、高层等类别。

值属性：每一个属性值都是唯一存在的字符型以及数值型数据，不能将他们归为多个类的属性。例如：楼盘名、建筑面积等。

4.1.1. 分类属性选择

在信息论中，用熵(Entropy)表示随机变量不确定性的度量，也就是说熵值越大，其随机变量的不确定性就越大，即数据集中随机变量的取值就越多。设X是一个含有限个值的离散随机变量，p(x)为x在数据集X中的出现的概率，则随机变量X的熵定义为：

$H\left(X\right)=-\underset{i=1}{\overset{n}{{\displaystyle \sum }}}p\left(x\right)\log p(x)$

对于分类属性而言，属性熵值越大，划分后得到的子集纯度就越高，选择这类熵值较大的属性，去查找重复记录，更具备说服力。由于在单个数据源中分类属性的数量较多，所以在本文中，计算出每个分类属性的熵值 $H\left(X\right)$ 并且按照从大到小的顺序排列，然后选择熵值中间值作为阈值 $\epsilon$ ，熵值大于这个阈值 $\epsilon$ 的属性，将它们作为候选集以进行接下来的算法步骤。

4.1.2. 值属性选择

值属性包含了数值型属性和字符型属性，对于数值型属性选择之前需要对其进行离散化处理，本文采用等宽法将属性值分为具有相同宽度的区间，区间的个数K根据实际情况来决定，比如将建筑面积划

分为 $[70,90)$ 、 $[90,110)$ 、 $[110,130)$ 等。并使各个区间中的实体记录不存在交集。对于字符型属性，在进

行选择之前，采用上文3.2节中属性值转换的方法，将属性值进行规范化，例如：在不同数据源中表示相同的地址的方式是不一样的，采用属性值转换的方法，将此类属性值统一化。

对于值属性，在进行实体解析的时候其重要程度也是不一样的，如下表1中，建筑面积的信息量比楼盘名称的信息量要少。事实上有可能的是他们的楼盘是不同的但是建筑面积是相同的。在进行实体解析时，楼盘名称更能有效的判断是否重复，本文使用熵值为每个值属性分配一个权值，属性的熵值越大说明信息量越大，则该值属性更有说服力。同样的计算出每个值属性的信息熵 $H\left(X\right)$ ，然后选择熵值中间值作为阈值 $\epsilon$ ，熵值大于这个阈值 $\epsilon$ 的属性，将它们作为候选集以进行接下来的算法步骤。

Table 1. Part of the household table

表1. 部分户表

4.2. 多数据源松散属性匹配归纳法

这里介绍了一种属性匹配归纳法来对属性空间划分。此外，本文对属性聚类的主要改进是提出了一个基于局部敏感哈希的预处理步骤来扩展到Web大数据集中。

4.2.1. 局部敏感哈希预处理步骤

根据本文第3.2节中属性匹配归纳法的介绍，需要对所有可能匹配的属性对计算相似度，其中所需

的总的时间复杂度为 $O\left(N_1,N_2\right)$ ， $N_1,N_2$ 分别是 $A_{{\epsilon }_1}$ 和 $A_{{\epsilon }_2}$ 的基数。然而Web的半结构化数据通常涉及较

高的维度(数据源通常有成千上万个属性值)问题，采用传统的属性匹配归纳法划分属性组会导致较高的时间复杂度；并且，对于每个属性来说，只有少数或者几乎没有相似的实体记录会被发现。因此，本文使用局部敏感哈希预处理步骤对属性表示模型降维，既可以减少传统属性匹配归纳法的复杂度，同时保证了属性对分区的质量。

局部敏感哈希算法(LSH)可以减少高维度空间的维数，并且保证相似度不变，来减少属性值比较的数量。使用属性表示模型和Jaccard相似度，Min-hashing和banding方法来降低比较所有可能匹配的属性对的复杂度。

属性模型表示为一个矩阵，其中每个列都是属性a_j的向量T_j。在这个矩阵的行中，一个列的Min-hash值是该列首次出现在序列中元素的位置。因此，用n个哈希函数对行进行交换，产生含有n个Min-hash值的向量；这个向量叫做Min-hash签名。在交换序列后两列中产生相同的Min-hash值的概率等于Jaccard的相似度；因此，Min-hashing保留了变换矩阵的相似度，从而减少了表示属性的向量的维度。然而，即使Min-hash签名的数量相对较小，但是计算所有可能签名对的相似度的复杂度也较高；因此，可以将这些签名划分为很多个bands，在至少一个band上Min-hash值相同的签名被认为是候选配对的，并作为属性匹配归纳算法的输入(适用于迭代只有通过这些候选配对代替所有可能的属性对)。

将n个Min-hash值作为签名，分为b个band，并且令 $r=n/b$ 行Min-hash值为一个band， $s^r$ 表示两个band相同的概率， $1-s^r$ 表示两个band不相同的概率，每一个band都不相同的概率是 ${\left(1-s^r\right)}^b$ ，则两个属性在至少一个band上完全相同的概率是 $1-{\left(1-s^r\right)}^b$。这个函数具有S型曲线特征，拐点代表的是相似性的阈值。这个阈值可以近似为 ${\left(1/b\right)}^{1/r}$。例如，选择b = 30和r = 5，只需要对具有Jaccard相似度大于~0.5的属性对进行属性聚类(示例图3)。这样就减少了属性对之间求相似度的计算复杂度。

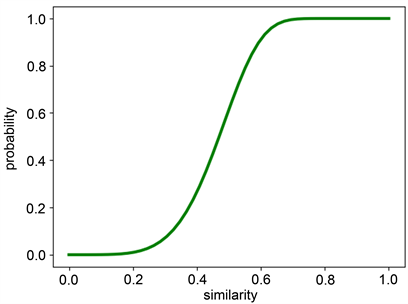
Figure 3. LSH s curves of r = 5 and b = 30. The arrow represents the estimated threshold

图3. r = 5和b = 30的LSH s曲线。箭头表示估计的阈值

4.2.2. 松散属性匹配归纳法

本文4.2节中属性匹配归纳法加以改进，松散属性匹配归纳法主要由下面四个步骤组成：属性值标记化；基于局部敏感哈希预处理后的二进制属性表示模型；相似度测量采用Jaccard系数；算法1用来作为改进后的聚类算法。

算法1：属性聚类算法

输入：基于局部敏感哈希处理后的属性表示模型A₁、A₂

输出：一个聚类结果：K

1) edges←{}sim←Map

2) Max←Map Cand←Map

//属性匹配最大相似度

3) foreach $a_i\in A_1$, $a_j\in A_2$ do

4) sim←( i,a _j>,similarity( ${\tau }_i,{\tau }_j$ ))

5) if Sim.get( i,a _j>) > Max.get(a _i) then

6) Max←(a_i,sim)

7) if Sim.get( i,a _j>) > Max.get(a _j) then

8) Max←(a_j,sim)

//属性匹配，找出候选集

9) foreach $a_i\in A_1$, $a_j\in A_2$ do

10) if Sim.get( i,a _j>) ≥ (a∙Max.get(a _i)) then

11) Candidates←(a_i,a_j)

12) if Sim.get( i,a _j>) ≥ (a∙Max.get(a _j)) then

13) Candidates←(a_j,a_i)

14) foreach $a_i\in A_1$ ， $a_j\in$ Candidatesget(a_i) do

15) if $a_i\in$ Candidatesget(a_j) then

16) edges← i,a _j>

17) K←getConnectedComponentsGrThan1(edges)

return K

上述算法1首先计算出两个数据源中所有可能匹配的属性之间的相似度，以及它们的最大相似度值(第2~8行)。第4行使用Jaccard系数作为相似度度量。在第9~13行使用松散的属性匹配归纳法来找出属性的候选匹配集，根据阈值来判断最相似的属性(例如：0.9.maxSimValue)。如果一个属性 $a_i$ 在它的候选匹配对象中有属性 $a_j$ ，那么边 $\langle a_i,a_j\rangle$ 被收集(第14~16行)。最后，用这些边构建基数大于1的图连通分量，表示为聚类(第17行)。选择使用多节点聚类可以收集所有属性，也就是可以确保包含所有可能的标记(模块键)。

4.3. 松散模式感知元分块方法

本节描述了基于图的模式感知元分块技术中的两个步骤。在第一步中，分块图 $G_{\beta }\left\{V_{\beta },E_{\beta },W_{\beta }\right\}$ 使用

聚合熵来对边进行加权来表示在块中出现的实体记录的相关性。第二步是一个新的修剪标准，来去除块中多余的比较。

4.3.1. 分块图加权

以图1中图1(a)和图1(b)为例子，通过标记分块之后派生出的元分块图如图5，图中每个边的权值表示的是在标记分块图中相似记录出现的次数，将权值小于一定阈值的边修剪后得到图5(b)，但是仍然有

多余的两条边 $e_{p_1-p_2}$ 和 $e_{p_3-p_4}$ 没有被去掉。

为了解决图4问题。采用了属性匹配归纳法之后的相关属性组，消除了“中体奥林匹克花园”的不同的语义，将“中体奥林匹克花园”相关的块划分为两个新块，一个指地块，一个指项目名称，从图5(a)

中可以看出边 $e_{p_1-p_2}$ 和 $e_{p_3-p_4}$ 的权值都降低了。在元分块图5(b)中更改了全局阈值后正确地删除了一个多余的边( $e_{p_1-p_2}$ )。提高了精确度，并且保持了召回率。但是仍然存在一个多余的比较( $e_{p_3-p_4}$ )。

Figure 4. (a) Derived module partition diagram; (b) Reconstructed block diagram: dotted lines represent trimmed edges, and red indicates that redundant comparisons have not been removed

图4. (a) 派生的模块划分图；(b) 重构的分块图：虚线表示修剪的边，红色表示多余的比较没有被去掉

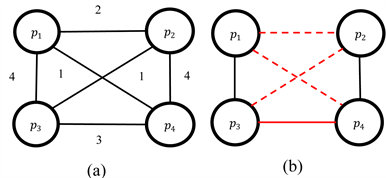
Figure 5. Disambiguation effect of the module partitioning key on the meta-block

图5. 模块划分键在元分块上消除歧义的效果

为了消除这个多余的比较，本文使用4.1.1节中介绍的信息熵来描述在属性匹配归纳之后重新生成的每个属性聚类。在该方法中，分块键的重要性与它得到的属性熵成正比。为此，通过计算聚合熵，得到了每组属性的熵值。一组属性 $C_k$ 的聚合熵的定义是：

$\bar{H}\left(C_k\right)=\frac{1}{\left|C_k\right|}\cdot \underset{A_i\in C_k}{{\displaystyle \sum }}H(Aj)$

将模式不可知的分块方法(如标记分块)与属性匹配归纳法相结合时，每个分块键 $b_i$ 都与一个聚类 $C_k$ 唯一相关联，即 $b_i\to C_k$。在图1(b)中“中体奥林匹克花园”，消除在不同数据源中语义不同的问题后，可以将它划分为聚类 $c_1$ 的中分块键“中体奥林匹克花园_c1”，以及聚类 $c_2$ 中的分块键“中体奥林匹克花园_c2”； $c_1$ 指的是项目名，而 $c_2$ 指的是实体概要中的地址。如图5中对“中体奥林匹克花园”进一步分块后，每一组分块键 ${\beta }_j$ 关联的熵 $h\left({\beta }_j\right)$ ：

$h\left({\beta }_j\right)=\frac{1}{\left|{\beta }_j\right|}\cdot \underset{b_i\in {\beta }_j}{{\displaystyle \sum }}h(bi)$

$h\left(b_i\right)=\bar{H}\left(C_k\right)$ 是与一个分块键 $b_i\to C_k$ 相关联的熵。

为了表述两个实体概要 $p_u$ 和 $p_v$ 之间的权重，在表2中显示了在给定块集合中描述实体 $p_u$ 和 $p_v$ 的联合概率分布的统计表。例如：单元格 $n_{12}$ 代表了在 $p_v$ 不存在 $p_u$ 存在时的块数量(没有 $p_v$ 表示为“ $\neg$ ”)；单元 $n_{2+}$ 表示 $p_u$ 不存在的块的数量(独立于 $p_v$ )。这些值也称为观测值。括号中的值是从图1(b)的块集合中派生出来的值，这里以实体概要 $p_1$ 和 $p_3$ 为例。利用皮尔森的卡方(chi-squared)测试( ${\chi }^2$ ) [12] 来判断分块内的 $p_u$ 和 $p_v$ 的独立性；即，测试 $p_u$ 的分布在块(表的第一行)中存在时， $p_v$ 的分布是否与 $p_u$ 不存在的情况下(表中的第二行) $p_v$ 的分布相同。在实践中，卡方(chi-squared)测试测量了假设 $p_u$ 和 $p_v$ 在块中独立出现时，观测到的( $n_{ij}$ )和预期( $u_{ij}$ )样本数(对于 $i=1,2;j=1,2$ )之间的偏差。因此，统计表的每个单元的预期值是： $u_{ij}=\left(n_{i+}\cdot n_{+j}\right)/n_{++}$。

Table 2. Associated tables of p u , p v

表2. $p_u$ 、 $p_v$ 关联表

因此，表示实体概要的节点 $p_u$ 和 $p_v$ 节点之间的权值 $W_{uv}$ 是按照如下公式计算的：

$W_{uv}={\chi }^2\cdot h\left({\beta }_{uv}\right)=\underset{i\in \left\{1,2\right\}}{{\displaystyle \sum }}\underset{j\in \left\{1,2\right\}}{{\displaystyle \sum }}\frac{n_{ij}-u_{ij}}{u_{ij}}\cdot h\left({\beta }_{uv}\right)$

最终求得每个边的权值如图9(b)所示。

4.3.2. 图修剪

事实上，当使用基于边数的阈值选择时，就会出现以下问题。以权值的平均值为标准。

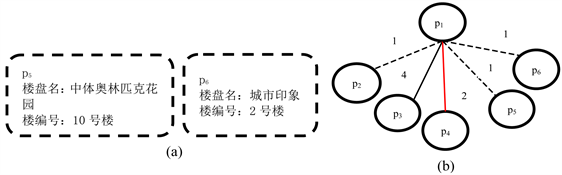
Figure 6. (a) Two additional entity profiles; (b) The block diagram representation centered on node p₁

图6. (a) 两个额外的实体概要；(b) 为节点p₁为中心的分块图表示

以图6中为例。图6(b)显示了 $G_{p_1}$ ，以节点实体概要 $p_1$ 为中心。如果实体集合(如图1(a))仅由实体概要集 $\left\{p_1,p_2,p_3,p_4\right\}$ 组成，生成的图 $G_{p_1}$ 只有4个节点和3条边。在这个场景中，边权值(本地的修剪阈值)的平均值略大于2。因此，只有在修剪阶段保留了 $p_1$ 和 $p_3$ 之间的边界。但是，如果将图6(a)中的两个实体概要添加到实体集合中，则将两个节点和两个边添加到 $G_{p_1}$ 中。这将使阈值变为1.8。因此，在修剪阶

段保留了 $p_1$ 和 $p_4$ 之间的边界。为了防止图剪枝步骤中受到边数的影响，本文提出了一个权值节点修剪(WNP)中的阈值选择策略。

基本思想：首先确定每个节点的阈值，在以节点为中心的分块图中，具有最高权值的边代表着分块和加权函数组合的相似度上限；因此，本文选择一个与相邻边数无关的阈值，考虑这个上界的一小部分：

$\overline{{\theta }_i}=\frac{M}{c}$ ，在这里M是最大的权值，c是任意常数。在真实数据集中显示为具有有效性的c值是c = 2；

c值越高实现更高的召回率(PC)，但代价是牺牲精准度(PQ)。

确定了每个节点的本地阈值后，执行的最后一个步骤是保留边。不过，在以节点为中心的修剪中， $p_i$ 和 $p_j$ 之间的每一个边 $e_{ij}$ 都与两个阈值有关： ${\theta }_i$ 和 ${\theta }_j$ ； ${\theta }_j$ 和 ${\theta }_j$ 分别是与 $p_i$ 和 $p_j$ 相关的阈值。因此，如图7(b)所示，每条边 $e_{ij}$ 都有一个权值：(i)小于 ${\theta }_i$ 和 ${\theta }_j$ ，(ii)大于 ${\theta }_i$ 和 ${\theta }_j$ ，(iii)小于 ${\theta }_i$ 和大于 ${\theta }_j$ ，或(iv)大于 ${\theta }_i$ 和小于 ${\theta }_j$。案例(i)和(ii)并不模糊，因此 $e_{ij}$ 在第一个案例中被丢弃，并保留第二个案例。但是，案例(iii)和(iv)是不明确的。

现有的元分块论文提出的两种不同的解决这种歧义的方法：重新定义WNP(wnp1)：如果它的权值

超过了两个阈值中的一个，就会保留 $e_{ij}$ (wnp1)，相对的WNP(wnp2)为：如果它的权值大于 ${\theta }_i$ 和 ${\theta }_j$ ，那么就保留它的边界。本文中使用唯一的通用阈值，等于： ${\theta }_{ij}=\left({\theta }_i+{\theta }_j\right)/d$ ，d是一个常数；对于d = 2，所得到的阈值 ${\theta }_{ij}$ 等于两个相关的本地阈值的平均值，如果大于该阈值则保留它的边界。

如图7修剪阶段之后的在图8(c)中显示最后一个模块划分图。多余的边 $e_{p_3-p_4}$ 现在已经被正确地移除。

Figure 7. Weight threshold: the oriented edge from $p_i$ to $p_j$ indicates that the weight of the edge of $e_{ij}$ is higher than that of theta ${\theta }_i$ ; A directed edge from $p_j$ to $p_i$ indicates that the weight of the $e_{ij}$ edge is higher than that of the ${\theta }_j$

图7. 权重阈值：从 $p_i$ 到 $p_j$ 的定向边表明了 $e_{ij}$ 的边的权值比 ${\theta }_i$ 高；从 $p_j$ 到 $p_i$ 的一个有向边表明， $e_{ij}$ 边的权值比 ${\theta }_j$ 高

Figure 8. Effect of attribute entropy information on element partitioning

图8. 属性熵信息对元分块的影响

5. 实验评估

5.1. 数据集

本文采用“面向领域的Web数据抽取”项目所抽取到的多个数据源的房地产数据进行实验。抽取到的数据如下表3所示。

Table 3. Statistics of information extracted from real estate

表3. 房地产抽取信息量统计

5.2. 实验方法

本文采用三种分块方法进行实体解析实验(见表4)。

Table 4. Blocking methods

表4. 分块方法

5.3. 实验结果及分析

分别从沈阳市的楼盘表、楼栋表、户型表中抽取10,000条数据进行标注，再从各标注数据表中抽取3000条数据，重复数量分别为606,396,511。

评价指标：本文采用精确度(precision)、召回率(recall)、F₁-score，对实验结果进行评估分析。精确度(P)是分块正确的正例数量占所有分为正例的百分比，召回率(R)是分块正确的正例数量占实际正例数量的百分比，F₁-score是它们的调和均值。

通过表5，可以看出，三个表中标记分块方法效果最差，松散模式感知元方法效果最好，采用松散模式感知元分块方法很大程度的提高了实体解析的效率。本文中的模式感知的元分块方法在标记分块的基础上，保证了召回率的同时，显著的提高了比较的准确率。通过图9可以看出，三个表中标记分块方法的比较次数最大，而采用松散模式感知元分块方法的比较次数最小，很大程度的减少了比较次数，提高了实体解析效率。

Table 5. Experimental results

表5. 实验结果

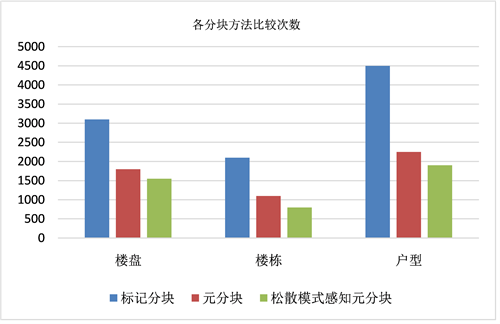
Figure 9. Number of blocking comparisons

图9. 分块方法比较次数

6. 结束语

在Web大数据集中进行实体解析操作时，由于数据量较大，采用直接比较的方法会导致算法复杂度较高，所以这里采用了基于聚合熵加权图的元分块的方法，降低比较的次数，又由于处理不同数据源，模式不同，所以采用了基于局部敏感哈希的属性匹配归纳法对属性空间划分，本文结合上述两种方法，对多数据源中数据进行实体解析，减少了算法中大量冗余和多余的比较，提高了算法的效率，通过实验表明，该方法的效果明显优于传统的模式未知的标记分块方法，在保证召回率的同时，提高了精确度。