1. 引言
随着智能时代的到来,机器学习领域越来越广泛受到社会青睐,成为很多学者的研究热门。2001年Lee等人通过对支撑向量机的深入研究首次使用了sigmoid积分函数
对无约束的支撑向量机(Support Vector Machine, SVM) [1] 进行光滑化,这是首次在支撑向量机中引入光滑的概念。得出了光滑支撑向量机(Smooth Support Vector Machine, SSVM) [2] 模型,然后在Armijo线搜索的基础上采用了牛顿算法对此光滑支撑向量机模型进行求解,结果展现出了比一般的支撑向量机模型更好的分类性能,同时也提高了其计算的效率。同年Mangasarian等人也提出了RSVM (Reduced Support Vector Machine) [3],将模型研究的约束凸优化问题改进为无约束强凸优化问题,从而使相应算法在求解问题上提升了一定的速度,尽管该模型在实际过程中对于一些大规模数据问题的求解所花费的时间比较长,且需要保存的信息和计算量也比较多,在求解思路上,仍是一种主流的进步方法。从此越来越多的学者们逐渐将研究光滑函数作为SSVM模型的核心,并以此开辟了支撑向量机的一个新的研究方向。
2005年,袁玉波 [4] 等人提出了两个多项式光滑函数,通过对支撑向量机模型的无约束目标函数进行光滑化处理,引出了PSSVM模型,也证明了PSSVM相比SSVM而言有着更好的分类性能。之后又提出了三阶样条光滑函数 [5],从而引出了新的支撑向量机的TSSVM模型。通过分析TSSVM模型的收敛性和对应数据实验结果可以说明TSSVM有着更优秀的分类效果。2008年,熊金志等人 [6] 更是提出了高于三阶样条光滑函数一个数量级的六阶光滑函数。
随着光滑函数逼近正号函数的精度的提高,显然其函数本身也变得越来越复杂,这并不利于科学计算。本文主要介绍了一种新的一致光滑逼近函数来替代正号函数。克服了支撑向量机模型求解过程中出现的不可微性,并基于此一致光滑逼近函数设计了相应算法,通过理论计算并证明了该光滑函数的收敛性,最后通过数值模拟体现了该函数在光滑支撑向量机模型中的求解精度、效率和推广适应性的优越性能。
2. 光滑支撑向量机
2.1. 支撑向量机
对于给定一组数据
其中
,我们的目标是从数据中寻求一个假设函数
,使得
,即
(1)
更进一步,线性二分类模型认为假设函数的形式是基于对特征
的线性组合,即
(2)
其中
。
定义1. 线性二分类模型的目标是找到一组合适的参数
,使得
(3)
即,线性二分类模型希望在特征空间找到一个划分类别的超平面,将属于不同标记的样本分开。证明
(4)
由于能将样本分开的超平面有可能有很多,故SVM希望能找到一个离各个样本都比较远的划分超平面,即最优超平面。
当面对样本的随机扰动时,离各个样本都较远的划分超平面抗干扰的能力比较强,我们希望在优化间隔的同时,允许分类错误的样本出现,但这类样本应尽可能少:
(5)
其中,
是指示函数,C是个可调节参数,用于权衡优化间隔和少量分类错误样本这两个目标。但是,指示函数不连续,更不是凸函数,使得优化问题不再是二次规划问题。所以我们需要对其进行简化。
公式(5)难以实际应用的原因在于指示函数只有两个离散取值0/1,对应样本分类正确/错误。为了能使优化问题继续保持为二次规划问题,我们需要引入一个取值为连续值的变量,刻画样本满足约束的程度。我们引入松弛变量
,用于度量样本违背约束的程度。当样本违背约束的程度越大,松弛变量值越大。即
(6)
定义2. (软间隔支撑向量机基本型)软间隔支撑向量机旨在找到一组合适的参数
使得
(7)
其中,C是个可调节参数,用于权衡优化间隔和少量样本违背大间隔约束这两个目标。当C比较大时,我们希望更多的样本满足大间隔约束;当C比较小时,我们允许有一些样本不满足大间隔约束。
定义 3. (软间隔支持向量机对偶型)软间隔支持向量机的对偶问题等价于找到一组合适的
,使得
(8)
2.2. SSVM
由软间隔支撑向量机的原始型和对偶形式我们可以对其进行求解得到
,于是分类函数
(9)
其中,
令
,
则问题(7)改写为
(10)
对于任何核函数,上式均是个凸二次规划问题,不妨取
,同时用b衡量分类间隔(
),
于是在对偶问题中
,同时让松弛变量
最小,则(10)转化为
(11)
由约束条件知,
这里是非光滑的。将其代入问题(11),得到一个强凸无约束优化问题:
(12)
有唯一解。
令
,
是核矩阵
的第i行。则将(13)改写为一般形式为
(13)
用不同的光滑函数来近似逼近正号函数
,可得不同的SSVM模型,典型的光滑函数有sigmoid函数的积分函数、多项式函数、样条函数和插值函数等等。
这里我们假定一个光滑函数
来近似
,则得到光滑支撑向量机SSVM:
(14)
即为常见的光滑支撑向量机模型。
3. 一致光滑逼近函数及其性质
基于对正号函数的逼近的考虑,我们寻找了一致光滑逼近函数来光滑目标函数中的不可微部分,利用一致光滑逼近函数来近似绝对值函数,从而通过新问题的求解来逼近原问题的解。
给出的一致光滑逼近函数如下所示:
,
(15)
当
时, 。
。
该函数是由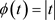 的两个一致光滑逼近函数
的两个一致光滑逼近函数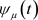 和
和 [7] 的凸组合得到,其中
[7] 的凸组合得到,其中
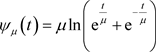 ,
, ;
;
 ,
, .
.
利用pycharm,采用精度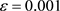 ,
,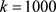 ,在区间
,在区间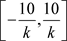 上一致光滑逼近函数
上一致光滑逼近函数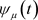 和
和
及其凸组合形式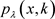 分别与正号函数
分别与正号函数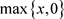 的逼近程度见图1,从图中可以看出,其凸组合形式的光滑函数
的逼近程度见图1,从图中可以看出,其凸组合形式的光滑函数 因其参数的选择不同可以有更好的适应性。
因其参数的选择不同可以有更好的适应性。

Figure 1. The approximation degree of smooth functions
图1. 不同光滑函数的逼近程度
记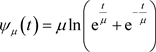 ,
,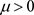 为
为 的上方一致光滑逼近函数,
的上方一致光滑逼近函数,
则:1) ;
;
2)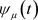 的值随参数
的值随参数 的减小而单调下降,且当
的减小而单调下降,且当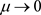 时,
时,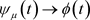 ;
;
3) ,且
,且 。
。
证明1) 
由于
从而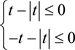 且
且 与
与 中至少有一个等于0,因此
中至少有一个等于0,因此

即
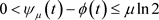
2)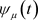 的值随参数
的值随参数 的减小而单调下降的证明可参考于李兴斯等 [8] [9] 关于凝聚函数的性质推导过程。结合
的减小而单调下降的证明可参考于李兴斯等 [8] [9] 关于凝聚函数的性质推导过程。结合 ,即
,即 ,这表明
,这表明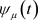 有界,利用单调有界必有极限的定理及夹逼准则,则有
有界,利用单调有界必有极限的定理及夹逼准则,则有 。
。
3)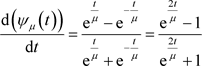 ,而
,而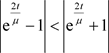 ,即
,即 ,因此
,因此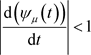 ,且
,且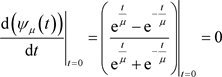 。
。
我们给出了 时该函数与绝对值函数的逼近情况如图2。
时该函数与绝对值函数的逼近情况如图2。
记 ,
, 为
为 的下方一致光滑逼近函数,
的下方一致光滑逼近函数,
则:1)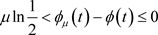 ;
;
2) 的值随参数
的值随参数 的减小而单调递增,且当
的减小而单调递增,且当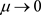 时,
时, ;
;
3)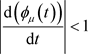 ,且
,且 。
。
证明1) 由于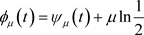 ,于是
,于是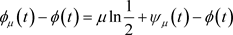 ,结合上文中叙述的
,结合上文中叙述的
 ,则有
,则有

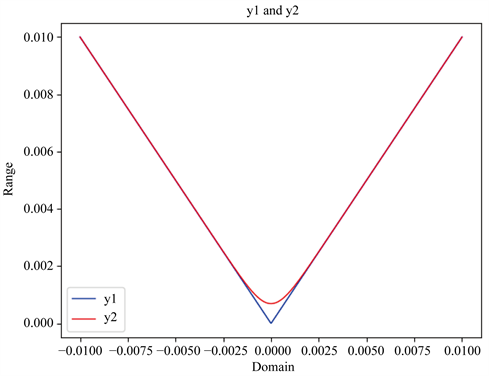
Figure 2. The approximation degree of y1 and y2
图2. 光滑函数y2与绝对值函数y1的逼近程度
2)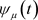 的值随参数
的值随参数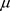 的减小而单调递增的证明可参考于杨庆之等人 [10] [11] 等关于凝聚函数法的文献。
的减小而单调递增的证明可参考于杨庆之等人 [10] [11] 等关于凝聚函数法的文献。
结合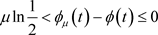 ,即
,即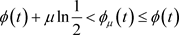 ,这表明
,这表明 有界,利用单调有界必有极
有界,利用单调有界必有极
限的定理及夹逼准则,则有 。
。
3) ,而
,而 ,即
,即 ,因此
,因此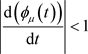 ,且
,且 。
。
我们给出了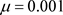 时该函数与绝对值函数的逼近情况如图3。
时该函数与绝对值函数的逼近情况如图3。
以上得到的两个一致光滑逼近函数均可以用作近似逼近正号函数 ,然而其精度并不是很好,基于凸组合的特殊线性组合原理,从而将是由
,然而其精度并不是很好,基于凸组合的特殊线性组合原理,从而将是由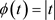 的两个一致光滑逼近函数
的两个一致光滑逼近函数 和
和 的凸组合而得到的新的函数:
的凸组合而得到的新的函数:
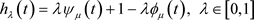
而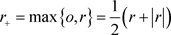 于是
于是

从而相应的光滑函数为
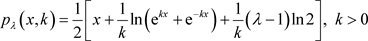 (16)
(16)

Figure 3. The approximation degree of y1 and y3
图3. 光滑函数y3与绝对值函数y1的逼近程度
对于这样一个新的凸组合光滑逼近函数,将其与绝对值函数进行比较如图4所示。
当 ,
, 时
时
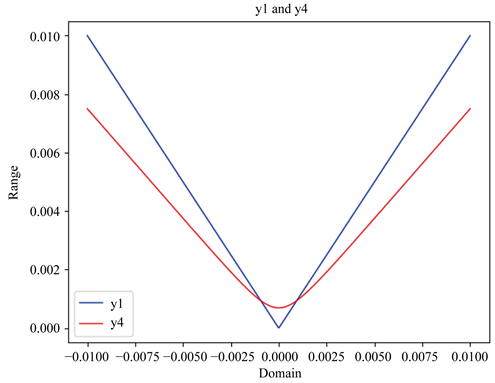
Figure 4. The approximation degree of y1 and y4
图4. 光滑函数y4与绝对值函数y1的逼近程度
当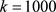 ,
,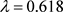 时,见图5。
时,见图5。
对于给定的光滑因子k,
当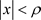 时,逼近程度
时,逼近程度
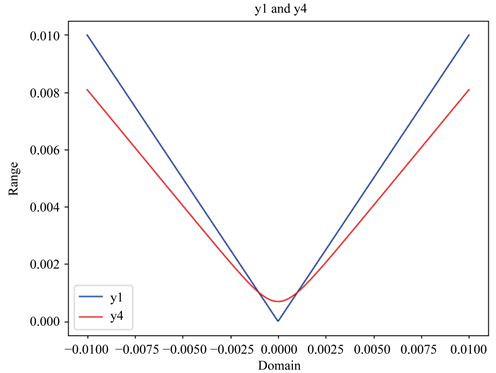
Figure 5. The approximation degree of y1 and y4
图5. 更新后的光滑函数y4与绝对值函数y1的逼近程度
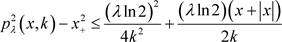
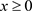 时,逼近程度
时,逼近程度
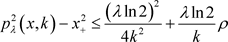
故当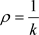 时,
时,

故当 时,
时,
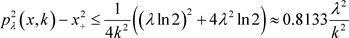
故当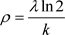 时,
时,
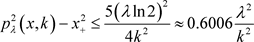
 时,逼近程度
时,逼近程度

显然,只需取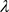 为趋向于0的合适的值我们即可得到较强的逼近精度。对于任意一个
为趋向于0的合适的值我们即可得到较强的逼近精度。对于任意一个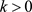 ,问题(14)和(15)的解的逼近精度始终满足于
,问题(14)和(15)的解的逼近精度始终满足于

其中 。
。
要求SSVM的解满足精度要求。只要使得 ,只需有
,只需有

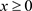 时,
时,
故当 时,解得
时,解得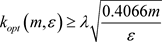
当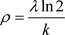 时,解得
时,解得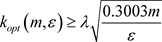
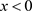 时,解得
时,解得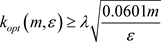
4. Newton-Armijo算法
Newton-Armijo算法是对于牛顿法的一个改进。采用Armijo线搜索,并利用牛顿法进行求解。记式(13)的目标函数梯度为
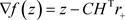 ,
,
使用光滑函数 代替
代替 得到:
得到: ,其中(
,其中( 是k取定值时的
是k取定值时的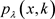 )
)
Hessian矩阵 ,其中
,其中 ;式(15)的目标函数梯度为:
;式(15)的目标函数梯度为:
 ,
,
Hessian矩阵 ,其中
,其中
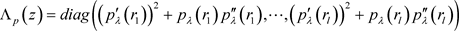
一般的Newton-Armijo算法
目标函数的下降方向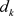 由方程
由方程 求得,由于使用了Armijo一维搜索,保证了目标函数值在迭代过程中的不断下降,其具体步骤如下:
求得,由于使用了Armijo一维搜索,保证了目标函数值在迭代过程中的不断下降,其具体步骤如下:
Step 1
Initialization. Given the initial point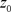 , let
, let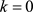 ,
,  , parameter:
, parameter: 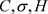 generated from the input data;
generated from the input data;
Step 2
Calculate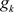 . If
. If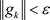 , stop; or turn to step 3;
, stop; or turn to step 3;
Step 3
Calculate Hessian matrix , solve
, solve 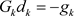 and then we get
and then we get ;
;
Step 4 (Armijo line search) select

and let
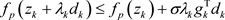
Step 5
Let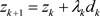 ,
, 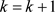 , turn to step 2.
, turn to step 2.
该算法每次迭代需要计算Hessian矩阵 ,再确定搜索方向,所需要的工作量相当大,并且由于数据的特征比较多,相应的对于Hessian矩阵的计算就会变得比较复杂。
,再确定搜索方向,所需要的工作量相当大,并且由于数据的特征比较多,相应的对于Hessian矩阵的计算就会变得比较复杂。
改进的Newton-Armijo算法
将问题(13)中的目标函数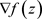 光滑为
光滑为 ,令
,令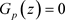 ,然后求解该方程,由于
,然后求解该方程,由于 中
中
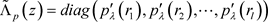
比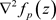 中
中 简单,因而这个改进的方法在计算起来速度更快。其具体步骤如下:
简单,因而这个改进的方法在计算起来速度更快。其具体步骤如下:
Step 1
Initialization. Given the initial point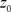 , let
, let ,
, 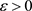 , parameter:
, parameter: 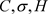 generated from the input data;
generated from the input data;
Step 2
Calculate . If
. If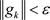 , stop; or turn to step 3;
, stop; or turn to step 3;
Step 3
Calculate Hessian matrix , solve
, solve  and then we get
and then we get ;
;
Step 4 (Armijo line search) select
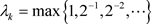
and let

其中 ,而
,而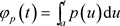 (a是
(a是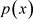 的定义域下界),因为
的定义域下界),因为 的一阶
的一阶
充分必要条件是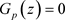 ;
;
Step 5
Let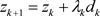 ,
,  , turn to step 2.
, turn to step 2.
5. 数值结果和比较
5.1. 一致光滑牛顿法求解
数值实验数据来自用python编写的随机线性不可分数据集,统共样本数据有1000样本,测试样本有300个,每个样本有30个特征,采用了高斯核来将其映射到高维特征空间上得到分类结果如图6~9。
可以看出在小规模数据集下其分类的正确率都有着良好的性质。基于此结果的影响下,我们采用了其他数据集,例如区分数字的分类数据集USPS,我们实验选取了5000个训练样本,1800个测试样本,每个样本有着160个特征,在精度要求 的情况下使用不同Newton-Armijo算法求解算法下分类所需的迭代次数、时间、训练错误率和测试错误率如表1所示。
的情况下使用不同Newton-Armijo算法求解算法下分类所需的迭代次数、时间、训练错误率和测试错误率如表1所示。
5.2. 分析与比较
由图表中数据进行分析可知,我们得到一些关于不同光滑函数与算法的结合求解SVM的相关结论:
1) 一般来说,随着光滑函数与目标函数的逼近程度的靠近,求解SVM的解的精度会更好,在迭代次数有要求的情况下,光滑函数的选取决定了它是否能够满足实验精度要求,否则只能在最大迭代次数下才能得到满足实验精度的结果。新选取的光滑函数的参数选择也决定了它是否能够很好的契合实际问

Figure 6. The result (1) of classification
图6. 分类结果(1)
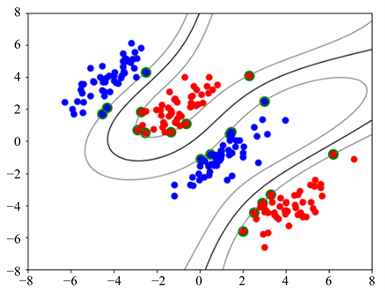
Figure 7. The result (2) of classification
图7. 分类结果(2)

Figure 8. The result (3) of classification
图 8. 分类结果(3)
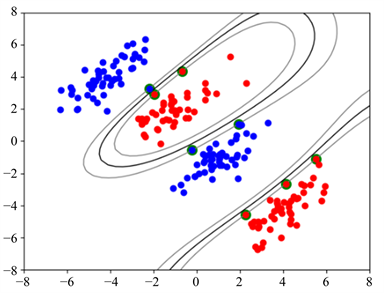
Figure 9. The result (4) of classification
图9. 分类结果(4)

Table 1. Experimental results of different solving algorithms for different smooth functions
表1. 不同光滑函数求解算法的实验结果
题的解决思路。在这方面,凸组合形式的光滑函数给了我们一些新的想法,在逼近程度上与求解问题精度上做一个很好的平衡是一个好的思路。
2) 一般来说,光滑函数的逼近可以使得训练错误率的下降逐渐减小甚至为0,但是数据训练的时间也会越来越多。这就要求我们在求解大规模问题中需要寻求一个适应性很好的光滑函数,在光滑函数的逼近程度和函数本身的复杂中间需要我们做好平衡,如何保证在尽量减少计算量的情况下最大化计算效率和求解速度,并在算法参数和光滑参数的结合上做一个好的调整是一件值得考虑的事情。
6. 结论
综上可知,支撑向量机的光滑算法中,光滑函数的不同对于算法的使用有着不同的收敛速度及计算复杂度,很明显改进后的改进的Newton-Armijo算法的收敛速度优于一般的Newton-Armijo算法;尽管是同样的算法中实验,光滑函数的不同对于结果也有着不同的影响,其影响程度也与光滑函数的逼近程度相关,越逼近正号函数的模型,其解的精确度就越高,训练结果达到的正确率也就越高,但是其训练时间也就随之增加。今后待研究问题方向有:除却Newton-Armijo算法之外的BFGS-Armijo算法、Newton-PCG等其他算法在不同光滑函数的模型下求解SSVM模型的收敛速度及求解精确度的问题、在大规模数据中处理数据训练时间和精度的平衡、光滑算法的优化改进等等。
NOTES
*第一作者。
#通讯作者。