1. 引言
在小波理论之后又新发展起一种理论,即框架理论。小波框架是由多种数学学科结合得来的,1952年,框架理论是首先由Duffin以及Schaeffer给出。我们要说的框架就是一种具有Riesz基性质的基,但是却不一定是基,也可以认为它是这一种广义的基。
最小能量小波框架 [1] [2] [3] [4] [5] 的优点在于可以避免信号在分解以及重构时,对于对偶框架的寻找,也简化了计算过程的繁杂性,并且还能最大可能地去保证数值的稳定性。在框架多分辨分析(FMRA)的基础上,2000年,由C.K. Chui以及W. He首先给出了最小能量小波框架。
2. a尺度二元最小能量多小波框架的概念
先给出文章要提到的记号:
,
,
里函数的内积和Fourier变
换定义如下
其中
。
定义向量值函数
,平移算子为
,伸缩算子为
。
定义1 [6] 假设有正常数
,使函数族
能够满足
那么称函数族
是
的一个紧框架 [7] [8],A,B是这个框架的上,下框架界。当
时,有下列重构公式
(1)
那么称
是
的Parseval框架。
记
是
在
上的闭包。
定义2 [9] 假如每一个
是
的闭子空间,而且有
使得
满足
(1)
;
(2)
;
(3)
;
(4)
;
(5)
使
为
的紧框架,那么
是FMRA,其中
是FMRA的二
元尺度函数。
定义3 若
由
生成。设函数族
符合(3.1.1),且
,那么称
生成对应
的小波紧框架。
定义4 [10] 若
,而且
在原点处连续,对于
,如果一个函数族
符合
(2)
则称
是与
相对应的二元最小能量多小波紧框架。其中
式(2)等价于
(3)
若函数
满足
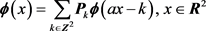 (4)
(4)
称上式为r重多尺度函数。此处 为
为 重矩阵序列。
重矩阵序列。
对式(4)两边施行Fourier变换有
 (5)
(5)
其中
 (6)
(6)
 为
为 的符号函数。对于
的符号函数。对于 根据定义2,就有
根据定义2,就有
 (7)
(7)
其中 是
是 重矩阵序列,等式两边做Fourier变换有
重矩阵序列,等式两边做Fourier变换有
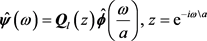
 为
为 的符号函数,表示为
的符号函数,表示为
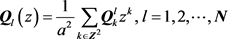 (8)
(8)
接下来利用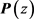 和
和 来构造一个
来构造一个 阶的分块矩阵
阶的分块矩阵
 (9)
(9)
 的共轭转置我们用
的共轭转置我们用 来表示。
来表示。
3. a尺度二元最小能量多小波框架的特征
定理1若 和
和 里都为Laurent多项式,并且
里都为Laurent多项式,并且 是
是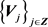 的尺度函数,则等价于
的尺度函数,则等价于
(1) 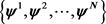 为与
为与 相应的二元最小能量多小波框架生成元;
相应的二元最小能量多小波框架生成元;
(2) 满足
满足
 (10)
(10)
(3)
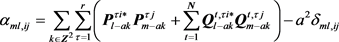 (11)
(11)
符合 且
且 是Kronecker符号为
是Kronecker符号为

证明:由式(4)和(7)以及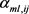 ,可以得到式(3)的等价式子
,可以得到式(3)的等价式子
 (12)
(12)
并且有,式(10)等价于
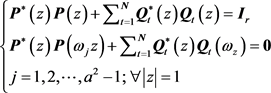 (13)
(13)
即有
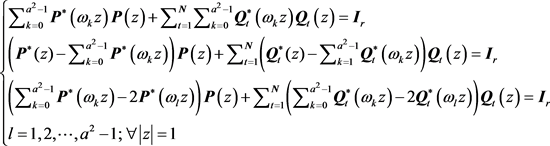
因为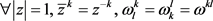 ,有
,有

那么上式也可以写为
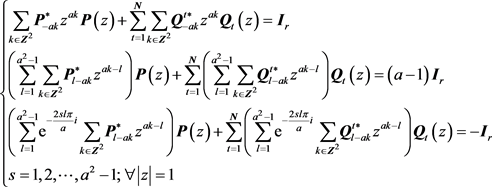
利用Cramer法则和Vandermonde行列式的性质可将上变形为

对上面式子中所有等式两边乘 ,有
,有

即为

对上式做Fourier逆变换就有

根据式(4)和(7),上式就可变形为
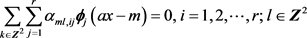 (14)
(14)
由(11)式证明得到式(14),也就有了(12)式,现在我们来证明由(12)式得到(11)式。
 是紧支撑函数,若固定m,则
是紧支撑函数,若固定m,则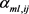 仅有有限个不为零,那么泛函
仅有有限个不为零,那么泛函

仅有有限个不为零。
接下来对(12)式做傅里叶变换有

由于 不是平凡函数,所以
不是平凡函数,所以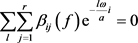 ,既有
,既有 ,故
,故
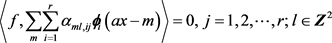
设 ,则有
,则有 ,最后做傅里叶变换就可得
,最后做傅里叶变换就可得 ,综上,定理得证。
,综上,定理得证。
定理2 若尺度函数 紧支撑,并有
紧支撑,并有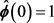 ,设
,设 是对应的二元最小能量多小波框架生成元,则
是对应的二元最小能量多小波框架生成元,则
 (15)
(15)
证明:由于 那么我们就可以得到
那么我们就可以得到 。下面只看式(15)中当
。下面只看式(15)中当 的情况,i为其他数值时证明过程类似。
的情况,i为其他数值时证明过程类似。
记 为
为 的第一行元素,将
的第一行元素,将 中剩下的记为矩阵
中剩下的记为矩阵 ,那么根据式(10)就有
,那么根据式(10)就有

由 是Hermitian矩阵,那么就有
是Hermitian矩阵,那么就有
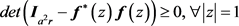
即有

其实
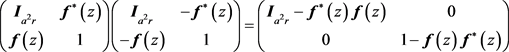
其中
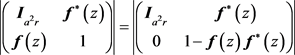

而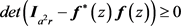 所以
所以 。
。
接下来将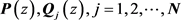 写为多相位形式
写为多相位形式
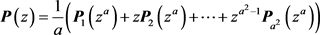

 阶的符号矩阵
阶的符号矩阵 中的每项都为Laurent多项式,记为
中的每项都为Laurent多项式,记为


那么就有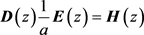 ,也即
,也即
 (16)
(16)
由式(10)有
 (17)
(17)
接下来讨论该框架存在的充分条件。
定理3 若多尺度函数为 ,且
,且 ,那么a
,那么a
尺度Laurent多项式符号函数符合
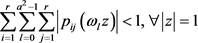
则存在二元多尺度函数 对应的二元最小能量多小波框架生成元
对应的二元最小能量多小波框架生成元 。
。
证明:由
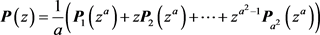
其中 是
是 的多相位矩阵。而由(16) (17)可以得到
的多相位矩阵。而由(16) (17)可以得到

即有

若 且有
且有 ,则
,则

根据Riesz定理可知,对于Laurent多项式 有
有

接下来把单位向量 按照文
按照文
献 [11] 里定理3的方式变换之后就可以得到 [11]

则

而且符合 。
。
4. 二元最小能量多小波框架的构造算法
对于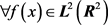 ,下面记
,下面记 ,
, 为
为 到子空间
到子空间 上的正交投影算子
上的正交投影算子

则根据以上算子式(3)可变形为
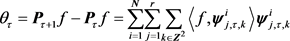 (18)
(18)
其中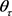 表示为误差项,还可以表示为
表示为误差项,还可以表示为
 (19)
(19)
那么由以上两式,做内积就可以得到
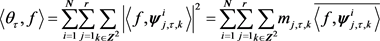
则
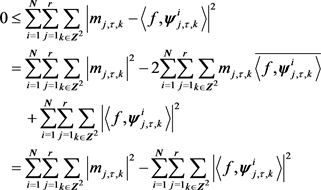
在式(19)下,误差项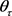 的系数能量是最小的,也正是这个原因我们把符合(3)的框架叫做最小能量小波框架。
的系数能量是最小的,也正是这个原因我们把符合(3)的框架叫做最小能量小波框架。
1) 分解算法 若已知 ,那么我们由
,那么我们由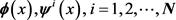 的加细方程我们可以得到
的加细方程我们可以得到
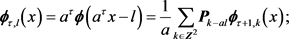

对以上两式两边与 作内积,就有以下分解公式
作内积,就有以下分解公式

2) 重构算法
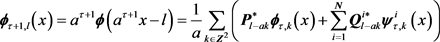
对上式两端与 作内积,就有
作内积,就有