1. 引言
博弈问题有三要素:博弈者、博弈策略和支付函数。经典博弈问题的支付函数值是一个单值的数或者向量。然而,受到一些不确定的因素与客观条件的影响,想精确计算出这个支付函数的函数值是比较困难的,通常只能得到一个值的大致范围。这样,支付函数就变成了一个集值函数。因此,研究集支付函数的向量均衡问题是非常有意义的。
有一些学者已经做了这方面的研究。文献 [1] 利用凸集分离定理研究了向量均衡问题的存在性。文献 [2] 提出了集值映射下向量均衡问题新的存在性定理。文献 [3] 研究了广义弱向量均衡问题的存在性结果。文献 [4] 在凸集和非凸集下,讨论了弱向量平衡问题的存在性。文献 [5] 研究了变分不等式问题在伪单调和不连续假设下的存在性结果。文献 [6] 研究了集值映射下的极大极小非均衡问题。文献 [7] 得到了一系列集值映射弱向量拟平衡问题解的存在性和连通性的结果。文献 [8] [9] 运用一些有利条件解决了一些非线性问题。
很少有文献研究集支付函数的向量均衡问题。向量均衡问题是指:
s.t.,
,
其中
,
,X和V是实Hausdorff拓扑线性空间,S是V中的一个尖闭凸锥。直接利用经典的方法讨论上述问题解的存在性定理所得到连续性假设中会涉及非开非闭集
,这使得相应的结果很难验证。在这篇文章中,利用经典的Fan-KKM定理与分离定理(包括凸集分离定理、非凸分离定理),在合理的假设下,分别研究了带有集支付函数的向量均衡问题解的存在性定理。
2. 预备知识
在整篇文章中,总是假设X和V是实Hausdorff拓扑线性空间,S是V中的一个闭的尖凸锥,并且
。
S的对偶锥
。
显然,
是单调增加函数(见文献 [2])。
集向量均衡问题(SVEP)是指:
,s.t.,
,
下面,给出拟上(下)半连续和S-拟上(下)半连续的定义。
定义2.1 设
是一个集值映射,
。如果对
,有
的邻域U,s.t.,
,
那么称F是
上的拟上(下)半连续;如果对
,F是S-拟上(下)半连续,那么称F是X上的S-拟上(下)半连续。
注1:这里所给出的定义与文献 [2] 中的定义不同,下面举例说明。
例1:设
是一个集值映射,
。F的定义如下:
取
,有
。由F的定义可知,一定存在0的邻域U,s.t.,
,
。即F在0点
-拟上半连续。
但在文献 [2] 中的定义2.1中却不满足,理由如下:
取
,
。显然,
,对0的任意邻域U,
。显然,F在0点不满足文献 [2] 中相应的概念。
引理2.1 设
是一个集值映射,F是X上的拟上半连续当且仅当它的上水平集是闭集,i.e.,对
,水平集
是闭集。
证明:一方面,假设
,
是闭集,要证F是X上的拟上半连续。由于
的补集
是开集,可知若对于
,有
则
。即
的邻域
,s.t.,
成立,得证。
另一方面,若F是X上的S-拟上半连续,要证
,水平集
是闭集。设
为
上的一个序列且
。假设
,那么
,根据拟上半连续的定义可知,存在实数N,当
时,有
,与假设矛盾。因此,
,水平集
是闭集。
下面,给出真S-拟凸和自然S-拟凸的定义。
定义2.2 [10] 设
是X上的非空凸集,
是一个集值映射,有下列定义:
1) 对
,并且
,有
或
,
则称集值映射F是真S-拟凸;
2) 对
,并且
,有
,
则称集值映射F是自然S-拟凸。
接下来,给出著名的KKM映象定义和Fan-KKM定理。
定义2.3 [11] 设
是一线性空间而且
,
是一多值映象,如果对任意有限集
有
,那么称F为KKM映象。
定理2.1 [11] 设X是一Hausdorff拓扑线性空间,
是X之一非空子集,
是Fan-KKM映象,再设
,
为X中的闭集,且至少存在一点
使得
是F中的紧集,则
。
最后,给出一类非线性标量化函数的定义以及性质。
定义2.4 [12] 设
和
,非线性标量化函数
为:
.
引理2.2 [13] 设
和
,有以下性质:
1)
;
2)
;
3) 如果
,那么
是单调递增的函数;
4) 若
,则
是严格单调递增的函数;
5)
是连续的函数。
3. 主要结论
在这一节,首先使用Fan-KKM定理以及非线性分离定理来证明下面结论:
定理3.1 设
和 ,
, 是X上的一个非空凸子集,
是X上的一个非空凸子集, 是一个集值映射,若满足下列条件:
是一个集值映射,若满足下列条件:
1) 对 ,
, 是X上的S-拟上半连续,
是X上的S-拟上半连续,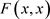 是S-拟下半连续;
是S-拟下半连续;
2) 对 ,
, 是
是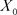 上的真S-拟凸;
上的真S-拟凸;
3) ;
;
则集向量均衡问题(SVEP)有解。
证明:首先,我们证明 ,
,
s.t. (3.1)
(3.1)
构造集值映象
 ,
, 
1) 对 ,都有
,都有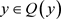 ,即
,即 ,
, 。
。
2) 又因为 为一个紧集,
为一个紧集, ,且
,且 是紧的,故仅需证
是紧的,故仅需证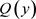 为闭集即可。
为闭集即可。
由Q的定义可知,
 ,
, 
再由F的连续性以及Q的定义可得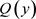 为闭集。
为闭集。
3) 下面证明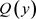 为一个KKM映象。
为一个KKM映象。
反证,若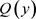 不是一个KKM映象,则
不是一个KKM映象,则 且
且 ,
, ,s.t.,
,s.t.,

由Q的定义得,
 ,
, 
由定义2.2以及 的单调性可知,
的单调性可知,
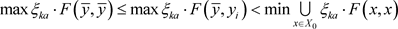
即,

由Q的定义得, 这与
这与 ,
,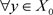 矛盾。所以,
矛盾。所以, 为一个KKM映象。
为一个KKM映象。
由Fan-KKM定理可知, ,s.t.,
,s.t.,

其次,证明 ,s.t.,
,s.t.,
 (3.2)
(3.2)
事实上,如果 ,i.e.,
,i.e.,

又因为
 ,
, 
根据(3.1)可知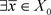 ,s.t.,
,s.t.,

也就是说
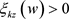 ,
, 
再由引理2.2可知

因此

最后,证明(SVEP)有解。
 , s.t.,
, s.t.,  ,
, 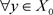
 i.e.,
i.e.,
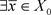 , s.t.
, s.t.
 ,
, 
定理3.1证闭。
注2:下面举例说明定理3.1是可行的。
例2:设 是一个集值映射,
是一个集值映射, 。F的定义如下:
。F的定义如下:

显然, 满足定理2.1中条件1、2。令
满足定理2.1中条件1、2。令 ,得
,得 ,经简单计算,显然
,经简单计算,显然 为解。
为解。
注3:在文献 [2] 中也讨论了类似的问题,但模型与文献中不同,下面举例说明。
例3:设 ,
,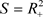 ,
, ,
, ,这里F的连续性和凸性可以保证。另外,
,这里F的连续性和凸性可以保证。另外, 。事实上,取
。事实上,取 ,
, ,
, ;i.e.,
;i.e., 为定理2.1的解。然而由简单计算可知,
为定理2.1的解。然而由简单计算可知, 。这样,对
。这样,对 ,x都不是文献 [2] 中模型的解。因此,定理3.1与文献中相应的结论是不同的。
,x都不是文献 [2] 中模型的解。因此,定理3.1与文献中相应的结论是不同的。
定理3.2 设 是X上的一个非空凸子集,
是X上的一个非空凸子集, 是一个集值映射,若满足下列条件:
是一个集值映射,若满足下列条件:
1) 对 ,
, 是X上的S-拟上半连续,
是X上的S-拟上半连续, 是S-拟下半连续;
是S-拟下半连续;
2) 对 ,
, 是
是 上的自然S-拟凸;
上的自然S-拟凸;
3) ;
;
则集向量均衡问题(SVEP)有解。
证明:设 ,首先我们证明
,首先我们证明 ,
,
s.t. (3.3)
(3.3)
构造集值映象
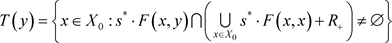 ,
, 
1) 对 ,都有
,都有 ,即
,即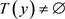 ,
, 。
。
2) 又因为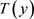 为一个紧集,
为一个紧集, ,且
,且 是紧的,故仅需证
是紧的,故仅需证 为闭集即可。
为闭集即可。
由T的定义可知
 ,
, 
再由F的连续性以及T的定义可得 为闭集。
为闭集。
3) 下面证明 为一个KKM映象。
为一个KKM映象。
因为具有 单调性,所以由Fan-KKM定理与定理3.1可知,(3.3)成立。
单调性,所以由Fan-KKM定理与定理3.1可知,(3.3)成立。
其次,我们证明 ,s.t.
,s.t.
 ,
, (3.4)
(3.4)
事实上,假设
 ,
,
即,

因此,由强凸分离定理可知,存在非零线性泛函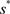 (
( ),s.t.
),s.t.
 ,
,  ,
, (3.5)
(3.5)
由(3.5)可知 ,
, 。又因为
。又因为 ,所以
,所以 。若不然,
。若不然, ,s.t.
,s.t. ,当
,当 ,
,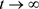 时,
时,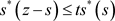 与矛盾。
与矛盾。
由(3.5)可知,取 得
得
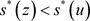 ,
, 
由(3.3)得。 ,
,
s.t. ,
, 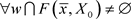
又因为 单调递增,所以
单调递增,所以

(3.4)得证。
下面类似于定理3.1中的证明。
定理3.2证闭。
致谢
笔者衷心感谢导师张宇副教授指导与帮助。
基金项目
国家自然科学资助项目(基金名称:集值极大极小问题与集值博弈问题研究,编号:11901511,主持人:张宇)。
参考文献
NOTES
*通讯作者。