1. 引言
2001年林华新教授因核C*-代数分类的需要 [1] 首次提出迹秩的概念。迹秩类似于拓扑空间的维数,是非交换代数的一种拓扑秩。它是C*-代数同构的不变量,在C*-代数分类研究中起着重要的作用。
广义迹秩是起源于S. Eilers,T. A. Loring和G. K. Pedersen定义一维非交换CW复形,林华新等人在此基础上定义了广义迹秩 [2],它是迹秩概念的推广,是C*-代数分类的又一重要不变量。本文研究了广义迹秩关于直和、商、遗传子代数以及归纳极限等的性质,并证明了
。
2. 预备知识
在此先列出本文用到的记号与定义。
设A是C*-代数。
(1) 记
是A中的正元集和投射集。
(2) 记
是A的单位化。
(3) 若存在一列投射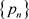 是A的近似单位,则称A是
-unital的。
是A的近似单位,则称A是
-unital的。
(4) 设
,定义函数
为
(5) 令
,若存部分等距
满足对任意的
,有
,
,其中
是a的值投影,且
,则记
。
设E是C*-代数A上的Hilbert C*-模。
(1) 对任意的
,对任意的
,定义
。
(2) 令
,称
中的元素为E上的紧算子。
(3) 令D为E的子集,如果D中元素的有限A-线性组合构成的子模在E中稠密,则称D是E的生成集。如果E有有限或可数生成集,则称E是可数生成的。
(4) 记
,则
是Hilbert A-模。
3. 主要结果
定义3.1. A是unital的C*-代数,若对于任意
,
,任意有限集
包含非零正元a,任意
,存在C*-子代数
以及投射
,
满足:
(1) 任给
,
;
(2) 任给
,
;
(3)
,
。
则称
。
当A是non-unital的C*-代数时,若
,则称
。
注3.2. 若X是有限维紧的Hausdorff空间则
亦为有限维空间,所以
,因此
。
定理3.3. 设
是unital C*-代数,若
,则
。
证明. 任意
,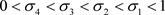 ,
以及任意有限集
,其中
,
以及任意有限集
,其中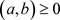 ,所以
。令
,
,则由
知对上述
,
分别存在
,
,所以
。令
,
,则由
知对上述
,
分别存在
,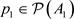 ,
, ,
满足:
,
满足:
(1) 任给
,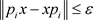 ;
;
(2) 任给
,
;
(3)
,
;
(4)
,
。
令
,下证
。
因为存在有限维代数
,
及同态
,
使得
及有限维代数
,
及同态
,
使得
。
令
,
则
,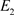 是有限维代数,
,
,是
,
从
到
的同态且
,则
是有限维代数,
,
,是
,
从
到
的同态且
,则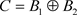 ,且
,所以
,且
,所以
(1) 任给
,
;
(2) 因为存在
,
使得
所以
所以
(任给
)。
(3)
综上得
。
□
注3.4. 设
是任意有限个C*-代数,若对于任意i,
,则
。特殊的,当A是unital C*-代数时,因为
,所以
当且仅当
。
定理3.5. 令A是unital C*-代数,若任意
,任意有限集
,存在unital C*-子代数
满足
且
,
,则
。
特殊的,对
,其中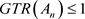 ,则
。
,则
。
证明. 任意
,
,
,任意有限集
,其中
。令
,则由 [3] 引理2.8知存在
,
满足引理2.8不妨设
,对于
由条件知存在unital C*-子代数
,
且
,所以对于任意i,存在
使
,存在
,使
。令
,则由
知对上述
,
以及
存在
,
,
,
满足:
(1) 任给
,
;
(2) 任给
,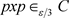 ;
;
(3)
,
,
所以
(1') 任意
,
(2') 因为对于任意的i,存在
使得
,则
同理因为存在
,满足
,所以
因此任给
,
。
因为
,所以
,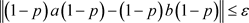 ,且因为
,
,且因为
,
所以由 [3] 引理2.8知
综上得
。
□
定义3.6. 设A是unital C*-代数,若对于任意
,
,任意有限集
包含非零正元a,存在C*-子代数
以及投射
,
满足:
(1) 任给
,
;
(2) 任给
,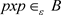 ;
;
(3)
,
则称
。
当A是non-unital的C*-代数时,若
则称
。
引理3.7. 设A为C*-代数,若
,则对任意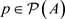 有
。
有
。
证明. 任意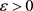 ,
,令
,
,
,令
,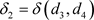 ,
,令
,
,
,令
,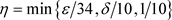 。
。
对于任意有限集
,且
,令
,对于上述
,
以及
由
知存在C*-子代数
,
,
,
满足:
(1) 任给
,
;
(2) 任给
,
;
(3)
,
由此得
同理 。
。
由 [4] 引理2.5.5知存在投射
,
满足
,
。由(2)知存在
,
,所以由 [4] 引理2.5.4知存在
,使
。则由 [4] 引理2.5.1知存在
满足
且
。
令
,则由 [3] 知
,且
满足:
(1') 任给
),
;
(2') 任给
),
;
(3')
,
所以 。
。
□
定理3.8. 设A是unital C*-代数,则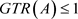 当且仅当
。
当且仅当
。
证明. 设
,则对于任意
,
,
,以及任意有限集
,其中
,则由
定义知当
时结论成立。下对n运用数学归纳法,假设
时结论成立,下证
时结论成立。
取
满足
,由则由 [3] 引理2.9知存在
,
,
满足引理2.9,令
,则由归纳假设知存在C*-子代数
,
,
满足:
(1) 任给
,
;
(2) 任给
,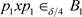 ;
;
(3)
,
。
由引理3.7只对于C*-代数
,有限集
存在C*-子代数
,
,
满足:
(1') 任给
,
;
(2') 任给
,
;
(3')
。
令
,
,则由定理1的证明知
,且
,经过简单的计算可知
(a) 任给
,
;
(b) 任给
,
;
(c)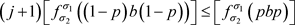 。
。
由(3')知
,又因为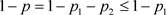 ,所以
,则由 [5] 定理3.3知
,所以
综上得
。
,所以
,则由 [5] 定理3.3知
,所以
综上得
。
□
附注3.9. 由引理3.7和定理3.8知若
,B是A的单位遗传子代数,则
。特殊的,对于A的单位理想I有
。
定理3.10. 设A是unital C*-代数,则
当且仅当任意
,
。
证明. 若
,由于
,所以由注3.9知
。
若
,则任意
,
,以及任意有限集
且存在
,
。设
是
的标准正交基,不妨认为
,取
满足
,设
以及任意取定
,令
,则存在C*-代数
,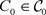 ,
,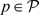 ,
,满足:
,
,满足:
(1) 任给
,
;
(2) 任给
,
;
(3)
。
由(3)知
。
令
,
,则
,且
(1') 任给
,
;
(2') 任给
,
;
(3')
,
。
令
,则由(3')知存在部分等距元
,满足
,
,又因为我们将
看做
,所以
是A的单位遗传子代数。令
,则由引理3.7知存在C*-子代数
,
以及投射
且
满足:
(1') 任给
,
;
(2') 任给
,
;
(3') 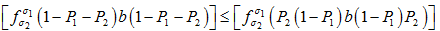 。
。
令
,易证
,
,当
足够小时,对上述
,有
(a) 任给
,
;
(b) 任给
,
;
(c)
。
综上可得
。
□
推论3.11. 设A是unital C*代数,
,则对于任意的AF-代数B,有
。
证明. 由定理3.10知对于任意n有
,又因为存在正整数列
使
是
的归纳极限,所以由定理3.5知
。
□
引理3.12. 设A是unital的C*-代数,D是在A中稠密的自伴子代数,若对于任意的
,任意的
,任意有限子集
,
,且
,存在非零投射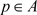 及A的C*-子代数
,且
,满足以下条件:
及A的C*-子代数
,且
,满足以下条件:
(1) 任给
,
;
(2) 任给
,
;
(3)
。
则
。
证明. 首先证明
。因为D是A的稠密自伴子代数,所以对于任给
存在
使得
。由
上的函数演算知
,即
,再用一次
上的函数演算可知
,且
,所以由
的任意性知
。
任给
,任意的有限集
,
,且
。取
使得
,由 [3] 引理2.8知,存在
,
满足引理2.8的条件,令
,不妨设
且
,由于
,所以对于上述
,分别存在
,使得
又因为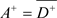 ,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件:
,所以存在
,使得
且
。令
,由于D满足题设条件,所以对于
及上述
存在A的C*-子代数
以及非零投射
满足下列条件:
(1) 任给
,
;
(2) 任给
,
;
(3)
。
所以对于任意的i,
(1')
.
(2') 因为对于任意的i,存在
,使
,
,所以
同理
。故
,任意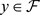 。
。
(3') 因为
,所以
,
。
因此由 [4] 引理2.8知
即
因此
。
引理3.13. 设A为unital C*-代数,
,
。设
,若存在
使得
,
,则
其中
,
。
证明. 因为
□
引理3.14. 设A为unital C*-代数,
,则 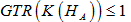 。
。
证明. 任意取定m,定义
上的投射
则
,所以
,因此可以将
看作是
的C*-子代数。
下面证明
。设I为
自身上的恒等算子,则
,且
为
的稠密自伴子代数。
对于任意
,
,取 满足
,由 [3] 引理2.8知存在
,
满足引理2.8的条件,不妨设
。
满足
,由 [3] 引理2.8知存在
,
满足引理2.8的条件,不妨设
。
任意有限集
。其中
,
,
,
,
,
,
。
不妨设
,
,
,
,
,则
,
,
,
在范数拓扑下收敛。
令
,
,
。
且对于任意
,对每个
分别存在
,
,
使得
当 时有,
时有,
令
设
则由引理3.13知
,
。
不妨设
,若不然因为
,则由
上的函数演算知
,由此得 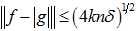 ,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。
,且因为
是
的C*-子代数知
,因此用
代替g即可。令
,则
为
的有限子集。
因为
有单位元,所以
,因此
,所以对
以及上述
,
,存在 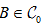 ,
,
,使
。
,
,
,使
。
满足:
(1) 任给
,
;
(2) 任给
,
;
(3)
。
则对任意
,任给
有
(1')
(2') 因为
,所以存在
使
,
。则
同理因为 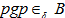 所以存在
使
,则
所以存在
使
,则
所以
,
。
(3') 因为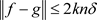 ,所以有
,所以有
所以由 [3] 引理2.8知
所以
由上述证明知
,
满足引理3.12的条件,所以可得
。
□
引理3.15. 设A是unital C*-代数,
,B是A的
-unital遗传C*-子代数则有
。
证明. 设
是B的一列近似单位,其中
。
对任意的
,有限集
,不妨设
,其中
。
选取
满足
,则由 [3] 引理2.8知存在
,
满足引理2.8的条件,不妨设
。
由于
是B的近似单位,所以对于 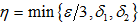 存在N使
存在N使
由B是A的遗传子代数易证
亦为A的unital遗传子代数。所以
。
对于
。由于
,所以对上述
,
,
存在
,
,
,
。
满足:
(1) 任给
,
;
(2) 任给
,
;
(3)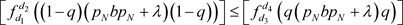 。
。
则
(1')
(2') 由(2)知对任给i,存在
使
则
(3') 由于
,所以
,所以
所以由 [3] 引理2.8知
所以
,即
。
□
定理3.16 设A为C*-代数,
,E是HAM。若
是
-unital的紧算子理想,则
。
证明. 因为
,且
,所以不妨设A是unital的。
因为
是
-unital的紧算子理想,所以E是可数生成的HAM。则由 [6] 定理15.4.6知
,所以
是
的遗传子代数。若
(1)
是unital紧算子理想,则由引理3.9以及定理3.14知
。
(2)
是
-unital的紧算子理想,则由引理
。