1. 引言
永磁同步电机是一种新型同步电机,因其高精度、高功率密度、高转矩惯性比、小体积等优越性能广泛应用于航空航天、船舶电力、电动汽车等领域,但许多学者在研究永磁同步电机时会忽略或近似波动因素(如忽略温度和阻尼影响、如空间磁场近似视为正弦分布等),讨论确定系统下的动力学行为,文献 [1] 在理想化条件下研究了车用永磁同步电机模型的抗扰和控制,其分析过程存在诸多限制,得不到更接近实际的结果;文献 [2] 在讨论永磁同步电机模型时指出了如磁链耦合等影响,并根据影响因素对系统进行了优化,但其优化是基于结构上进行的,并未对影响参数改进处理;文献 [3] 在确定的永磁同步电机模型下,引入了噪声干扰,但其动力学行为分析仍是基于规律性的正弦扰动。我们已知永磁同步电机工作时影响因素,电阻会受温度影响;摩擦系数会受阻尼影响;电感会受外部磁场影响。为了更好的提高永磁同步电机的鲁棒性需考虑上述影响参数,我们通过引入随机项对系统进行随机激励耗散的建立,便可获得一种更接近实际情况的描述思路。
目前,针对永磁同步电机模型,应用Hamilton理论进行分析的研究非常稀少,而随机动力系统的研究已有大量的理论方法,文献 [4] [5] [6] [7] 介绍了随机激励耗散Hamilton的知识,文献 [8] 介绍了调速器系统的随机分岔行为,这样便有机械系统引入随机噪声的参考可寻。本文在文献 [2] 的模型上引入了随机项,建立了随机参数激励下的永磁同步电机模型,首先运用中心流形定理对系统进行降维化简,再运用随机平均法得到Itô微分方程;接着讨论了系统稳定性并得出稳定性条件;最后进行分岔分析且选取合适的参数进行数值模拟。
2. 随机参数激励下的永磁同步电机模型建立
在交直轴电感近似相等的情形下,永磁同步电机基于同步旋转坐标下的数学模型 [2] 表示如下:
(1)
系统变量及参数的物理意义:
为d-q轴定子电流,
为d-q轴定子电压,w为转子机械角速度,R为定子电阻,L为定子电感,
为负载转矩,J为转动惯量,B为粘滞摩擦系数,P为极对数,
为转子磁链,所涉及参数均为正数,求得非负平衡点为:
。
考虑系统(1)中参数电阻R,电感L,摩擦系数B,转子磁链
会受内部温度外部磁场、阻尼、耦合等因素影响变得不稳定,把影响因素视为白噪声,对其引入随机项:
,得到一个新的随机非线性微分方程:
(2)
其中
为白噪声强度,
为零均值白噪声,其中
接着令
,系统(2)可化为:
(3)
其中:
3. 永磁同步电机模型的处理
据上述推导关系知,系统(3)在
处的性质等价系统(2)在平衡点
的性质,我们可把系统(2)在
的稳定性转化为系统(3)在
处的来讨论。模型(3)的特征方程为:
(4)
其中:
求得方程(4)的特征值为:
,
令
,
,当参数
趋近于零时,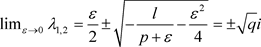 ,
此时点
将退化为系统(3)的临界焦点,具有局部不变流行的性质。
,
此时点
将退化为系统(3)的临界焦点,具有局部不变流行的性质。
令
与
的关系式如下:
则系统(3)可变为:
(5)
其中:
此时系统(3)在原点附近具有局部不变流行:
对系统(5)降维可近似表示为下式:
(6)
其中:
且h满足
的全微分
,所以将
的全微分代入(6)式得,
我们要求解的中心流形可用下式来逼近:
代入上述方程两边相同幂系数合并得:
忽略高阶项,可进一步得到系统(7)
(7)
令
,进行极坐标变换系统(7)可转化为:
(8)
其中:
在解决系统(8)时,精确解不易求出,但可基于Khasminskii极限定理 [4] [9] [10] [11],当白噪声强度充分小时,其反应
弱收敛于一个二维的马尔可夫扩散过程,运用随机平均法,系统(8)可得到Itô随机微分方程:
(9)
对于上述二维马尔可夫扩散过程,计算它的转换概率密度,方程(9)表达为:
(10)
其中:
根据扩散矩阵,可以得到平均振幅是一维的马尔可夫过程,如下式(11):
(11)
这样,在讨论模型的稳定性和随机分岔时获得一个思路,即根据参数的随机概率密度分布,分析在概率密度意义下平均振幅的稳定性和临界分岔。
4. 稳定性分析
4.1. 局部稳定性
讨论局部稳定时,基于Oseledec乘性遍历理论 [4] 和最大Lyapunov指数法,随机方程平凡解在概率意义下稳定的充要条件为:最大Lyapunov指数
。
我们讨论线性Itô随机微分方程的稳定性,首先令
,即讨论
时方程(11)的稳定性,此时方程变为:
(12)
对微分方程(12)求解得,
其中
,
根据拟不可积Hamilton系统理论 [5],线性Itô随机微分方程的Lyapunov指数近似表示为:
。
这样可得方程(12)的Lyapunov指数:
① 当
,即
时,线性Itô随机微分方程(11)是局部稳定的,即原系统(2)在平衡点处是稳定的;
② 当
,即
时,线性Itô随机微分方程(11)是局部不稳定的,即原系统(2)在平衡点处是不稳定的。
4.2. 全局稳定性
在分析局部稳定性时,应用Oseledec乘性遍历理论和最大Lyapunov指数判定方法,但该理论方法只适用于做局部稳定性判断,接下来分析全局稳定性,我们可用奇异边界理论 [4] [5] 对其全局稳定性做分析判断。
首先介绍奇异边界理论,我们已知r,此外还有扩散指数
;漂移指数
;特征指数
。
I) 如果有
,即
,系统为第一类奇异边界,第一类边界下:
当
时,
是排斥自然边界,
是吸引自然边界,
是严格自然边界;
II) 如果有
,即
,系统为第二类奇异边界,第二类边界下:
当
,
时,
是排斥自然边界,
是吸引自然边界,
且
是严格自然边界;
当
时,
是进入边界。
上述为奇异边界理论介绍,接下来我们分两种情形进行分析,即
情形。
1) 当
时,系统如上述(12),
时系统(12)为第一类奇异边界,经过计算可以得,
,
,
,则有:
是排斥自然边界,
是吸引自然边界,
是严格自然边界;
时系统(12)为第二类奇异边界,经过计算可以得,
,
,
则有,
是排斥自然边界,
是吸引自然边界,
是严格自然边界。
综上可得出结论:
① 当
,
为吸引自然边界,
是排斥自然边界,则Itô微分方程(11)有概率意义下稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是稳定的;
② 当
,
为排斥自然边界,
是吸引自然边界,则Itô微分方程(11)有概率意义下不稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是不稳定的;
③ 当
,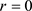 和
为严格自然边界。
和
为严格自然边界。
2) 当
时,系统为方程(11),
系统(11)是第一类奇异边界,经过计算可得到,
,
,
,则有:
是排斥自然边界,
是吸引自然边界,
是严格自然边界;
系统(11)为第二类奇异边界,经计算
,
,则
是二类奇异边界中的进入边界。
综上可以得出结论:
① 当
,
是吸引自然边界,且
是进入边界,则Itô微分方程(11)有概率意义下稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是稳定的;
② 当
,
时为排斥自然边界,而
是进入自然边界,则Itô微分方程(11)有概率意义下不稳定的平凡解,说明系统(2)在白噪声激励下平衡点处是不稳定的;
③ 当
,
时为严格自然边界。
5. 随机分岔分析
随机分岔理论 [4] [5] 是通过研究参数的变化,对随机动态系统进行性态分析,我们将应用拟不可积Hamilton系统随机平均法来解决随机分岔动力学行为。
5.1. 随机D-分岔分析
当Itô随机微分方程(11)中
时,方程即为:
(13)
由于
方程变为不发生分岔的确定系统,我们讨论
时的情形,令
,
,方程(13)生成的连续动态系统为:
(14)
式(14)为方程(13)以x为初值的唯一强解。当
时,0是
的固定点,对此固定点,
是Stratonovich的随机意义下的激参,设
有界,则对
满足椭圆性条件的
,保证最多有一个平稳概率,则对应的FPK方程为:
(15)
其中,令
得到与方程(15)相应的平稳概率密度:
(16)
这样,则该动态系统可能有不动点、非平凡平稳两种平稳状态,且二者不变测度
和
的密度分别为
和(16)式,此时还需确定两不变测度的Lyapunov指数,解线性Itô随机微分方程(13)为:
(17)
已知系统测度的Lyapunov指数:
(18)
根据公式
得,不动点状态的Lyapunov指数:
(19)
设
有界,
可积,将式(17)代入方程(18),非平凡平稳状态的Lyapunov指数为:
(20)
令
,则根据二者不变测度的Lyapunov指数可判定,当
时前者不变测度稳定,当
时后者不变测度稳定,即系统(2)的一个D-分岔在
处发生。
我们进一步处理系统(16)可以得到:
(21)
其中:c为归一化常数,
,当
,即
时,
是一个
函数,当
,即
时,
是
在该区间的最大值点,所以随机系统(2)发生D-分岔的临界条件为,
,即
。
当Itô随机微分方程(11)中
时,令
,
,则方程(11)变为:
(22)
当
时,系统为确定分岔-叉形分岔,当
时,讨论
时,有唯一密度为
不变测度
;
时,动态系统的平衡状态相应的不变测度分别为
和非平凡平稳状态测度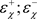 ,密度为:
,密度为:
(23)
(24)
其中
,则根据式(19)得
的Lyapunov指数为:
(25)
根据方程(20),(23),(25)可得两个非平凡平稳状态测度
的Lyapunov指数为:
(26)
所以
时,随机系统(2)的发生D-分岔。
5.2. 随机P-分岔分析
令
,
,则方程(11)变为:
(27)
可得到方程(27)的FKP方程为:
(28)
其初值条件为:
,
,
,
为扩散过程的转移概率密度,
的不变测度是平稳概率密度,若令
,则退化系统的解为:
对系统进行P-分岔分析时,我们的思路是由线性Itô随机微分方程的概率密度
计算不变测度极值,进而分析分岔。根据Namachivay’s理论 [4] [10] [12],当噪声
趋于0时,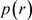 的极值趋表现稳态特征,当系统响应
是遍历的,由乘积遍历性定理得
是样本轨线在 的邻域内访问时间的度量。
的极值趋表现稳态特征,当系统响应
是遍历的,由乘积遍历性定理得
是样本轨线在 的邻域内访问时间的度量。
若
在
处为极大值,轨线在
的邻域内停留时间较长,说明
在概率意义下是稳定点;若
在
处为极小值,轨线在
的邻域内停留时间较短,说明
在概率意义下是不稳定点。
6. 数值模拟
综上可知原系统的响应过程为
,且
,所以我们主要分析
的联合概率密度
即可,在实际意义下,赋值参数
,使得
,在此情况
下,给出平稳概率密度函数和联合概率密度函数模拟图像。
若设
,图1中左图表示,取不同的负值
,平稳概率密度函数是单调递减函数,且随
的增大图像减势变弱,右图表示
时联合概率密度图像呈现单峰尖状;图2中左图表示在
附近,随
值增大平稳概率密度函数从递减变为有极值状态,右图表示
时联合概率密度图像呈现单峰状,说明此时并未发生分岔;图3中左图表示,取不同的正值
,平稳概率密度函数是极值函数,且随
的增大平稳概率密度函数极值峰谷趋于平缓,右图表示
时联合概率密度函数呈现火山口形状,则系统在临界点
后发生了分岔。

Figure 1. The left figure shows stationary probability density function image of
; The right figure shows joint probability density function image of
图1. 左图表示
分取−0.22,−0.12,−0.02时平稳概率密度函数图像;右图表示
联合概率密度函数图像
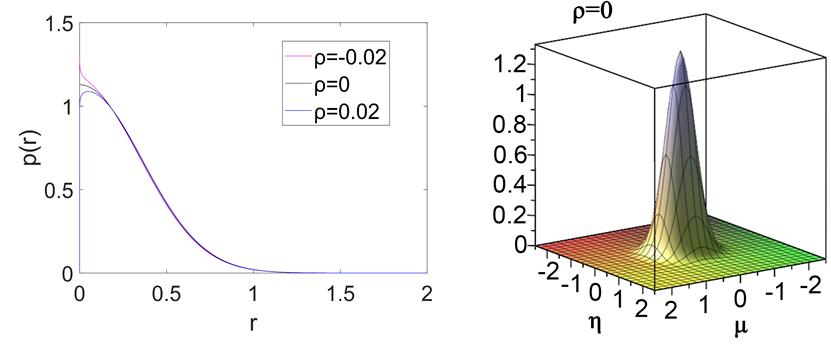
Figure 2. The left figure shows stationary probability density function image of
; The right figure shows joint probability density function image of
图2. 左图表示
分取−0.02,0,0.02时平稳概率密度函数图像;右图表示
联合概率密度函数图像
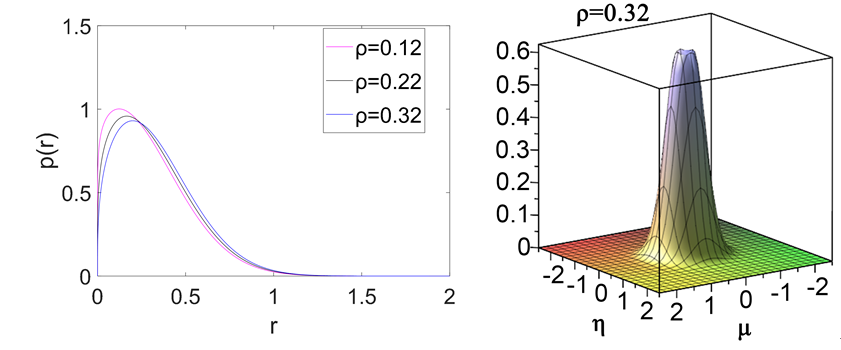
Figure 3. The left figure shows stationary probability density function image of
; The right figure shows joint probability density function image of
图3. 左图表示
分取0.12,0.22,0.32时平稳概率密度函数图像;右图表示
联合概率密度函数图像
7. 结论
本文讨论了在随机参数激励下永磁同步电机的稳定性和分岔,把随机参数视为白噪声,运用随机激耗散的Hamilton理论,对系统的动力学行为进行分析,结合实际意义选取分岔参数
,根据数值模拟结果得出当
时系统发生分岔行为,说明此时永磁同步电机系统有可能会变得不稳定。