1. 引言
三支决策(3WD)是Yao [1] 在2009年提出。由于三支决策思想是一种符合人类认知和思维模式的处理问题的方式,一经提出就在医学、工程、管理、信息等领域得到了广泛的应用 [2] [3] [4]。 近几年来在与粒计算结合处理多粒度信息系统中不同粒度下的信息方面,受到国内外学者的广泛关注,并取得一些重要成果 [5] [6]。 将三支决策的思想与文本分析相结合,能够在信息不足或者描述不明确的情况下,将有争议的部分延迟处理,有效避免了二支决策中由于信息不足引起的盲目决策问题。三支决策的最初的思想就是将整体分为三部分,不同的部分采取不同的处理方法。目前仍有一些研究人员认为这三部分必须相互独立,现在Yao [7] [8] 提出了一种新的Three-way decision+ (3WD+)模型,发现三部分之间存在着内在联系,并不完全独立,三个部分之间可以有交叉,在一定条件下甚至可以相互转化。这个扩展极大促进了三支决策的发展。
1965年Zaded [9] 的文章标志着模糊数学的诞生。随着计算机的快速发展,需要处理的数据规模越来越大。一些学者将模糊数学与粒计算、三支决策等理论结合,并取得一些成果。比如折延宏等 [10] 在多粒度决策信息系统中采用三支的方法,将多粒度决策系统的信息分层,然后讨论粒度协调性,以解决对象更新的问题;魏玲等 [11] 将三支决策与粒计算、形式概念分析结合,提出三支概念分析理论,并得到成功的应用。毛华等 [12] [13] 在三支概念基础上,提出一种新的概念格的分类,并研究了模糊概念格表达与测量,取得一些成果。
在一个多粒度信息系统中,不同粒度下的评价标准在很多时候并不相同,那么单个粒度中的形式背景必然不同。形式背景中属性值通常有数值型、区间型、文本型等。同类型的评价标准仅仅需要消除量纲的影响就可相互转化,如区间转区间、数值转数值这些都是相对容易的,相关方法也比较多。但是区间转数值、文本转数值等不同类型的评价标准之间的转换不仅涉及量纲,因此难度大大提升。尤其是相对于数值和区间型数据,文本型数据还具有主观性,因此,在转化为数值或区间形式时的难点会更多。同时,文本型数据又是生产、适合以及科研中最常见的一种数据形式之一,所以,文本值的数值化很有研究价值。
虽然关于数值型形式背景分类、统一化归的方法,现已有不少成果 [14] [15] [16]。 但是关于文本型的形式背景数值化方法,目前的研究成果相对较少,影响了含有文本型形式背景的应用与发展。为了解决这一问题,本文提供一种方法,既可以用于文本型形式背景详细地划分,从而得到一种数值化的结果,也可以用于在一个多粒度信息系统中,对于不同粒度,由于标度不同而导致的数值型和文本型等不同类型的形式背景,可以通过化归到同一度量标准的方法来处理这些不同类型的度量标准的情况。
然而在实际应用中,更多地会遇到无法准确判定的情况。比如在网络购物的评价过程中,在对关键词抓取之后,对于评价的系统评分的这个过程,就是文本的数值化过程。不同的用户的评判标准是不同的,所以,在此文本型数据的数值化过程就需要选择一个合适的阈值。本文结合三支与模糊数学的隶属度原则,将多粒度信息系统中出现的文本型粒度提取出来,然后通过语言标度分割和不同的阈值的选取,将原本分割后形成的三部分进一步地划分,从而达到符合用户需求的情况。本文提出的三支模型,无论是在适用性上,还是在应用范围上,都比传统的语言标度分割方法更具优势,在划分上也会更加精确。
2. 基础知识
本节将本文所需要用到的定义依次地介绍。
首先,需要介绍形式背景和对象与属性之间的关系。
定义2.1 [11] 形式背景K是一个三元组
,其中K为所有对象的集合,M为所有属性的集合,
为G和M中元素之间的关系集合。对于
,
记为gIm,表示“对象g拥有属性m”。
对象的属性通常有一个统一的度量标准,但是在多粒度信息系统中,不同的粒度度量标准有所差异。属性值的表示形式通常有数值
,区间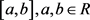 ,以及文本w,w为文字语言,本文中将所有的数值数据和区间数据统称为数值型数据,非数值型数据称为文本型数据。尤其是涉及到文本型数据的度量的时候,应当将文本型转化为更容易量化的数值型。
,以及文本w,w为文字语言,本文中将所有的数值数据和区间数据统称为数值型数据,非数值型数据称为文本型数据。尤其是涉及到文本型数据的度量的时候,应当将文本型转化为更容易量化的数值型。
定义2.2 [11] 一个文本型形式背景
。其中G是对象集,M是属性集,
是文本型属性值的集合,
是它们之间的一个三元关系,定义为:
,当且仅当 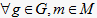 有且仅有一个文本值
满足
有且仅有一个文本值
满足 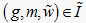 。
。
对于不同类型的形式背景,通常有不同的处理方法。对文本型形式背景,如何把文本值转化为数值或者区间,就需要用到三角模糊函数和语言标度分割原理。其中在文本值转化为三角模糊函数中,迫切需要定义左边NEG和右边POS的起始域的边界值分别记为
,这将在下面的定义中完成。
定义2.3 [11] 将对象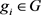 在属性
下的属性值记为
,
。属性值
所对应的状态集合记为
。当属性值
时属于N即NEG;当属性值
在属性
下的属性值记为
,
。属性值
所对应的状态集合记为
。当属性值
时属于N即NEG;当属性值 时属于P,即POS,中间状态属于B即BET。
时属于P,即POS,中间状态属于B即BET。
其次,在将转化文本值的过程中,还需充分了解隶属度方面的知识。
定义2.4 [9] 给出映射
,
,则称
确定一个X的模糊子集
。
称为
的隶属函数,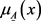 称为x对
的隶属度。
称为x对
的隶属度。
隶属函数,是用于表征模糊集合的数学工具。为了描述元素u对U上的一个模糊集合的隶属关系,由于这种关系的不分明性,它将用从区间[0,1]中所取的数值代替0,1这两值来描述,表示元素属于某模糊集合的“真实程度”。
定义2.5 [9] 给定一个论域U,那么U到单位区间[0,1]的一个映射
称为U上的一个模糊集,或U的一个模糊子集。
模糊集合这一概念的出现使得数学的思维和方法可以用于处理模糊性现象,从而构成了模糊集合论,即模糊数学的基础。
为了将文本值表示成为数值形式,引入三角模糊数的定义如下:
定义2.6 [9] 所谓给定论域U上的一个模糊集,是指对任何
,都有一个数
与之对应,
称为x对U的隶属度,μ称为x的隶属函数。
设s和u分别为模糊数的下限和上限,m为可能性最大的值,那么模糊数用
表示。
关于阈值及最大隶属度的相关定义如下:
定义2.7 [9] 设
,对任意
,记
称 为
的
-截集,
为
的
-截集, 称为置信水平。又记
,称
为
的
-强截集。
称为置信水平。又记
,称
为
的
-强截集。
定义2.8 [9] 最大隶属度原则:设
为n个标准模型,
,如果存在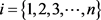 ,使得隶属度
,则称
相对隶属于
。
,使得隶属度
,则称
相对隶属于
。
3. 新的文本型形式背景转换模型
对于含有文本属性值的形式背景,本节将给出一种文本值数值化的新模型。该模型采用三支决策思想与模糊数学相结合的方式,选取不同的阈值反复地进行循环,最终得到符合用户要求的三部分。
3.1. 定义
当在一个多粒度信息系统中遇到语言描述的属性值时,通常采用三角模糊函数依语言标度分割后,一个对象同时属于一个属性下的一到两栏,这样就造成非此即彼的情况。实际情况中,文本描述是比较模糊的,有些无法用数值准确地界定。基于文献 [9] 中给出的三角模糊函数最后得到的每个对象最多隶属于两栏中,而改进后的三角模糊函数的复合函数定义如下:
定义3.1 设存在四个三角模糊数
,
,
,
。任给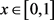 ,分别对应的隶属度如下
,分别对应的隶属度如下
则称为复合函数。
此处,1)
=“C标准的最右边的点”;2)
=“B标准的中点”;3)
=“A标准的最左边的点”;4)
。
从定义3.1中可以看出,同一事件在一个评价标准下,会有三种不同的评价,假设这三种评价为A,B,C。例如,在学生考试评价体系中,A为优秀,B为及格,C为不及格。
3.2. 模型建立的思想
首先,对文本型数据描述的属性值,用三角模糊数依次表示为数值形式,得到一个对应于原形式背景的数值形式背景。
其次,在此数值形式背景下,利用改进后的三角模糊函数,对此文本值进行处理,得到一个对应于此形式背景中的属性值之几何坐标表示。其中横坐标表示:所有三角模糊数所在的[0,1]区间;纵坐标表示:三角模糊数区间上的点在相应的文本值的隶属度。
最后,在上面得到的几何坐标表示下,对于横坐标从左向右依次完成如下工作:
1) 从左到右第一个隶属度为1的点的横坐标记为a,直至到一个隶属度为1的点的横坐标记为b。 ,
,
。
,
,
。
2) 在此几何表示中利用阈值和隶属度,并结合三支决策的思想,将横坐标的[0,1]区间分为三部分,记为
之后,在此三部分上讨论提供原形式背景的用户对背景内容划分的界定要求,达到用户对原形式背景中全体对象进行综合评价的要求。
以上从“首先”至“最后”所有步骤,实际上是复合函数的代数计算过程,通过这些步骤可得到一个基于用户需求的数值显示背景的三支划分。
三支决策中,通常划分的三部分,可以每部分都有对象,也可以其中某一部分为空。例如,如果顾客对某一项的评价全部为满意,那么差的那部分就为空。故在用模糊函数对文本型形式背景进行划分的时候,不必拘泥于三部分一定要含有相应的区间或元。当三支的其中一部分是空集的时候,可在下一步划分的时候,将其他部分划过去,也可将其看作三支的一个特殊情况。
3.3. 模型实现的算法过程
对于文本型形式背景三角模糊数的复合函数的算法如下:
算法1 基于
的三支划分
输入:文本值
,三角模糊函数
,阈值
,对象
,属性
,
,
;
输出:
;
Step0:初始化
,
;
Step1:将文本值表示成三角模糊数的形式:
,
,
,
,其中
,
,
;
Step2:开始计算符合函数中各点的坐标,将文本值在三角模糊函数上的第一个隶属度为1的点的横坐标记为a,最后一个隶属度为1的点的横坐标记为b,即分别是
和
,则
,
,
;
Step3:记
与
的交点为
,
与
的交点为
;记
与三角模糊函数上的在点
的左右两边的交点横坐标记为
和
;在点
的左右两边的交点的横坐标记为
和
;
Step3.1:当
时,
;在左边
,隶属度
,则
;
中,因
,故
。右边,
中,有
,故
;
中,因
,故
。
故
时,
,
,
;
Step3.2:当
时,
;在左边
,隶属度
,则
,故
。右边
中,
,故
。
故
时, 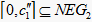 ,
,
;
,
,
;
Step3.3:当
时,
;在左边
,中隶属度
,故 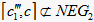 ;右边
,中隶属度
,故
;右边
,中隶属度
,故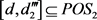 ;在
中,隶属度
,故
。
;在
中,隶属度
,故
。
故
时, 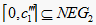 ,
,
;
,
,
;
Step3.4:当
时, 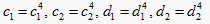 ;在左边
,中隶属度
,故
;在
中,隶属度
,故
;左边
中,隶属度
;在左边
,中隶属度
,故
;在
中,隶属度
,故
;左边
中,隶属度 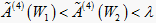 ,故
。
,故
。
故 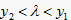 时,
,
,
;
时,
,
,
;
Step4:当
时,
;否则转Step5;
Step5:当
时,
;否则转Step6;
Step6:输出 。
。
算法2 最优三支划分算法
输入:阈值
,其中
,
, 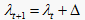 ,
和
其中
;
,
和
其中
;
输出: NEG,BET,POS;
Step0:初始化当
;
Step1:调取算法1;
Step2:当
或者
时,算法结束;否则
,转Step2;
Step3:输出
。
注:
选取的是含于算法1中所得到的
,选取的方式是按用户对NEG这一部分的需求。
在划分过程中,用户可得到
三部分。实际上,这三部分是由用户对其中一部分限定了范围而得到的。
比如用户需要“优秀”、“合格”和“不合格”三部分,但是对其中某一部分的范围有所要求。对于不同的要求都可以用上述算法得到。
当对“优秀”这部分要求的范围为0.3时,可以将算法2中的
替换成为
,并且
,即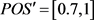 。选取不同的阈值
,对算法1中的
,再次划分直至得到符合用户需求的最佳划分。当对POS的要求不同时,选取的阈值也不同,则最后出来的三部分自然不同。
。选取不同的阈值
,对算法1中的
,再次划分直至得到符合用户需求的最佳划分。当对POS的要求不同时,选取的阈值也不同,则最后出来的三部分自然不同。
当用户需要得到中间部分即“合格”这部分时,同样可以用以上算法,将
替换为
通过选取不同的阈值得到符合需求的最佳划分。
3.4. 算法分析
当用户需要得到中间部分即“合格”这部分时,同样可以用以上算法,将
替换为
通过选取不同的阈值得到符合需求的最佳划分。本节分三部分完成:一是算法的正确性、二是算法的复杂度分析、三是与已有成果的比较。
3.4.1. 算法的正确性
算法主要思想是,通过取不同的阈值对得到的三部分,不停地进行收缩或者放大以便达到用户需要。下面分别对算法1和算法2加以分析。
算法1 是将文本值用三角模糊数表示出来,然后对三角模糊数进行初步的分层得到
,
和
。然后选取一个阈值
再次进行分层。根据
取值不同分别对应四种不同的处理方式,在对应的情况下依据隶属度原则再次进行分层。所以算法1在有限步内可以结束。
定理3.1 当给出一个初始阈值
对已知三角模糊数属性值分层,一定存在一个梯度
可以在有限步内使
或者
。
定理3.1是对算法2的总结。要说明算法2能在有限步内结束,即证明定理3.1的正确性。
证明:当
时,对应的是算法1中的第一种情况,此时输出的 。在算法2中
。在算法2中
阈值
取值逐步上升,当
取值在
,
中间时,对应的算法1中的第三、四情况,此时依据算法NEG的区间会逐渐减小,直至
取值增至大于 和
和 ,此时NEG区间仍然在缩小。故随着阈值的逐渐增大,NEG的区间逐渐在减小,由于算法2中的限定条件为
或者
,故最后一定存在一个满意阈值
(该阈值为所有满足要求的最大阈值)使
,或者存在一个满意阈值
(该阈值为所有满足要求的最小阈值)使
。当
的第一个取值较大进行缩小时,同上理可以得到一个满意阈值,将文本值划分为需要的三部分。
,此时NEG区间仍然在缩小。故随着阈值的逐渐增大,NEG的区间逐渐在减小,由于算法2中的限定条件为
或者
,故最后一定存在一个满意阈值
(该阈值为所有满足要求的最大阈值)使
,或者存在一个满意阈值
(该阈值为所有满足要求的最小阈值)使
。当
的第一个取值较大进行缩小时,同上理可以得到一个满意阈值,将文本值划分为需要的三部分。
之后,算法2根据对NEG,BET或者POS的输出要求,选择对
梯度放大或者缩小,再次调用算法1直至得到符合最终要求的三部分。
3.4.2. 算法的分析
第二,算法的复杂度分析:
在算法的正确性分析可知,算法1的复杂度为
,算法2的复杂度为:
,其中
。
故算法整体的复杂度为
。
第三,与已有成果的比较:
在多粒度信息系统中,处理文本值的常用方法实际上是一个二支划分的过程。而本文将三支决策的方法引入文本值数值化的划分中。与二支方法相比,上述算法模型主要有以下突出优势:
通过三支的思想,解决了传统方法在文本值数值化过程中,直接将区间一分为二的做法。从隶属
度的角度,将区间分为三部分,得到一种更符合实际情况的划分。并建立一个复合函数,将三角模糊数表示的文本值用几何形式直观的表示出来。通过阈值的变化,能过扩大或者缩小划分出的某一区间,能够根据需求,灵活的选择不同的阈值,从而扩大应用范围。
3.5. 实例
下面给出一个实例说明算法的实际操作步骤。
例1:在某购物网站的售后评价体系中顾客可分别对物流服务
、货物质量
、卖家态度
、售后服务
四项评价,四项评价档次分别有“满意、一般、待改进、较差”,顾客可根据实际情况对此次购物体验做出相应的评价。评价提交后平台的系统会对此商品做出一个整体的评价,但平台出于长效发展的考虑,在整体的服务质量都不高的情况下,可将评价标准降低,即扩大POS这部分的范围或者缩小NEG的范围;当平台出于可持续发展的考虑应该使BET的部分在NEG,BET和POS三部分占比最大。故用户(即此例中的购物平台)可以根据自身的需要调整阈值将评价分为三部分。
下面为某平台提供的近几位购买某一产品的顾客的评价结果,如表1。
从表1中可以看出,评价为“一般”和“满意”的较多。为了提高平台的货物质量
,在将其区间化的过程中可适当扩大NEG部分的范围,以达到促进发展的目的。
第一步,将文本值转化为相应的三角模糊数:W = {较差,一般,待改进,满意}。其中:“较差”= W1 = (0,0.2,0.4),“待改进”= W2 = (0.3,0.5,0.7),“一般”= W3 = (0.4,0.6,0.8),“满意”= W4 = (0.6,0.8,1)。
根据模糊数的定义将文本型背景转化为数值型(见表2)。
第二步,根据语言标度分割原理和给定的三角模糊数,可以得出如图1的三角模糊数的图示。对于
区间内,在横坐标轴上,从左向右,令
。得到
确定点
,其中
;
令
,得到
。
确定点
,其中 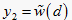 。且
。
。且
。
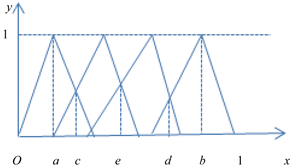
Figure 1. Collective representation of attribute values in Table 2
图1. 表2中属性值的集合表示
另外,
。
从图1中可以看出,改进后的三角模糊函数使一个对象可以同时归结到一个属性下的一到三栏中甚至四栏中。可根据语言标度分割原理,将三角模糊函数的图画出来,当它在某一栏的隶属度明显高于其他栏的时候,如果在图的左边则记为NEG,如果在图右边则记为POS;当同时属于两栏或三栏时,记为BET,然后对BET这一部分进行分析细化,再根据实际情况给出合理的划分。
第三步,在图1中,将第一个拐点的横坐标记为a,最后一个拐点的横坐标记为b,函数图像的第一个交点的横坐标记为c,纵坐标记为
,
“一般”和
“待改进”,三角模糊函数的交点为横坐标记为e;将最后一个交点的横坐标记为d,纵坐标记为
。由函数图像可明显地看出,当
时,该区间在“较差”这一属性下的隶属度明显高于其他,故可记
;同理可记
.而a与b之间的部分可暂记为BET,即
。
第四步,根据实际情况,需要给出一个阈值
。
当
取值较小,即
时,如图2所示。
记
,在三角模糊函数图像除
区间上的第一个交点的横坐标记为
。显然在左边
中,在
这一三角模糊函数上的值明显比
上的值隶属度要大的多,故
;在右边,记
,在三角函数图像除 区间上的最后一个交点的横坐标记为d,同理
。
区间上的最后一个交点的横坐标记为d,同理
。
综上,当
时,
,
,
。
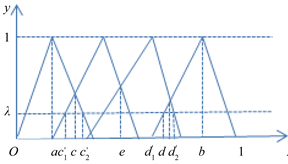
Figure 2. Graphical of triangular fuzzy number when threshold is small
图2. 阈值较小时三角模糊数图示
当
取值较大时,即 时,如图3所示。
时,如图3所示。
记
,在三角模糊函数图像除
区间上的第一个交点的横坐标记为
,与除
外的最后一个交点的横坐标记为
。在左边,显然函数在
区间上的取值大于
,故可将
并入NEG中;在右边,同理将
并入POS中。至于中间的
和
这两部分,暂时还放在BET中。
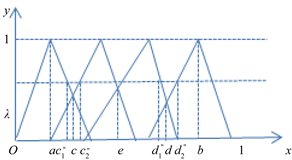
Figure 3. Graphical of triangular fuzzy number when threshold is big
图3. 阈值较大时三角模糊数图示
综上,当
时, 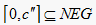 ,
,
。
,
,
。
当
时,此时又分为两种情况
和
,分别如下图4和图5所示:
同上记
,与三角模糊函数图像的交点的横坐标分别为
(除
区间上的第一个交点的横坐标)和
(除
外的最后一个交点的横坐标)。
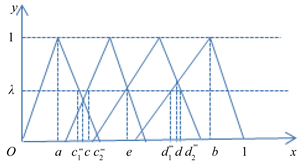
Figure 4. Graphical of triangular fuzzy number (
)
图4. 三角模糊数图示 (
)

Figure 5. Graphical of triangular fuzzy number (
)
图5. 三角模糊数图示(
)
当
即
时,由图4可以看出,在
中时,
在三角模糊函数上的隶属度大于在
上的隶属度,故
。在右边,
中,显然
在三角模糊函数上的隶属度大于
,将
与
的另一个交点记为
,当
时,虽然隶属度上
比
小,但是在
的隶属度大于
,所以仍然有
。
综上,当
时,
,
,
。
当
,即
时,由图5可以看出,在 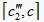 中,
在三角模糊函数上的隶属度大于在
上的隶属度,必然有
;将
与
的另一个交点的横坐标记为
,在
中,虽然
在三角模糊函数上的隶属度小于在
上的隶属度,但是大于
,所以
。在右边同图4的分析可知
。
中,
在三角模糊函数上的隶属度大于在
上的隶属度,必然有
;将
与
的另一个交点的横坐标记为
,在
中,虽然
在三角模糊函数上的隶属度小于在
上的隶属度,但是大于
,所以
。在右边同图4的分析可知
。
综上可得,当
时,
,
,
。
第五步,选取新的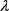 重复第四步,直至
停止;
重复第四步,直至
停止;
第六步,得到最终的
,
,
。
上述步骤是将所有文本型属性值转化为用三角模糊函数表述的区间形式,然后对属性
中区间型属性值的三支划分。可以容易地看出,此形式背景中
,
,此计算中选取了一个阈值
,以及
的情况,故
,故此处的算法复杂度为
。
4. 结语
当一个多粒度信息系统中存在不同的度量标准时,为了方便决策,需要将所有的属性值转化在一个统一的度量标准下。而文本型数据的度量标准一直是量纲统一化的重点和难点,本文提出的这种方法可以用于文本型数据在数值化过程中的取值困难的问题。本文用三角模糊函数表示文本值,并定义了一个三角模糊数的复合函数,使得文本值从简单的模糊区间形式转化为直观的几何形式。从几何表示中可以看出,文本值在区间上的每个点对应的隶属度,继而利用阈值与三支决策的思想,将文本值对应的区间进行放大或缩小,最后得到用户所需的划分结果。
本文采用三支决策的思想,避免了与传统的语言标度划分方法在划分过于绝对的弊端。用三角模糊数表示文本值为后续区间的缩放提供了方便,定义的复合函数将区间形式的文本值表示转化成了几何形式,这种表现方式更加的直观。并且本文提供的模型,能够使用户根据需要合理的变换阈值,以得到所需结果。这种文本型形式背景的数值转化方法,在当今互联网的迅猛发展和企业管理员工评价机制上具有实际且广泛的应用。
由于本文处理的文本值的个数为4个,这是最常见的情况。但当文本值个数大于4个时,仍有很大的研究价值,需进一步探讨。
基金项目
基金项目:国家自然科学基金(No.61572011)、河北省自然科学基金(No.A2018201117)、河北大学研究生创新资助项目(No.hbu2019ss030)。
NOTES
*通讯作者。