1. 引言
设X是Banach空间。考虑X中带非局部积分边界条件的非线性分数阶发展方程
(1)
的精确可控性。其中
,
是常数,
是
阶Caputo型分数阶导数;
是X中一致有界的等度连续半群
的无穷小生成元,即
,使得对
,有
,控制函数
,U是Hilbert空间,
线性有界算子;
是给定的函数;
是非局部函数
,定义如下:
,
其中
是一个给定的函数。
1993年,Leela等 [1] 在A生成紧算子半群时,研究了具有固定脉冲的控制系统的可控性(此处的“控制系统的可控性”就是指控制系统的精确可控性),后来有许多学者考虑Banach空间中微分系统的可控性。但是,文献 [2] [3] 指出:在无穷维抽象空间中,如果算子半群是紧半群,且控制函数满足某些有界性条件,那么抽象微分方程解的精确可控性的结论只能在有限维空间中成立。因此,近年来,一些学者在非紧半群条件下,运用非紧性测度估计技巧及相应的不动点定理讨论了微分系统或微分包含的精确可控性,参见文献 [4] [5] [6]。但是,关于带有积分边界条件的分数阶抽象发展方程的研究比较少 [7] [8],尤其是对由这类方程描述的控制系统的精确可控性的研究结果更为鲜见。
受上述工作的启发,本文在较弱的“紧型”条件和非紧性测度条件下,当A生成一致有界的等度连续半群时,运用Sadovskii不动点定理讨论了带积分边界条件的分数阶发展系统(1)的精确可控性。需要特别指出的是,本文采用了与现有文献不同的方法证明了分数阶发展方程(1)的精确可控性,即在假设了相应的线性系统是精确可控的条件下,证明了分数阶发展方程(1)的精确可控性,此方法详见文献 [6] [9]。
2. 预备知识
设X为Banach空间,其范数为
。又设
为定义于I取值于X的连续函数之集,按范数
构成Banach空间,本文记N为正整数集。
下列关于分数阶微积分的概念参见文献 [10]。
定义2.1 区间I上的函数f的
阶分数阶积分定义为
,
,
其中
是Gamma函数。
定义2.2 区间I上的函数f的
阶Riemann-Liouville型分数阶导数定义为
,
,
其中
表示大于或者等于q的最小整数。
定义2.3 区间I上的函数f的
阶Caputo型分数阶导数定义为
,
,
其中
。
注2.1 (I) Riemamn-Liouville型分数阶导数和Caputo型分数阶导数有下列关系:
.
(II) 常数的Caputo型导数为0。
(III) 如果f是X中的抽象函数,则定义2.1,2.2,2.3中的积分为Bochner意义下的积分。
由文献 [11] 的引理3.1可知,控制系统(1) mild解的定义如下:
定义 2.4 [11] 如果函数
满足下列积分方程
,
,
则称x是控制系统(1)的mild解,其中
;
;
;
,
,
这里 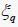 是定义在
上的单边概率密度函数,且
,
。
是定义在
上的单边概率密度函数,且
,
。
引理 2.1 [11] 对任意给定的
,
,
是有界线性算子,即对
,有
,
,
其中
,
。
下面给出精确可控的概念及相关结论:
定义2.5 [6] [9] (精确可控性) 若对任一给定的
,存在控制函数
,使得系统(1)的mild解x满足
,
则称控制系统(1)在区间I上是精确可控的。
首先考虑相应的分数阶线性微分方程
(2)
定义方程(2)的控制算子如下:
,
其中
,
分别是B,
的共轭算子。显然
是线性算子。
设
为系统(2)相应于控制函数u和初值
在右端点
处的状态值,记
,
称
为系统(2)的可达集。
引理2.2 [9] 若
,
则称线性系统(2)在区间I上精确可控。换而言之,如果对给定的终状态值
,存在控制函数
,使得线性系统(2)的mild解x满足
,
则称系统(2)在区间I上精确可控。
引理 2.3 [9] 若线性方程(2)精确可控,则
存在,且存在
,使得
,
.
引理 2.3蕴含了
。
下面我们给出一些关于非紧性测度的概念和结论,这些结论将在后续证明中用到。设X是Banach空间,
是非空有界集。令
,
其中
表示
的直径,则称
为X中D的Kuratowski非紧性测度。显然,
,
表示
中D的Kuratowski非紧性测度。
引理2.4 [12] 设X为Banach空间,
非空有界集,则有
(i)
当且仅当
是相对紧集;
(ii) 若
,则
;
(iii)
。
引理 2.5 [13] 设X为Banach空间,若
为有界且等度连续集,则
在I上连续,且
.
引理2.6 [14] 设X为Banach空间,
为可列集,若存在
,使得
,
,
,则
在I上Lebesgae可积,且
.
引理2.7 [15] 设X是Banach空间,
有界,则存在可列集
,使得
.
定义2.6 [16] 设X是Banach空间,
连续,如果对任意
有界集,满足下列不等式
,
则称A是凝聚映射。
引理2.8 [16] (Sadovskii定理) 设X为Banach空间,
为有界凸闭集,
为凝聚映射,则A在D中至少有一个不动点。
为了证明主要结论,我们给出下列假设条件:
(H1) 线性方程(2)在区间I上精确可控。
(H2)
是连续函数,对
,
,
,使得
.
(H3)
是连续函数,
,使得
,
,
.
(H4) 对
,
,
,集合
在X中相对紧,其中
为任意有界集,
.
3. 主要结果及其证明
对
,取
中非空有界闭凸集
.
根据假设条件,对
,定义控制函数如下:
, (3)
其中
,
.
引理3.1 对
及
,有
,
其中
。
证明:利用引理2.1,引理2.3,以及假设条件(H2),(H3),通过直接计算即可得所求结论,因此我们在此省略细节。
如果
是控制系统(1)相应于控制函数u的mild解。则由定义2.4可知,
,
.
当
时,由(3)式,有
故控制系统(1)在I上精确可控。
因此,要证明控制系统(1)精确可控,只需证明控制系统(1)存在相应于控制函数u的mild解。接下来,我们根据假设条件,运用Sadovskii不动点定理证明控制系统(1) mild解的存在性。
定理3.1 设条件(H1)~(H4)满足。如果不等式
(4)
成立,则方程(1)在区间I上精确可控。
证明:定义算子
,如下:
.
要证明方程(1)在区间I上精确可控,只需要利用上面控制函数证明算子F有不动点。
首先证明:存在
,使得
。反设不真,则对
,存在
,使得对
,有
。由假设条件(H2),(H3)及引理2.1,引理2.3,引理3.1可知,对
,有
两边同除以k并且当
时取极限可得,
,
这与(4)式矛盾,因此存在
,使得
。故
。
接下来,在
上定义算子
和
,
则对
,
,
。
先证明
是压缩映射。因为对 ,结合条件(H2)可知,
,结合条件(H2)可知,
.
由(4)式知,
。所以,
在
上是压缩映射。
再证明
在
上是全连续映射。因为
显然是连续算子,所以仅需证明
是相对紧集。对
,定义
和
。根据Ascoli-Arela定理,只需证明集合W在
中等度连续,
在X中相对紧。首先证明集合W等度连续。对
,满足
及
,有
其中
;
;
.
因为
,
.
又对
,有
.
所以,当
时,
。所以集合W等度连续。
再证明对
,集合
在X中相对紧。显然当
时,
在X中相对紧,因此只需考虑
。对
,
定义
,
其中
.
由条件(H4)可知,集合
在X中相对紧。又因为
.
所以,当
时,存在一个相对紧集
任意接近于
,故集合
在X中相对紧。综上所述,对
,集合
在X中相对紧。因此,由Ascoli-Arela定理可知,
是相对紧集。由引理2.4的(i)知,
。又因为
是压缩的,则
,故由引理2.4的(iii),有
.
所以,由定义2.6知,F是凝聚映射。由Sadovskii不动点定理(见引理2.8)可知,算子F在
上有不动点
。该不动点即为系统(1)的mild解且满足
。故系统(1)在I上精确可控。证毕。
因为条件(H4)在应用中不易验证,所以我们假设
满足如下应用比较广泛的非紧性测度条件:
(H5) 对
,
为非空有界集,存在常数
,使得
.
则可得系统(1)的如下可控性结果:
定理3.2 设条件(H1)~(H3)及条件(H5)满足。如果不等式条件(4)及
(5)
成立,则系统(1)在区间I上精确可控。
证明:由定理3.1的证明可知,存在
,使得
。下面利用条件(H5)证明算子
是凝聚映射。由引理2.7,取
,使得
. (6)
由非紧性测度的性质及假设条件(H2)可知,
其中
为非空有界集。
对
,因为
,
其中
.
所以,对
,有
.
由条件(H5)及引理2.6,对
,有
.
所以,由(6)式和引理2.5可得
.
因此,由(5)式可知,
。所以,由定义2.6知,算子F是凝聚映射。由Sadovskii不动点定理可知,算子F在
上有不动点
。该不动点即为系统(1)的mild解且满足
。故系统(1)在I上精确可控。证毕。
注3.1 定理3.1和定理3.2都只要求
生成的半群
是等度连续半群,没有假设半群的紧性。因此,我们对非线性项附加了“紧型”条件(H4)或者非紧性测度条件(H5)来保证解算子的紧性。进而利用凝聚映射的不动点定理证明了控制系统(1)的mild解的存在性。
注3.2 如果非线性项是有界函数,或者满足一次增长条件,即
,其中
是常数,则条件(H3)自然成立。
例 考虑下列分数阶偏微分系统
(7)
其中
是
阶Caputo型分数阶导数,
,
为有恰当定义的函数。
取状态空间
,
。设
,
,
。作X中的算子A和B:
,
,
则系统(7)可化为形如问题(1)的分数阶发展方程控制系统。由文献 [6],A生成X中的等度连续半群
。
若系统(7)满足条件(H1)~(H4),则按照定理3.1,系统(7)在区间I上精确可控。
NOTES
*通讯作者。