具有混合切换的随机丙型肝炎病毒感染模型的长期性行为

Long Time Behavior of Stochastic Hepatitis C Virus Infection Model with Mixed Switching

摘要: 本文主要研究具有混合切换的随机丙型肝炎病毒感染模型(HCV模型)的灭绝性和持久性。首先，证明了随机HCV模型解的存在性唯一性。其次，利用费勒性质、不变控制集和Krylov-Bogoliubov定理等理论，证明了随机HCV模型的不变概率测度的存在唯一性。最后，运用强遍历性定理、波莱尔康特立引理和迭代对数定律等理论，获得了随机HCV模型的灭绝性和持久性的条件。

Abstract: This paper mainly studies the extinction and persistence of a stochastic hepatitis C virus infection model (HCV model) with mixed switching. First, we prove the existence and uniqueness of the so-lution of the stochastic HCV model. Secondly, we prove the existence and uniqueness of the invariant probability measure of the stochastic HCV model by using the theory of Feller property, invariant control set and Krylov Bogoliubov theorem. Finally, by using the strong ergodicity theorem, Borel-Cantelli lemma and iterated logarithm law, the conditions of extinction and persistence of the stochastic HCV model are obtained.

1. 引言

近年来，全世界持续感染丙型肝炎病毒(HCV)，并有罹患慢性肝病，肝硬化和肝细胞癌风险的人口数量逐步增加。由此，丙型肝炎病毒感染已成为一个严重的全球公共卫生问题，备受关注 [1] - [8]。

最早的丙型肝炎病毒感染模型(HCV模型)是由诺伊曼等人提出 [1]，具体模型如下

$\{\begin{array}{l}\frac{\text{d}{W}_t}{\text{d}t}=S+a{W}_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)-b{W}_t-\left(1-\eta \right)\beta V_t{W}_t+q{I}_t\\ \frac{\text{d}{I}_t}{\text{d}t}=\nu I_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)+\left(1-\eta \right)\beta V_t{W}_t-\omega I_t-q{I}_t\\ \frac{\text{d}{V}_t}{\text{d}t}=\left(1-ϵ\right)p{I}_t-c{V}_t,\end{array}$ (1.1)

其中 $W_t\mathrm{,}{I}_t\mathrm{,}{V}_t$ 分别为t时刻的未感染肝细胞数量，感染肝细胞量和病毒载量，且 $N_t=W_t+I_t+V_t$ 表示细胞总数。S表示未感染的肝细胞可能通过移行或分化成肝细胞前体细胞，以S的构成率增加数量；a表示感染细胞的最大增值速率；b表示未感染细胞的死亡率； $\eta$ 表示使用抗病毒药物治疗所降低的感染率；q表示通过非细胞溶解过程自发治愈感染的肝细胞的治愈率； $\nu$ 表示未感染细胞的最大增值速率； $\beta$ 表示肝细胞游离病毒感染率； $\omega$ 表示感染病毒细胞死亡率； $ϵ$ 表示病毒生产率；p表示细胞产生游离病毒的速率；c表示清除游离病毒的速率。

本文考虑以下三个具有混合切换的随机丙型肝炎病毒感染模型的动力学性质。

模型一：与状态无关的马尔科夫状态切换HCV模型

$\{\begin{array}{l}\frac{\text{d}{W}_t}{\text{d}t}=S_{{\alpha }_t}+a_{{\alpha }_t}{W}_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)-b_{{\alpha }_t}{W}_t-\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t+q_{{\alpha }_t}{I}_t,\\ \frac{\text{d}{I}_t}{\text{d}t}={\nu }_{{\alpha }_t}{I}_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)+\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t-{\omega }_{{\alpha }_t}{I}_t-q_{{\alpha }_t}{I}_t,\\ \frac{\text{d}{V}_t}{\text{d}t}=\left(1-{ϵ}_{{\alpha }_t}\right)p_{{\alpha }_t}{I}_t-c_{{\alpha }_t}{V}_t,\end{array}$ (1.2)

其初始值 $\left(W_t,I_t,V_t\right)=\left(w_0,i_0,v_0\right)\in {ℝ}_{+}^3:=\left(x,y,z\right)\in {ℝ}^3:x>0,y>0,z>0$，对于实数 $M<\infty$，有 ${\alpha }_0=a_0\in \mathcal{M}=\left\{\mathrm{1,2,}\cdots \mathrm{,}M\right\}$。因此， ${\left({\alpha }_t\right)}_{t\ge 0}$ 是一个具有状态空间 $\mathcal{M}$ 的连续时间马尔科夫链，且其具有如下转移概率

$\mathbb{P}\left({\alpha }_{t+\Delta }=j|{\alpha }_t=i\right)=\{\begin{array}{ll}{q}_{ij}\Delta +o\left(\Delta \right),\hfill & i\ne j,\hfill \\ 1+q_{ii}\Delta +o\left(\Delta \right),\hfill & i=j,\hfill \end{array}$ (1.3)

其中 $\Delta \downarrow 0$，且Q-矩阵 $Q={\left(q_{ij}\right)}_{i\mathrm{,}j\in \mathcal{M}}$ ； $a_i\mathrm{,}{b}_i\mathrm{,}{\eta }_i\mathrm{,}{\beta }_i\mathrm{,}{q}_i\mathrm{,}{\nu }_i\mathrm{,}{\epsilon }_i\mathrm{,}{p}_i\mathrm{,}{c}_i>\mathrm{0,}i\in \mathcal{M}$。

模型二：仍然是模型(1.2)，但此时 ${\left({\alpha }_t\right)}_{t\ge 0}$ 是一个具有状态空间 $\mathcal{M}$ 的跳跃过程，对任意 $i\mathrm{,}j\in \mathcal{M}$ 和 $x\in {ℝ}_{+}^3$，其过渡内核如下所示

$\mathbb{P}\left({\alpha }_{t+\Delta }=j\mathrm{<mo>\; |\; </mo>}{\alpha }_t=i\mathrm{,}{X}_t=x\right)=\{\begin{array}{ll}{q}_{ij}\left(x\right)\Delta +o\left(\Delta \right)\mathrm{,}\hfill & i\ne j\mathrm{,}\hfill \\ 1+q_{ii}\left(x\right)\Delta +o\left(\Delta \right)\mathrm{,}\hfill & i=j\mathrm{,}\hfill \end{array}$ (1.4)

无论何时，都有 $\Delta \downarrow 0$，其中 $X_t=\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\right)\in {ℝ}_{+}^3$。

模型三：考虑到依赖于状态的随机环境和随机扰动的影响，随机HCV模型如下

$\{\begin{array}{l}\text{d}{W}_t=\left\{S_{{\alpha }_t}+a_{{\alpha }_t}{W}_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)-b_{{\alpha }_t}{W}_t-\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t+q_{{\alpha }_t}{I}_t\right\}\text{d}t,\\ -\left(b_{{\alpha }_t}^e-a_{{\alpha }_t}^e\right)W_t\text{d}{B}_t^{\left(1\right)}-\frac{a_{{\alpha }_t}^e{I}_t}{W_{\max }}{W}_t\text{d}{B}_t^{\left(2\right)}-\left(1-{\eta }_{{\alpha }_t}^e\right){\beta }_{{\alpha }_t}^e{V}_t{W}_t\text{d}{B}_t^{\left(3\right)},\\ \text{d}{I}_t=\left\{{\nu }_{{\alpha }_t}{I}_t\left(1-\frac{W_t+I_t}{W_{\max }}\right)+\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t-{\omega }_{{\alpha }_t}{I}_t-q_{{\alpha }_t}{I}_t\right\}\text{d}t,\\ -\left({\omega }_{{\alpha }_t}^e+q_{{\alpha }_t}^e-{\nu }_{{\alpha }_t}^e\right)I_t\text{d}{B}_t^{\left(1\right)}-\frac{{\nu }_{{\alpha }_t}^e{W}_t}{W_{\max }}{I}_t\text{d}{B}_t^{\left(2\right)},\\ \text{d}{V}_t=\left\{\left(1-{ϵ}_{{\alpha }_t}\right)p_{{\alpha }_t}{I}_t-c_{{\alpha }_t}{V}_t\right\}\text{d}t-c_{{\alpha }_t}^e{V}_t\text{d}{B}_t^{\left(1\right)}\end{array}$ (1.5)

2. 具有独立于状态的随机HCV模型的灭绝性与持久性

在随机HCV模型(1.2)和(1.3)中，连续时间马尔科夫链 ${\left({\alpha }_t\right)}_{t\ge 0}$ 的转移概率与状态无关。令 $\stackrel{⌣}{S}=ma{x}_{i\in \mathcal{M}}{S}_i$， $\hat{S}=mi{n}_{i\in \mathcal{M}}{S}_i$，其他变量 $\stackrel{⌣}{a}\mathrm{,}\hat{a}\mathrm{,}\stackrel{⌣}{b}\mathrm{,}\hat{b}\mathrm{,}\cdots$ 的定义与它类似。假设

· ${\mathcal{H}}_1$ 对所有的 $i\in \mathcal{M}$， $F\left(\cdot \mathrm{,}i\right)\mathrm{<mo>\; :\; </mo>}ℝ\to {ℝ}_{+}$ 是局部利普希茨连续的，且存在常数 $c>0$，使得 $F\left(x\mathrm{,}i\right)\le c\left(1+\left|x\right|\right)\mathrm{,}x\in ℝ$ ；

· ${\mathcal{H}}_2$ 连续时间马尔科夫链 ${\left({\alpha }_t\right)}_{t\ge 0}$ 是不可约和正递归的，且其具有不变概率测度 $\pi =\left({\pi }_1\mathrm{,}{\pi }_2\mathrm{,}\cdots \mathrm{,}{\pi }_M\right)$。

下面的引理表明，随机HCV模型(1.2)和(1.3)的唯一解在正象限中，并揭示了肝细胞的总数量有一个上界。

引理2.1 假设 ${\mathcal{H}}_1$ 成立，令 $F\left(x\mathrm{,}i\right)=\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t$。则随机丙型肝炎病毒感染模型(1.2)和(1.3) 有唯一强解 $\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\right)\in {ℝ}_{+}^3$，其解的初始值 $\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\right)\in {ℝ}_{+}^3$。此外，仍有

$N_t\le N_0{\text{e}}^{-{\displaystyle {\int }_0^t}{\Upsilon }_{{\alpha }_s}\text{d}s}+{\displaystyle {\int }_0^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s\mathrm{,}\text{a}\text{.s}\mathrm{.}$ (2.1)

Proof. 首先由随机模型(1.2)可以得到

$\begin{array}{l}\text{d}{N}_t=\{S_{{\alpha }_t}-\left(b_{{\alpha }_t}-a_{{\alpha }_t}\right)W_t-\left({\omega }_{{\alpha }_t}-{\nu }_{{\alpha }_t}\right)I_t-\left(W_t+I_t\right)\frac{b_{{\alpha }_t}{W}_t+a_{{\alpha }_t}{I}_t}{W_{\max }}\\ \begin{array}{c}\\ \end{array}+\left(1-{ϵ}_{{\alpha }_t}\right)p_{{\alpha }_t}{I}_t-c_{{\alpha }_t}{V}_t\}\text{d}t,t>0.\end{array}$ (2.2)

又因为 $W_t\mathrm{,}{I}_t\ge 0$，故有

$\text{d}{N}_t\le \left\{S_{{\alpha }_t}-\left(b_{{\alpha }_t}-a_{{\alpha }_t}\right)W_t-\left({\omega }_{{\alpha }_t}-{\nu }_{{\alpha }_t}\right)I_t+\left(1-{ϵ}_{{\alpha }_t}\right)p_{{\alpha }_t}{I}_t-c_{{\alpha }_t}{V}_t\right\}\text{d}t\mathrm{.}$ (2.3)

令 ${\Upsilon }_{{\alpha }_t}\mathrm{<mo>\; =\; </mo>}min\left\{b_{{\alpha }_t}-a_{{\alpha }_t}\mathrm{,}{\omega }_{{\alpha }_t}-{\nu }_{{\alpha }_t}-p_{{\alpha }_t}+{ϵ}_{{\alpha }_t}{p}_{{\alpha }_t}\mathrm{,}{c}_{{\alpha }_t}\right\}$，则有

$\text{d}{N}_t\le \left\{S_{{\alpha }_t}-{\Upsilon }_{{\alpha }_t}{N}_t\right\}\text{d}t\mathrm{.}$

特别地

$\text{d}{N}_t\le \left\{S_{{\alpha }_{{\tau }_k}}-{\Upsilon }_{{\alpha }_{{\tau }_k}}{N}_t\right\}\text{d}t\mathrm{,}t\in \left[{\tau }_k\mathrm{,}{\tau }_{k+1}\right)\mathrm{,}k\in \mathbb{N}\mathrm{.}$

对 $\text{d}\left({\text{e}}^{{\Upsilon }_{{\alpha }_{{\tau }_k}}t}{N}_t\right)$ 应用伊藤链式法，有

$\text{d}\left({\text{e}}^{{\Upsilon }_{{\alpha }_{{\tau }_k}}t}{N}_t\right)={\Upsilon }_{{\alpha }_{{\tau }_k}}{\text{e}}^{{\Upsilon }_{{\alpha }_{{\tau }_k}}t}{N}_t\text{d}t+{\text{e}}^{{\Upsilon }_{{\alpha }_{{\tau }_k}}t}\text{d}{N}_t\le {\text{e}}^{{\Upsilon }_{{\alpha }_{{\tau }_k}}t}{S}_{{\alpha }_{{\tau }_k}}\text{d}t\mathrm{,}$

从而，获得

$\begin{array}{c}{N}_t\le {\text{e}}^{-{\Upsilon }_{{\alpha }_{{\tau }_k}}\left(t-{\tau }_k\right)}{N}_{{\tau }_k}+{\displaystyle {\int }_{{\tau }_k}^t}{S}_{{\alpha }_s}{\text{e}}^{-{\Upsilon }_{{\alpha }_{{\tau }_k}}\left(t-s\right)}\text{d}s={\text{e}}^{-{\displaystyle {\int }_{{\tau }_k}^t}{\Upsilon }_{{\alpha }_s}\text{d}s}{N}_{{\tau }_k}+{\displaystyle {\int }_{{\tau }_k}^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s\\ \le {\text{e}}^{-{\displaystyle {\int }_{{\tau }_k}^t}{\Upsilon }_{{\alpha }_s}\text{d}s}\left({\text{e}}^{-{\displaystyle {\int }_{{\tau }_{k-1}}^t}{\Upsilon }_{{\alpha }_s}\text{d}s}{N}_{{\tau }_{k-1}}+{\displaystyle {\int }_{{\tau }_{k-1}}^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s\right)+{\displaystyle {\int }_{{\tau }_k}^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s\\ ={\text{e}}^{-{\displaystyle {\int }_{{\tau }_{k-1}}^t}{\Upsilon }_{{\alpha }_s}\text{d}s}{N}_{{\tau }_{k-1}}+{\displaystyle {\int }_{{\tau }_{k-1}}^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s\le \cdots \le {\text{e}}^{-{\displaystyle {\int }_0^t}{\Upsilon }_{{\alpha }_s}\text{d}s}{N}_0+{\displaystyle {\int }_0^t}{S}_{{\alpha }_s}{\text{e}}^{-{\displaystyle {\int }_s^t}{\Upsilon }_{{\alpha }_u}\text{d}u}\text{d}s.\end{array}$ (2.4)

引理证明完毕。

推论2.2 假设 ${\mathcal{H}}_1$ 成立，则随机丙型肝炎病毒感染系统(1.2)的解 ${\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\mathrm{,}{\alpha }_t\right)}_{t\ge 0}$ 具有不变概率测度。

证明：首先注意到 ${\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\mathrm{,}{\alpha }_t\right)}_{t\ge 0}$ 是一个费勒过程。由(2.1)式，可得

$W_t\le N_t\le N_0{\text{e}}^{-\hat{\Upsilon }t}+\stackrel{⌣}{S}/\hat{\Upsilon }\mathrm{.}$ (2.5)

对任意 $K>0$，令 $B_K\left(0\right)=\left\{\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\right)\in {ℝ}_{+}^3\mathrm{<mo>\; :\; </mo>}{w}_0+i_0+v_0\le K\right\}$， $M_t\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\mathrm{,}i\mathrm{<mo>\; ;\; </mo>}\cdot \right)$ 是起始点为 $\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\mathrm{,}i\right)\in {ℝ}_{+}^3\times \mathcal{M}$ 的 $\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\mathrm{,}{\alpha }_t\right)$ 的过渡内核。对任意 $t>0$ 和 $\xi \in \mathcal{B}\left({ℝ}_{+}^3\times \mathcal{M}\right)$，定义概率测度

${\chi }_t\left(\xi \right)=\frac{1}{t}{\displaystyle {\int }_0^t}{M}_s\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\mathrm{,}i\mathrm{<mo>\; ;\; </mo>}\xi \right)\text{d}s\mathrm{.}$

则对任意的 $\epsilon >0$，由切比雪夫不等式和(2.5)可知，存在充分大的 $K>0$，使得

${\chi }_t\left(B_K\left(0\right)\times \mathcal{M}\right)=\frac{1}{t}{\displaystyle {\int }_0^t}{M}_s\left(w_0\mathrm{,}{i}_0\mathrm{,}{v}_0\mathrm{,}i\mathrm{<mo>\; ;\; </mo>}{B}_K\left(0\right)\text{d}s\times \mathcal{M}\right)\ge 1-\frac{1}{K}\underset{t\ge 0}{sup}E{N}_t\ge 1-\epsilon \mathrm{.}$

因为 $B_K\left(0\right)$ 是 ${ℝ}_{+}^3$ 的紧子集，所以， ${\left({\chi }_t\right)}_{t\ge 0}$ 是紧的。由Krylov-Bogoliubov’s定理 [9] [10] 可知， ${\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\mathrm{,}{\alpha }_t\right)}_{t\ge 0}$ 具有不变概率测度。推论证明完毕。

定理2.3 假设 ${\mathcal{H}}_1$ 和 ${\mathcal{H}}_2$ 成立，并进一步假设存在具有 $li{m}_{t\to \infty }{\Psi }_t=0$ 的 $\Psi$ ： $\left[\mathrm{0,}\infty \right)\to \left[\mathrm{0,}\infty \right)$ 和 $\Phi \mathrm{<mo>\; :\; </mo>}\mathcal{M}\to \left[\mathrm{0,}\infty \right)$ 使得

$\frac{\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t}{I_t}\le {\Psi }_t+{\Phi }_{{\alpha }_t}$ (2.6)

和

${\Delta }_1:=\frac{{\displaystyle {\sum }_{i\in \mathcal{M}}{\pi }_i{\Phi }_i}}{{\displaystyle {\sum }_{i\in \mathcal{M}}{\pi }_i\left({\omega }_i+q_i-{\nu }_i\right)}}<1.$ (2.7)

则有

$\underset{t\to \infty }{lim}{I}_t=\mathrm{0,}\text{a}\text{.s}\mathrm{.,}\underset{t\to \infty }{lim}{V}_t=\mathrm{0,}\text{a}\text{.s}\mathrm{.}$ (2.8)

和

$\frac{1}{t}{\displaystyle {\int }_0^t}\left\{\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\right\}\text{d}s={\displaystyle \underset{i\in \mathcal{M}}{\sum }}{\pi }_i{S}_i\mathrm{.}$ (2.9)

证明：设 $\left(W_t\mathrm{,}{I}_t\mathrm{,}{V}_t\right)\in {\left({ℝ}_{+}\right)}^3$，由(1.2)和(2.6)，可得

$\begin{array}{c}\frac{\text{d}}{\text{d}t}\ln I_t={\nu }_{{\alpha }_t}\left(1-\frac{W+I}{W_m}\right)+\frac{\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t}{I_t}-{\omega }_{{\alpha }_t}-q_{{\alpha }_t}\\ =-\frac{{\nu }_{{\alpha }_t}\left(W_t+I_t\right)}{W_m}+\frac{\left(1-\eta \right){\beta }_{{\alpha }_t}{V}_t{W}_t}{I_t}+{\nu }_{{\alpha }_t}-{\omega }_{{\alpha }_t}-q_{{\alpha }_t}\\ \le \frac{\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t}{I_t}-\left({\omega }_{{\alpha }_t}+q_{{\alpha }_t}-{\nu }_{{\alpha }_t}\right)\\ \le {\Psi }_t+{\Phi }_t-\left({\omega }_{{\alpha }_t}+q_{{\alpha }_t}-{\nu }_{{\alpha }_t}\right).\end{array}$ (2.10)

从而，获得

$ln\left(\frac{I_t}{I_0}\right)\le {\displaystyle {\int }_0^t}{\Psi }_s\text{d}s+{\displaystyle {\int }_0^t}\left({\Phi }_s-\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)\right)\text{d}s\mathrm{.}$ (2.11)

因此，利用马氏链的强遍历性定理，除了有 $li{m}_{t\to \infty }{\Psi }_t=0$ 之外，还获得

$\underset{t\to \infty }{\lim }\sup \frac{\ln I_t}{t}\le {\displaystyle \underset{i\in \mathcal{M}}{\sum }}\left\{{\Phi }_i-\left({\omega }_i+q_i-{\nu }_i\right)\right\}{\pi }_i,\text{a}\text{.s}.$

因此，有 $li{m}_{t\to \infty }{I}_t=0$，a.s.

下证 $li{m}_{t\to \infty }{V}_t=0$，a.s.，注意到

$\text{d}{V}_t\le \left\{\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{I}_t-\hat{v}{V}_t\right\}\text{d}t\mathrm{,}$

对 $\text{d}\left({\text{e}}^{ct}{V}_t\right)$ 应用伊藤链式法，有

$V_t\le V_0{\text{e}}^{-\hat{c}t}+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_0^t}{\text{e}}^{-\hat{c}\left(t-s\right)}{I}_s\text{d}s$ (2.12)

又因为 $li{m}_{t\to \infty }{I}_t=0$，a.s.，所以对任意 $\epsilon >0$，存在具有 $\mathbb{P}\left({\Omega }_0\right)=1$ 的 ${\Omega }_0\subseteq \Omega$ 和 $T=T\left(\omega \right)>0$，使得

$I_t\left(\omega \right)\le \frac{\hat{c}\epsilon }{3\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}}\mathrm{,}t\ge T\mathrm{,}\omega \in {\Omega }_0\mathrm{.}$

这就意味着

$\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_T^t}{\text{e}}^{-\hat{c}\left(t-s\right)}{I}_s\left(\omega \right)\text{d}s\le \frac{\epsilon }{3}\mathrm{,}\omega \in {\Omega }_0\mathrm{,}t\ge T\mathrm{.}$

结合(2.12)式可得：只要

$t\ge T\vee \left(\frac{1}{\hat{c}}ln\frac{3V_0}{\epsilon }\right)\vee \left(T+\frac{1}{\hat{c}}ln\frac{3\left(1-\widehat{ϵ}\right)\left(N_0+\frac{\stackrel{⌣}{S}}{\hat{\gamma }}\right)}{\hat{c}\epsilon }\right)\mathrm{,}$

就有

$\begin{array}{c}{V}_t\left(\omega \right)\le V_0{\text{e}}^{-\hat{c}t}+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_0^T}{\text{e}}^{-\hat{c}\left(t-s\right)}{I}_s\left(\omega \right)\text{d}s+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_T^t}{\text{e}}^{-\hat{c}\left(t-s\right)}{I}_s\left(\omega \right)\text{d}s\\ \le \frac{\epsilon }{3}+V_0{\text{e}}^{-\hat{c}t}+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_0^T}{\text{e}}^{-\hat{c}\left(t-s\right)}{I}_s\left(\omega \right)\text{d}s\\ \le \frac{\epsilon }{3}+V_0{\text{e}}^{-\hat{c}t}+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}\left(N_0+\frac{\stackrel{⌣}{S}}{\hat{\gamma }}\right){\displaystyle {\int }_0^T}{\text{e}}^{-\hat{c}\left(t-s\right)}\text{d}s\\ \le \epsilon \mathrm{,}\omega \in {\Omega }_0\mathrm{.}\end{array}$ (2.13)

由此证得 $li{m}_{t\to \infty }{V}_t=0$，a.s.

根据(2.8)有

$\underset{t\to \infty }{lim}\left(\frac{1}{t}{\displaystyle {\int }_0^t}{I}_s\text{d}s\right)=\mathrm{0,}\text{a}\text{.s}\text{.}\underset{t\to \infty }{lim}\left(\frac{1}{t}{\displaystyle {\int }_0^t}{V}_s\text{d}s\right)=\mathrm{0,}\text{a}\text{.s}\mathrm{.}$ (2.14)

由(2.2)可以得到下式

$\begin{array}{l}\frac{1}{t}\{{\displaystyle {\int }_0^t}\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\wedge 2)\end{array}$ 之间，通过BDG不等式和(4.1)式可知，存在常数

${\tilde{M}}_p,{\hat{M}}_p>0$，使得

$\begin{array}{c}E\left(\underset{t\in \left[k,k+1\right]}{\sup }{\left|{\displaystyle {\int }_k^t}\frac{{\nu }_{{\alpha }_s}^e{W}_s}{W_{\max }}\text{d}{B}_s^{\left(2\right)}\right|}^p\right)\le {\tilde{M}}_p\frac{{\stackrel{⌣}{\nu }}^e}{W_{\max }}E{\left({\displaystyle {\int }_k^{k+1}}{W}_s^2\text{d}s\right)}^{\frac{p}{2}}\\ \le {\tilde{M}}_p\frac{{\stackrel{⌣}{\nu }}^e}{W_{\max }}E\left(\underset{k\le s\le k+1}{\sup }{W}_s^p\right)\\ \le {\hat{M}}_p.\end{array}$ (4.11)

对任意常数 $C>0$ 和每个实数 $k\ge 1$，令

$B_{k\mathrm{,}C}\mathrm{<mo>\; :\; </mo>}=\left\{\frac{1}{k}\underset{t\in \left[k,k+1\right]}{\sup }\left|{\displaystyle {\int }_k^t}\frac{{\nu }_{{\alpha }_s}^e{W}_s}{W_{\max }}\text{d}{B}_s^{\left(2\right)}\right|\ge C\right\}$

由切比雪夫不等式及(4.11)式，可得

$\mathbb{P}\left(B_{k\mathrm{,}C}\right)\le \frac{1}{k^p{C}^p}E\left(\underset{t\in \left[k\mathrm{,}k+1\right]}{sup}{\left|{\displaystyle {\int }_k^t}\frac{{\nu }_{{\alpha }_s}^e{W}_s}{W_{\max }}\text{d}{B}_s^{\left(2\right)}\right|}^p\right)\le \frac{{\hat{M}}_p}{k^p{C}^p}$

又因为级数 ${\displaystyle {\sum }_{k=1}^{\infty }\frac{1}{k^p}}$ 收敛，于是利用波莱尔—康特立引理，可以得到

$\mathbb{P}\left(\underset{k\to \infty }{\lim }\sup B_{k,C}\right)=0.$

由C的任意性可知(4.9)式成立。

下证(4.10)式成立 令 $z_0=0,z_k={\displaystyle {\int }_0^k}\frac{{\nu }_{{\alpha }_s}{W}_s}{W_{\max }\text{d}{B}_s^{\left(2\right)}},u_k=z_k-z_{k-1},k\ge 1$

显然， $E\left(u_k/k\right)<\infty$，另一方面，(4.11)式意味着

${\displaystyle \underset{k=1}{\overset{\infty }{\sum }}}E\left({\left|u_k\right|}^p|{\mathcal{F}}_{k-1}\right)k^{-p}\le {\hat{M}}_p{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}}{k}^{-p}<\infty$ (4.12)

因此，由( [15], Theorem 5)知，(4.10)式成立。

类似地，可以得到以下结果

$\underset{t\to \infty }{\lim }\frac{1}{t}\left({\displaystyle {\int }_0^t}\left(b_{{\alpha }_t}-a_{{\alpha }_t}\right)W_s\text{d}{B}_s^{\left(1\right)}\right)=0;\underset{t\to \infty }{\lim }\frac{1}{t}\left({\displaystyle {\int }_0^t}\frac{a_{{\alpha }_t}{I}_s}{W_{\max }}\text{d}{B}_s^{\left(2\right)}\right)=0;$ (4.13)

$\underset{t\to \infty }{\lim }\frac{1}{t}\left({\displaystyle {\int }_0^t}\left(1-{\eta }_{{\alpha }_s}\right){\beta }_{{\alpha }_s}{V}_s{W}_s\text{d}{B}_s^{\left(3\right)}\right)=0;\underset{t\to \infty }{\lim }\frac{1}{t}\left({\displaystyle {\int }_0^t}\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)I_s\text{d}{B}_s^{\left(1\right)}\right)=0;$

$\underset{t\to \infty }{\lim }\frac{1}{t}\left({\displaystyle {\int }_0^t}{c}_{{\alpha }_s}{V}_s\text{d}{B}_s^{\left(1\right)}\right)=0;\underset{t\to \infty }{\lim }\frac{N_t}{t}=0;$

定理4.1 假设 ${\mathcal{H}}_1$ 和 ${\mathcal{H}}_2$ 及引理3.1中的条件成立，并进一步假设存在具有 $li{m}_{t\to \infty }{\Psi }_t=0$ 的 $\Psi :\left[\mathrm{0,}\infty \right)\to \left[\mathrm{0,}\infty \right)$ 和 $\Phi \mathrm{<mo>\; :\; </mo>}\mathcal{M}\to \left[\mathrm{0,}\infty \right)$，使得 $\left(1-{\eta }_{{\alpha }_t}\right){\beta }_{{\alpha }_t}{V}_t{W}_t/I_t\le {\Psi }_t+{\Phi }_{{\alpha }_t}$。

(a) 若 $i\mapsto {\Phi }_i^{*}:={\Phi }_i-\left({\omega }_i+q_i-{\nu }_i\right)$ 为非减的，且有

${\Delta }_9:=\frac{{\displaystyle {\sum }_{i\in \mathcal{M}}{\tilde{\pi }}_i{\Phi }_i}}{{\displaystyle {\sum }_{i\in \mathcal{M}}{\tilde{\pi }}_i\left({\omega }_i+q_i-{\nu }_i\right)}}<1.$ (4.14)

则有

$\underset{t\to \infty }{\lim }{I}_t=0,\text{a}\text{.s}.\underset{t\to \infty }{\lim }{V}_t=0,\text{a}\text{.s}\text{.}$ (4.15)

和

$\begin{array}{c}{\displaystyle \underset{i\in \mathcal{M}}{\sum }}{\pi }_i^{\mathrm{<mo>\; *\; </mo>}}{S}_i\le \underset{t\to \infty }{\lim \inf }\left(\frac{1}{t}{\displaystyle {\int }_0^t}\left\{\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\right\}\text{d}s\right)\\ \le \underset{t\to \infty }{\lim \sup }\left(\frac{1}{t}{\displaystyle {\int }_0^t}\left\{\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\right\}\text{d}s\right)\le {\displaystyle \underset{i\in \mathcal{M}}{\sum }}{\tilde{\pi }}_i{S}_i\mathrm{.}\end{array}$ (4.16)

(b) 若 $i\mapsto {\Phi }_i^{\mathrm{<mo>\; *\; </mo>}}\mathrm{<mo>\; :\; </mo>}={\Phi }_i-\left({\omega }_i+q_i-{\nu }_i\right)$ 为非增的，且有

${\Delta }_{10}\mathrm{<mo>\; :\; </mo>}=\frac{{\displaystyle {\sum }_{i\in \mathcal{M}}{\pi }_i^{\mathrm{<mo>\; *\; </mo>}}{\Phi }_i}}{{\displaystyle {\sum }_{i\in \mathcal{M}}{\pi }_i^{\mathrm{<mo>\; *\; </mo>}}\left({\omega }_i+q_i-{\nu }_i\right)}}<1.$ (4.17)

则有

$\underset{t\to \infty }{lim}{I}_t=\mathrm{0,}\text{a}\text{.s}\mathrm{.}d\underset{t\to \infty }{lim}{V}_t=\mathrm{0,}\text{a}\text{.s}\text{.}$

和

$\begin{array}{c}{\displaystyle \underset{i\in \mathcal{M}}{\sum }}{\tilde{\pi }}_i{S}_i\le \underset{t\to \infty }{\lim \inf }\left(\frac{1}{t}{\displaystyle {\int }_0^t}\left\{\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\right\}\text{d}s\right)\\ \le \underset{t\to \infty }{\lim \sup }\left(\frac{1}{t}{\displaystyle {\int }_0^t}\left\{\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\right\}\text{d}s\right)\le {\displaystyle \underset{i\in \mathcal{M}}{\sum }}{\pi }_i^{\mathrm{<mo>\; *\; </mo>}}{S}_i\mathrm{.}\end{array}$ (4.18)

证明：为了使证明更加简化，记

$I_1\left(t\right)=-{\displaystyle {\int }_0^t}{\mu }_{{\alpha }_s}^e\text{d}{B}_s^{\left(1\right)}\mathrm{<mo>\; ;\; </mo>}{I}_2\left(t\right)=-\frac{1}{t}{\displaystyle {\int }_0^t}\frac{{\nu }_{{\alpha }_s}{W}_s}{W_{max}}\text{d}{B}_s^{\left(2\right)}\mathrm{.}$

由伊藤公式及 $0\le W_t\le N_t$，可得

$\begin{array}{l}\frac{1}{t}\ln \left(I_t/I_0\right)\\ =\frac{1}{t}{\displaystyle {\int }_0^t}\{-{\nu }_{{\alpha }_s}\frac{W_s+I_s}{W_{\max }}+\frac{\left(1-{\eta }_{{\alpha }_s}\right){\beta }_{{\alpha }_s}{V}_s{W}_s}{I_s}-\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)-\frac{1}{2}{\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)}^2\\ -\frac{1}{2}{\left(\frac{{\nu }_{{\alpha }_s}{W}_s}{W_{\max }}\right)}^2\}\text{d}s-\frac{1}{t}{\displaystyle {\int }_0^t}\left({\omega }_{{\alpha }_s}^e+q_{{\alpha }_s}^e-{\nu }_{{\alpha }_s}^e\right)\text{d}{B}_s^{\left(1\right)}-\frac{1}{t}{\displaystyle {\int }_0^t}\frac{{\nu }_{{\alpha }_s}{W}_s}{W_{\max }}\text{d}{B}_s^{\left(2\right)}\\ \le \frac{1}{t}{\displaystyle {\int }_0^t}\left\{\frac{\left(1-{\eta }_{{\alpha }_s}\right){\beta }_{{\alpha }_s}{V}_s{W}_s}{I_s}-\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)\right\}\text{d}s+\frac{I_1\left(t\right)}{t}+I_2\left(t\right)\\ \le \frac{1}{t}{\displaystyle {\int }_0^t}\left\{{\Psi }_s+{\Phi }_{{\alpha }_s}-\left({\omega }_{{\alpha }_s}+q_{{\alpha }_s}-{\nu }_{{\alpha }_s}\right)\right\}\text{d}s+\frac{I_1\left(t\right)}{t}+I_2\left(t\right).\end{array}$ (4.19)

由引理4.2知

$\underset{t\to \infty }{lim}{I}_2\left(t\right)=0\text{a}\text{.s}\text{.}$ (4.20)

令 ${\langle I_1\rangle }_t$ 为 $I_1\left(t\right)$ 的二次变差，则有

$\underset{t\to \infty }{\lim \sup }\frac{1}{t}{\langle I_1\rangle }_t\le {\left({\stackrel{⌣}{\mu }}^e\right)}^2\mathrm{.}$

由此，根据连续鞅的强大数定理，可得

$\underset{t\to \infty }{lim}\frac{1}{t}{I}_1\left(t\right)=0\text{a}\text{.s}\text{.}$ (4.21)

结合(4.20)和(4.21)及 $i\mapsto {\Phi }_i^{\mathrm{<mo>\; *\; </mo>}}$ 非降(或非增)的性质，并利用引理3.1和连续时间马尔科夫链的强遍历性定理，即得

$\underset{t\to \infty }{lim}{I}_t=0\text{a}\text{.s}\text{.}$

这意味着对任意 $\epsilon \in \left(\mathrm{0,1}\right)$ 充分小，存在 ${\Omega }_1\subseteq \Omega \left(\mathbb{P}\left({\Omega }_1\right)=1\right)$ 和 $T_1=T_1\left(\omega \right)>0$，使得

$I_t\left(\omega \right)\le \epsilon \mathrm{,}t\ge T_1\mathrm{,}\omega \in {\Omega }_1$ (4.22)

令 ${\xi }_i\mathrm{<mo>\; :\; </mo>}={\omega }_i+{\iota }_i+{\left({\mu }_i^e\right)}^2/2\mathrm{,}i\in \mathcal{M}$，且对任意 $0\le s\le t$，

$S_{s,t}:={\displaystyle {\int }_s^t}{\mu }_{{\alpha }_u}^e\text{d}{B}_u^{\left(2\right)};{\Phi }_{s,t}:=\exp \left(-{\displaystyle {\int }_s^t}{\xi }_{{\alpha }_u}\text{d}u-S_{s,t}\right).$

由(4.21)得

$\underset{t\to \infty }{lim}\frac{1}{t}ln{\Phi }_{\mathrm{0,}t}<\mathrm{0,}\text{a}\text{.s}\text{.}$

这就意味着必定会存在 ${\Omega }_2\subseteq \Omega \left(\mathbb{P}\left({\Omega }_2\right)=1\right)$ 和 $T_2=T_2\left(\omega \right)>0$，使得

${\Phi }_{\mathrm{0,}t}\left(\omega \right)\le \epsilon \mathrm{,}t\ge T_2\mathrm{,}\omega \in {\Omega }_2\mathrm{.}$ (4.23)

而后，利用随机积分的迭代对数定律 [16] [17]，可以得到

$\underset{t\to \infty }{\lim \inf }\frac{S_{s,t}}{\sqrt{2{\langle S\rangle }_{s,t}\log \log {\langle S\rangle }_{s,t}}}=-1\text{a}\text{.s}.$

因此，必定存在 ${\Omega }_3\subseteq \Omega \left(\mathbb{P}\left({\Omega }_3\right)=1\right)$ 和 $T_3=T_3\left(\omega \right)>0$，使得

$-\left(1+\epsilon \right)\sqrt{2{\langle S\rangle }_{s,t}\log \log {\langle S\rangle }_{s,t}}\le S_{s,t}\le \left(-1+\epsilon \right)\sqrt{2{\langle S\rangle }_{s,t}\log \log {\langle S\rangle }_{s,t}},t,s\ge T_2,\epsilon \in {\Omega }_3.$ (4.24)

由常数变易公式，由(4.23)和(4.24)式可知，对任意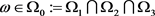和 $t\ge T\mathrm{<mo>\; :\; </mo>}=T_1+T_2+T_3$，

$\begin{array}{c}{V}_t\left(\omega \right)={\Phi }_{0,t}\left(\omega \right)\left\{V_0+{\displaystyle {\int }_0^t}{\Phi }^{-1}\left(s\right)\left(1-{ϵ}_{{\alpha }_s}\right)p_{{\alpha }_s}{I}_s\left(\omega \right)\text{d}s\right\}\\ ={\Phi }_{0,t}\left(\omega \right)V_0+{\Phi }_{s,t}\left(\omega \right){\displaystyle {\int }_0^t}\left(1-{ϵ}_{{\alpha }_s}\right)p_{{\alpha }_s}{I}_s\left(\omega \right)\text{d}s\\ \le V_0\epsilon +{\Phi }_{T,t}\left(\omega \right)\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_0^T}{I}_s\left(\omega \right){\Phi }_{s,T}\left(\omega \right)\text{d}s+\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_T^t}{I}_s\left(\omega \right){\Phi }_{s,t}\left(\omega \right)\text{d}s\\ \le V_0\epsilon +\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}\epsilon {\displaystyle {\int }_T^t}\exp \left(-{\displaystyle {\int }_s^t}{\xi }_{{\alpha }_u}\text{d}u+\left(1+\epsilon \right)\sqrt{2{\langle S\rangle }_{s,t}\log \log {\langle S\rangle }_{s,t}}\right)\text{d}s\\ +\left(1-\widehat{ϵ}\right)\stackrel{⌣}{p}{\displaystyle {\int }_0^T}{I}_s\left(\omega \right){\Phi }_{s,T}\left(\omega \right)\text{d}s\exp \left(-{\displaystyle {\int }_T^t}{\xi }_{{\alpha }_u}\text{d}u+\left(1+\epsilon \right)\sqrt{2{\langle S\rangle }_{T,t}\log \log {\langle S\rangle }_{T,t}}\right).\end{array}$ (4.25)

显然，经观察可知，必定会存在实数 $c>0$ 和 $q\in \left(\mathrm{0,1}\right)$，使得

$\left(1+\epsilon \right)\sqrt{2{\langle S\rangle }_{s,t}\log \log {\langle S\rangle }_{s,t}}\le c+q{\displaystyle {\int }_s^t}{\xi }_{{\alpha }_u}\text{d}u.$ (4.26)

将(4.26)式代入(4.25)式，并由 $\epsilon \in \left(\mathrm{0,1}\right)$ 的任意性，可得(4.15)式成立。

结合(4.15)，根据(4.2)和(4.13)式可得

$\underset{t\to \infty }{lim}\left(\frac{1}{t}{\displaystyle {\int }_0^t}\left\{S_{{\alpha }_s}-\left(b_{{\alpha }_s}-a_{{\alpha }_s}\right)W_s+\frac{b_{{\alpha }_s}{W}_s^2}{W_{\max }}\text{d}s\right\}\right)=0$ (4.27)

结合引理3.1即得(4.16)和(4.18)式。

基金项目

国家自然科学基金(41665006、11561009)，广西自然科学基金(2018GXNSFAA380240)。