1. 引言
Virasoro代数是一类复数域上重要的无限维李代数,其表示理论在共形场论和弦论中有十分重要的应用,其研究方法和结果也促进了大量与之相关的无限维分次李代数的研究,其中对李代数进行形变与推广是产生新代数的一种重要手段。文献 [1] 定义了Virasoro-like李代数
。文献 [2] - [8] 对
进行推广,分别得到了一些相关的Virasoro李代数。余德民等人在文献 [7] 中构造了一类秩为8的Virasoro代数,并对其相关性质进行研究。本文将文献 [7] 从两方面进行推广。一是重新定义李运算构造秩为8的Virasoro代数,二是将其推广至秩为2n的情形,并分别研究两类代数的自同构群及其子群、子代数、单性等相关性质。
2. 秩为8的Virasoro代数
设
为复数域C上的一个线性空间,
,在线性空间V上定义李运算如下:
在基上进行双线性扩张,易验证李运算满足反对称性和雅克比恒等式,故线性空间V关于这个李运算构成一个新的Virasoro代数。
定理2.1 令
,其中
,
为1,2,3,4,5,6,7的一个排列。在P上定义映射乘法
,
,则集合P关于映射乘法构成一个代数,且与
同构。
证明 构造P到
的同构映射
,易得定理成立。
对
,定义以下变换:
,
,
,
,
,
,
并将
在V的基向量上进行线性扩张。
定理2.2 映射
是V的自同构。
证明 令
,
。由于
故
,
,又f2是双射,故f2是V的同构。
同理,
是V的自同构。
定理2.3
关于映射乘法同构于对称群
。
证明 由于三元对称群
。建立
。由于
,
,
同理得
,
,又F为双射,故F为同构映射,即H同构于
。
由定理2.3易得以下推论成立。
推论2.1
,定义以下变换:
,
,
,
,
,
并将
在V的基向量上进行线性扩张。则
关于映射乘法与对称群
同构。
推论2.2 对
,定义以下变换:
,
,
则
关于映射乘法构成一个Klein四元群。
,定义
。显然,
有以下两种特殊情形:
当
时,
,
;当
时,
是同构,记为
,
。
推论2.3
在以上映射乘法的定义下构成一个二阶群。
引理2.1 定义
,
,并将
在V的基向量上线性扩张,则
是V的单自同态。
证明
故对于
,
,易知
为单射,故
是V的单自同态。
显然,
有以下四种特殊情况:
当
,
时,
为恒等同构,即
,
,
当
,
时,
为同构,记为
,
,
当 ,
时,
为同构,记为
,
,
,
时,
为同构,记为
,
,
当
,
时,
为同构,记为
,
。
定理2.4
在以上映射乘法的定义下构成Klein四元群。
证明 由题意得,
,又有
,同理,
,
,
,故
构成Klein四元群。
对该李代数上的子代数进行探讨,得到相关结果如下。
性质2.1 V无中心。
证明 令
,
,
.
假设V有中心
,则对
,有
又由假设及李运算的反对称性,得
。于是
,
,
故
或
,而存在
,有
。
故若
不全为0,存在
,有
.
而
时,
,有
。故V为无中心的Virasoro代数。
性质2.2 设
为
构成的李代数,则
是V的非零真理想,V不是单李代数。
证明 因为
,
有
可以确定
而
。假设
,则一定有
,
显然矛盾。故
是V的非零真理想,V不是单李代数。
由于
,
,易得以下结论。
性质2.3 由
构成的子空间为V的一维交换理想,即V不是半单李代数。
性质2.4 设
,其中矩阵元素均为整数,则由基向量
构成的子空间是V的交换子代数。
证明 由于
则
或
。
若
,则矩阵N中的每个行向量皆是0,故对任意的
都有
,
。故结论成立。
若
,则N的任意一个子矩阵
都满足
或
。故
,即
.
综上,由基向量
生成的子空间是V的交换子代数。
性质2.5 设
是根据基向量
构成的V的线性子空间,则
中不存在二维非交换李子代数。
证明 令 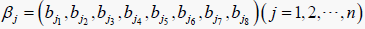 。假设
中存在二维非交换李子代数,那么
。假设
中存在二维非交换李子代数,那么
中有基向量x,y,
。令
,
,
,
,那么x与y已按字典序
排列。由
则
上的极小项为
,极小项系数为
,
而x的极小项为 ,极小项系数为
。
,极小项系数为
。
由
,故
,故
。而由题意
,故
中不存在二维非交换李子代数。
构造7个李代数
。显然它们都是C上线性空间,其基向量都是
。依次作如下定义,
上李运算:
,
上李运算:
,
上李运算:
,
上李运算:
,
上李运算:
,
上李运算:
,
上李运算:
。
定理2.5 代数
都与V同构。
证明
,构造
,
。由于
故
,
,且
是双射,故
为同构映射,V与
同构。
同理,
,定义
,
,
,
,
,
,
则
都为同构映射,即代数
都与V同构。
3. 秩为2n的Virasoro代数
将文献 [7] 基元的秩推广至2n,可得一类新的Virasoro代数如下。
设
为复数域C上一线性空间,基为 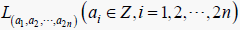 ,在线性空间U上定义李运算如下:
,在线性空间U上定义李运算如下:
在基上双线性扩张,可由定义分别验证该运算满足反对称性和雅克比恒等式,从而得到该线性空间U关于所定义的运算构成一个新的无限维李代数。
定理3.1 令
,
,
,其中
与
分别是
和
的
排列。定义映射乘法为
,
,则
关于映射乘法都构成自同构群,且与对称群
同构。
证明 分别构造 到对称群
的映射:
到对称群
的映射:
,
.
易得
分别是集合
与
之间的同构映射。故
关于映射乘法都构成自同构群,且与对称群
同构。
对于
中元素,
,定义
,
,
,
,
,
其中
,且
,将
分别在U的基向量上线性扩张。
定理3.2
是U的同构。
证明 令
。由
又由
由
,故
,
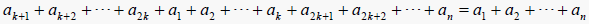 .
.
于是
,
,
,
是同态映射。由于
为双射,故
为U的同构。同理,
都是U的同构。
定理3.3
在关于映射乘法同构于对称群
。
证明 由于
。建立
。由
又由
,
。
同理,可得
, ,又
为双射,故
为同构映射。即
在以上映射乘法的定义下同构于三元对称群
。
,又
为双射,故
为同构映射。即
在以上映射乘法的定义下同构于三元对称群
。
对于
中元素,
,定义
,
,
,
,
.
由定理3.3易得以下推论成立。
推论3.1
关于映射乘法同构于对称群
。
对于
中元素,
,定义
,
.
定理3.4
关于映射乘法构成Klein四元群。
证明 由定义,
.
又有
,同理,得
,
,
。故
构成Klein四元群。
,构造
,
,则
有以下两种特殊情形:
当
时,
是恒等同构,即
,
,
当
时,
是同构,记为
,
。
推论3.2
关于映射乘法构成一个二阶群。
引理3.1
,构造
,则
是U的单自同态。
证明
故有
,
,又
为单射,故
是单自同态。
显然,
有四种特殊情况:
当
,
时,
为恒等同构,即e,
,
当
,
时,
为同构,记为
,
,
当
,
时,
为同构,记为
,
,
当
,
时,
为同构,记为
,
。
定理3.5
关于映射乘法构成Klein四元群。
以下结果与秩为8的代数类似,不再证明。
性质3.1 U无中心。
性质3.2 设
为
构成的李代数。则
是U的非零真理想,U不是单李代数。
性质3.3 由
构成的一维子空间是U的一维交换理想,即U不是半单李代数。
性质3.4设
,其中矩阵元素均为整数,则由
基向量
构成的子空间是U的交换子代数。
基金项目
2018年浙江省高等教育十三五第一批教学改革研究项目“基于超星学习通平台的混合式教学模式研究——以线性代数课程为例”(jg20180248)。
NOTES
*通讯作者。